线性代数复习笔记
线性代数笔记
一些参考来源:
- 武汉大学黄正华老师个人主页 有很多数学相关的有用资料
- 3blue1brown B站账号 数形结合,以可视化的方式展现公式
基向量 basis vectors
v与w全部线性组合构成的向量集合称为“张成的空间”
有多个向量,并且可以移除其中一个而不减小张成的空间,称其为线性相关(Linearly dependent)的
向量空间的一组基是张成该空间的一个线性无关向量集

线性变换 Linear transformation
保持网格线平行且等距分布
将其看作一种对空间挤压变换的函数
- 直线依旧是直线\(L(v+w)=L(v)+L(w)\)
- 原点保持固定\(L(cv)=cL(v)\)
两个矩阵相乘的几何意义是将两个线性变换相继作用,这个乘积需要从右向左读
直观表现矩阵乘法具有结合律
\(A(BC)=(AB)C\)
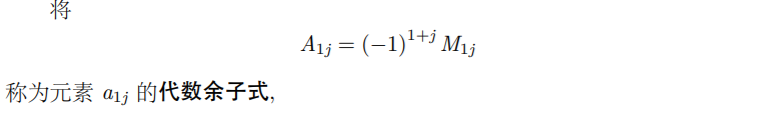
行列式 determinant
对于二维来说,代表线性变换改变面积的比例;对于三维,代表体积的缩放
所以,可以用一个矩阵的行列式是否为0来判断是否将空间压缩到更小的维度上
负的行列式表示空间定向(orientation)发生了改变(flipping),二维中用旋转方向表示,三维中用右手法则表示
n阶行列式

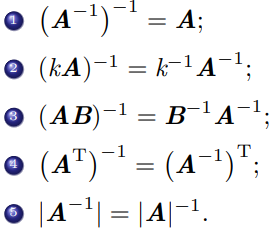
范德蒙行列式

行列式性质
- 行列式转置后值不变,\(D^T=D\)
- 行列式A中某行(或列)用同一数k乘,其结果等于kA
- 互换行列式中两行,值变为相反数
- 行列式某行元素全为0,行列式值为0
- 行列式中两行成比例,行列式为0
- 行列式中一行(或列)所有元素乘以一个数后加到另一行(或列),行列式值不变
- 行列式中一行(或列)可以写成两元素相加形式,可以拆分为两个行列式相加
- ⼀⾏元素乘以另⼀⾏对应元素的代数余⼦式, 其和为零
矩阵运算
A代表一个线性变换,使得向量X变换后与V重合
当\(det(A)\ne0\)时,有唯一解,可以通过逆变换(inverse)来找到X
行列式不为零才有逆矩阵
当\(det(A)=0\)时,可能存在解
奇异矩阵
行列式等于0的方阵
伴随矩阵
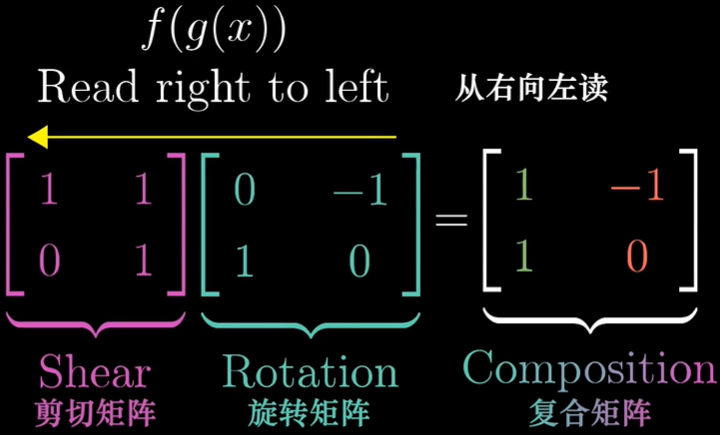
由行列式|A|的代数余子式\(A_{ij}\)所构成的矩阵

可得以下重要公式:
逆矩阵
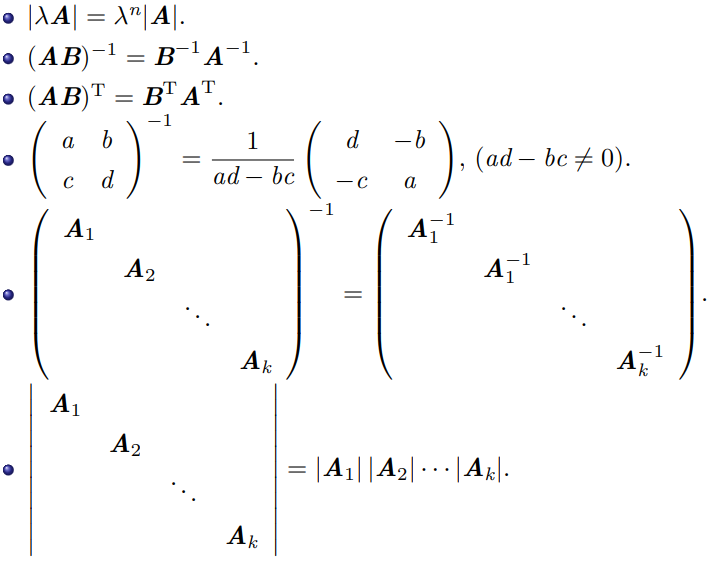
正交矩阵
A为n阶正交矩阵的充要条件是:A的列向量组为\(\R^n\)的一组标准正交基
定理有:

不满足的运算定律
- 交换律
- \(AB=BA\)一般不成立,成立时称A B可交换
- 提取公因子时要分清是从左侧还是右侧提出\(AB-B=(A-I)B\)
-

- 消去律
- 当 \(AB = 0\) 时, 不能推出 A = 0 或 B = 0.
- 当 \(AB = AC\), 且 \(A \ne 0\) 时, 不能得到 B = C.
- 注意, 当 A 可逆时, 消去律是成⽴的
其他重要公式
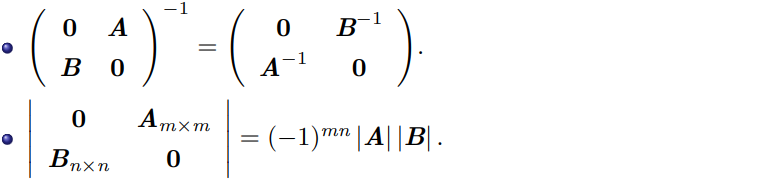
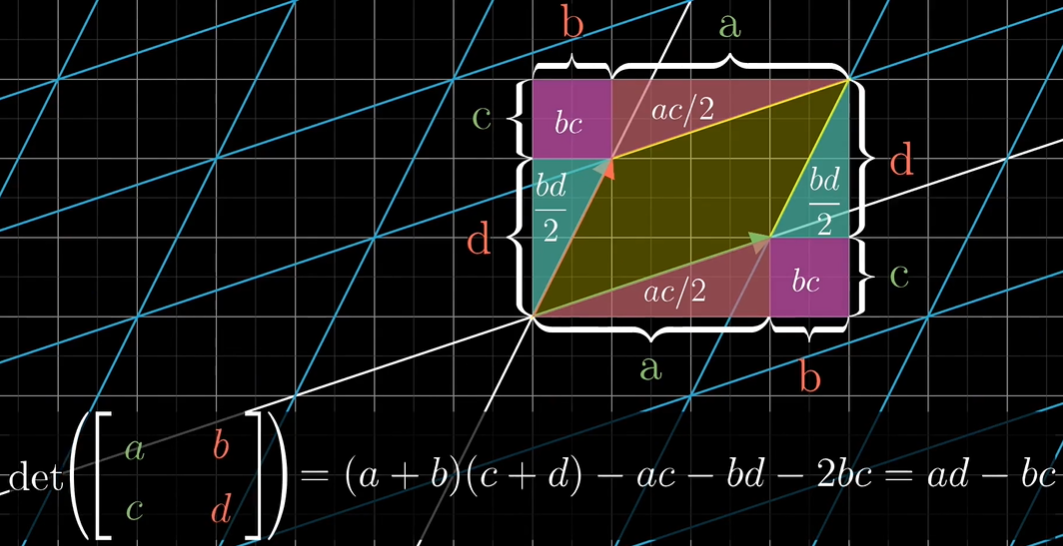
矩阵初等变换

遵循左乘行变,右乘列变的特点
秩 Rank
列空间(Column space)的维数。线是一维,面是二维,列空间就是矩阵的列所张成的空间
秩与列数相等时称为满秩(Full rank)
零向量一定包含在列空间中,因为线性变换零向量的位置不变
变换后落在零向量上的向量构成“零空间”(Null space)或“核”(Kernel)
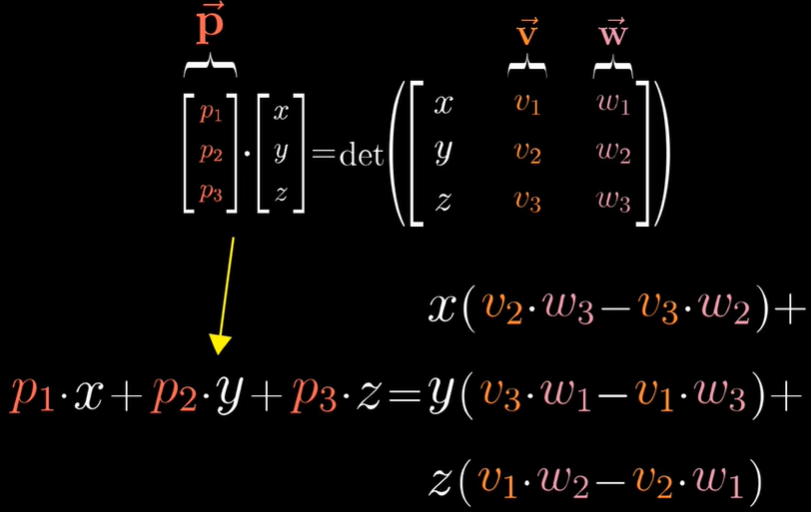
证明\(r(A+B)\le r(A)+r(B)\)
证明\(r(AB)\le min\{r(A),r(B)\}\)
非方阵
例如2*3矩阵,将3维空间的向量映射到2维空间中(本来每个向量使用三维坐标表示的,变成了二维坐标表示)
点积
投影与某个二维向量相关,投影就是将其中一个向量转化为线性变换
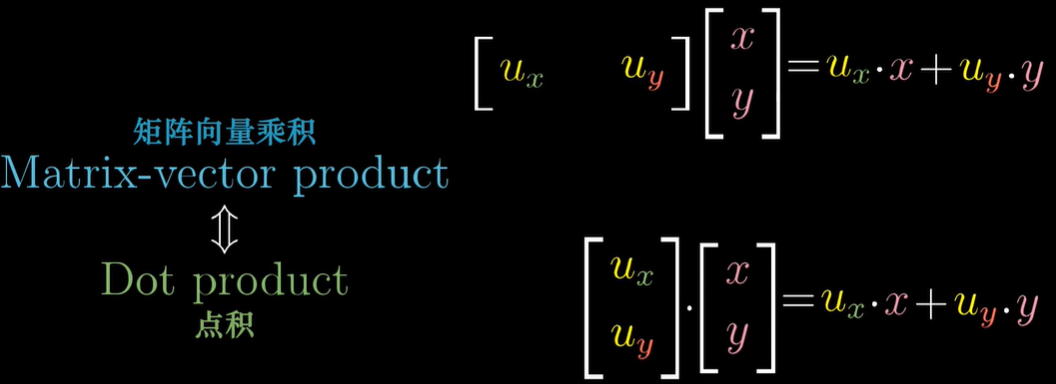
叉积
基向量的顺序就是定向的基础,其值物理意义是构成的平行四边形的面积,即行列式的值. 但叉积的结果是一个与源向量垂直的向量
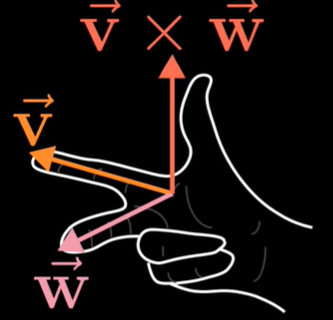
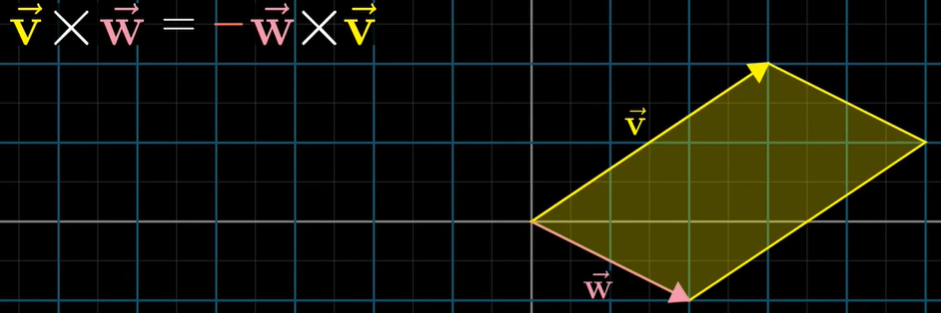
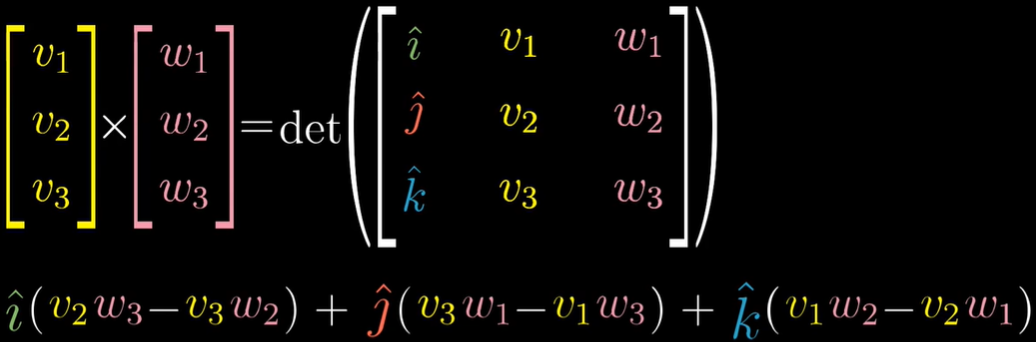
根据点积的几何意义和行列式的几何意义,给定v,w,且(x,y,z)是基向量,可以求得p,即垂直v,w,长度为构成的平行四边形面积。结果意义为平行六面体的体积。

混合积
其意义为a,b,c构成的平行六面体的体积
三个非零向量共面的充要条件是其混合积为0
这三个向量具有轮换对称性
基变换
假设有一个叫jennifer的人使用跟我们不同的基向量(不同的语言),可以用我们的语言来描述她的基向量,得到一个矩阵A(基变换矩阵 change of basis matrix).用她的坐标描述的向量乘该矩阵,得到我们坐标描述的向量(该向量是同一向量,只是基不同),同时可以使用逆矩阵表示相反的过程。


如下形式的公式暗示了一种数学上的转移作用,中间的矩阵表示你所见的变换,而外侧两个矩阵代表转移作用,也就是视角上的转化。矩阵的乘积仍然代表同一个变换,只不过是从其他人的角度来看的
过渡矩阵
过渡矩阵是基与基之间的一个可逆线性变换,在一个空间V下可能存在不同的基。假设有2组基分别为A,B。由基A到基B可以表示为\(B=AP\),过渡矩阵\(P=A^{-1}B\)。它表示的是基与基之间的关系。
设向量在A坐标系下表示为x,在B坐标系下表示为y,有:
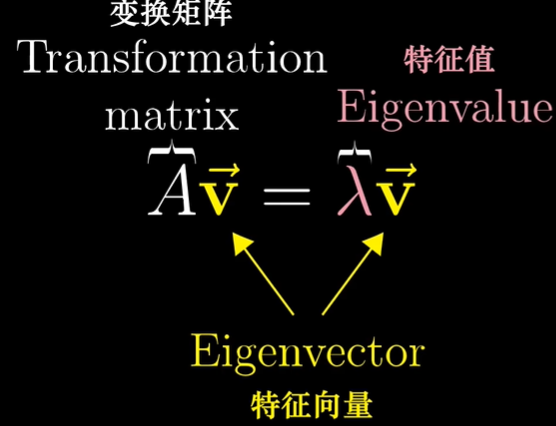
特征值Eigenvalue、特征向量Eigenvector
在线性变换过程中不离开所张成空间的向量称为特征向量,每一个特征向量都有一个特征值,用来衡量特征向量在变换中拉伸或压缩比例的因子。
在3维空间中可以使用特征值为1的特征向量来描述旋转
 $$
(A-\lambda I)\vec{V}=\vec{0}
$$
**当且仅当矩阵代表的变换将空间压缩到更低维度时,才会存时一个非零向量,使得矩阵和它的乘积为零向量,即**$det(A-\lambda I)=0$
$$
(A-\lambda I)\vec{V}=\vec{0}
$$
**当且仅当矩阵代表的变换将空间压缩到更低维度时,才会存时一个非零向量,使得矩阵和它的乘积为零向量,即**$det(A-\lambda I)=0$
不存在实数解时,一般对应于变换中的某种旋转
k重根特征值所对应的线性无关特征向量的个数l,不一定等于特征值的重数k,事实上,l<=k
对角矩阵(Diagonal matrix)的所有基向量都是特征向量,矩阵的对角元是他们所属的特征值
特征基(Eigenbasis),矩阵的特征向量作为基
重要性质
迹
矩阵对角元素之和

运算性质
相似矩阵
存在可逆矩阵P,使得\(P^{-1}AP=B\),称\(A\sim B\) ,AB相似。两者有相同的特征值,但不一定有相同特征向量

正交矩阵

抽象向量空间

相当于程序设计中的接口,定义出一系列的规范,只有符合这个规范就是实现了这个接口,就自动具有了这个接口所拥有的特性。只要满足以上8条公理的东西都可以被称为向量vector。
克莱姆法则Cramer's Rule


克拉默法则⾯对的线性⽅程组要满⾜两个条件:
(1) 未知量个数和⽅程组数相同,
(2) 系数⾏列式 D != 0.
D = 0 是齐次⽅程组有⾮零解的充要条件.
方程组解的判别
非齐次线性方程组Ax=b

- 若\(r(B)=r(A)+1\),则说明方程出现了矛盾,导致方程组无解(消元后B非零行多与A非零行)
- 若\(r(B)=r(A)\),则方程没有矛盾,方程有解
- 当\(r(B)=r(A)=n\)时,没有自由变量,方程有唯一解
- 当\(r(B)=r(A)<n\)时,方程有自由变量,有无穷解
齐次线性方程组Ax=0

对 n 元齐次线性⽅程组 Ax = 0, 设 r(A) = r, 则⽅程组 Ax = 0 的基础解系包含 n − r 个向量
极大无关组
极⼤⽆关组和原向量组是等价的, 是原向量组的简约, 更是原向量组的 “全权代表”
矩阵等价与向量组等价
- 向量组等价, 可得矩阵等价; (注意这里所设的两向量组中向量的个数相 同, 否则两矩阵的列数不同, 会导致矩阵不是同型矩阵, 就不能得到矩阵等价.)
- 矩阵等价, 不能得到向量组等价.
二次型
一个二次齐次多项式一般地可以用矩阵表示为
只含平方项的二次型,称为二次型的标准形
如果标准形的系数只在1,-1,0三个数中取值,称为二次型的规范形
合同矩阵

等价、相似、合同、正交相似
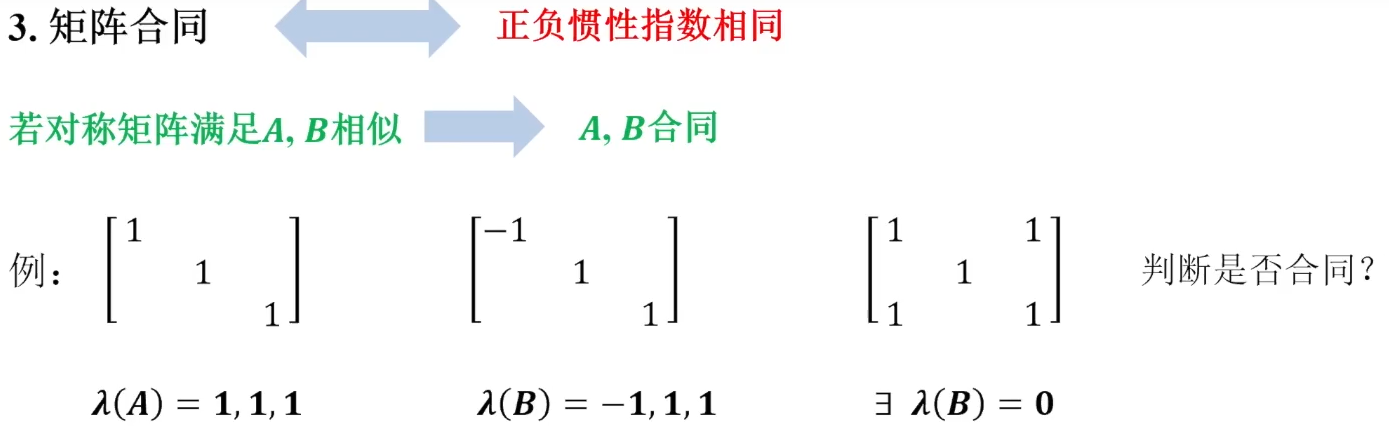
- 正交相似:若A,B均为n阶方阵,存在正交矩阵P,使得\(P^TAP=P^{-1}AP=B\)
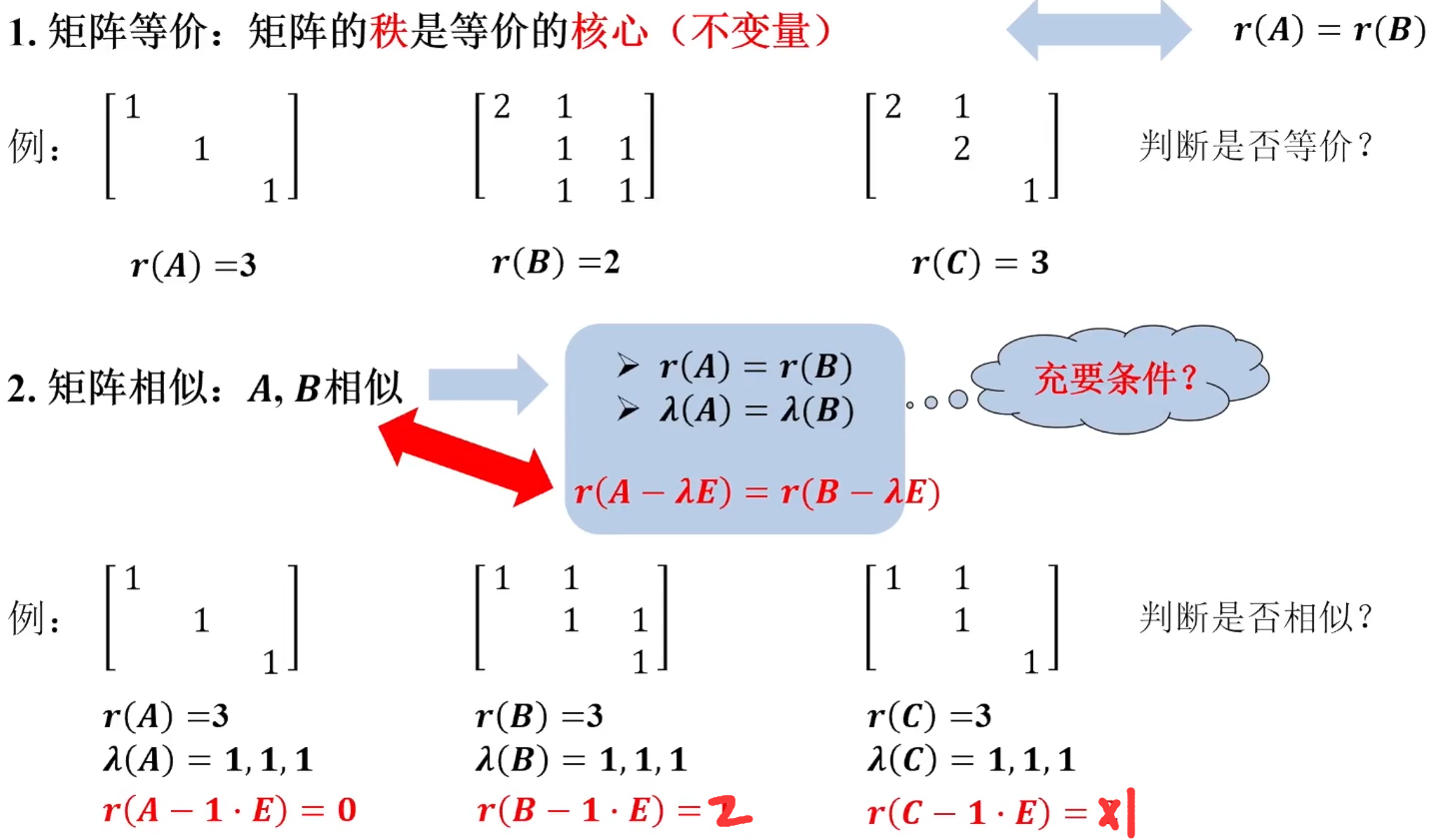
三者之间关系判定


可对角化矩阵
如果一个方块矩阵 A 相似于对角矩阵,也就是说,如果存在一个可逆矩阵 P 使得 \(P^ {−1}AP\) 是对角矩阵,则它就被称为可对角化的。
可对角化的充要条件:n阶矩阵A有n个线性无关的特征向量
注意的问题




 浙公网安备 33010602011771号
浙公网安备 33010602011771号