新生训练选拔模拟-热身赛001题解
前言
应该没有很多人被搞自闭吧,而是应该愈挫愈勇的吧!算法是计算机科学领域最重要的基石之一,很多人都觉得学习最新的语言、技术、标准就是最好的铺路方法,而真正重要的是学习计算机算法和理论,因为计算机语言和开发平台日新月异,但万变不离其宗的是那些算法和理论,例如数据结构、算法、编译原理、计算机体系结构、关系型数据库原理等等 。我们可以把这些基础课程比拟为“内功”,把新的语言、技术、标准比拟为“外功”。 整天赶时髦的人最后只懂得招式,没有功力,是不可能成为高手的。 尤其是算法,它是有灵魂有魅力的,我希望你们都能感受到算法的奇妙美好,虽然可能会碰到 w r o n g a n s w e r wrong\space answer wrong answer,但只要不放弃,总结错误,认真思考,付出行动,总会 A C AC AC的,跟人生一样!
**重点:**一定要补题,可以尝试一下写== B l o g Blog Blog==,这是一个非常不错的习惯,对你的帮助很大。
A.A==B?
-
解题思路
碰到这种没有给出数据范围的题,只是表明是数字,那就要注意是不是大数了。处理大数的方法就是消除前导 0 0 0,这题有点特殊,因为可能是小数,那么如果是有小数部分,那么我们去除前导 0 0 0的时候需要保留小数点前一位的 0 0 0,同时在小数点后的末尾 0 0 0我们同样也要去除,这里如果去除之后所处位是小数点,那么也要将小数点去除。 处理好这样之后,就可以进行比较了。
-
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5;
char a[maxn],b[maxn];
void work(char *s,int &l,int &r){
//去除首0.注意不要清除到小数点。
while(s[l]=='0'&&l<r&&s[l+1]!='.')l++;
//检查是否有小数点。
bool flag=false;
for(int i=l;i<=r;i++){
if(s[i]=='.'){
flag=true;
break;
}
}
//如果有小数点就去除尾0.
if(flag){
while(s[r]=='0')r--;
}
if(s[r]=='.')r--;
}
void solve(){
//去除首0,和小数点之后的0.
int la=0,ra=strlen(a)-1,lb=0,rb=strlen(b)-1;
work(a,la,ra);
work(b,lb,rb);
if(ra-la!=rb-lb){
cout<<"NO"<<endl;
return;
}
else{
//如果长度相同
while(la<=ra){
if(a[la]!=b[lb]){
cout<<"NO"<<endl;
return;
}
la++,lb++;
}
cout<<"YES"<<endl;
}
}
int main(){
while(cin>>a>>b){
solve();
}
return 0;
}
B.The sum problem
-
解题思路
题目中给定的是一个公差为1的等差数列,我们可以直接利用等差数列求和公式来判断,即$m==na_1+\frac{n(n-1)}{2} 。 所 以 我 们 只 要 枚 举 。所以我们只要枚举 。所以我们只要枚举n 就 可 以 得 到 就可以得到 就可以得到a_1 , 然 后 反 过 来 判 断 式 子 是 否 成 立 。 那 么 枚 举 ,然后反过来判断式子是否成立。那么枚举 ,然后反过来判断式子是否成立。那么枚举n 我 们 需 要 确 定 其 上 界 , 为 我们需要确定其上界,为 我们需要确定其上界,为min(sqrt(2m),n) , 因 为 总 共 只 有 ,因为总共只有 ,因为总共只有n 个 , 然 后 结 合 等 差 数 列 公 式 可 得 个,然后结合等差数列公式可得 个,然后结合等差数列公式可得n$的上界。
-
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m;
void solve(){
//题目中给定的是一个公差为1的等差数列,我们可以直接利用求和公式来判断。
//即na1+n*(n-1)/2=m。
//所以我们只要枚举n就可以得到a1,然后反过来判断式子是否成立。
//这时候就可以由求和公式确定n的上界:为sqrt(2*m);
ll temp=min(ll(sqrt(2*m)),n),a1;
for(ll len=temp;len>=1;len--){
a1=(2*m-(len)*(len-1))/(2*len);
if(len*a1+(len)*(len-1)/2==m){
cout<<"["<<a1<<","<<a1+len-1<<"]"<<endl;
}
}
cout<<endl;
}
int main(){
while(cin>>n>>m&&(n||m)){
solve();
}
return 0;
}
C.Drying
-
解题思路、
这题超有意思的啦。我们需要注意到 a i a_i ai的范围,如果我们直接从 1 1 1开始枚举最短时间那是行不通的。诶,刚好昨天下午的帅气学长讲了高效的二分,这里就可以派上用场了,基本思路如下:
l 下界,r 上界 while l<r mid=(l+r)>>1 if(mid 满足我们指定的条件) r=mid else l=mid+1 最后的l就是最优解。那么我们首先需要确定最短时间的上下界,上界肯定是其中衣服水分的最大值,因为最差的时候就是自然风干,下界就设为 0 0 0。最关键的一步就是判断枚举的时间是否成立了,为了提高效率,我们需要对数组进行排序。试想,如果一件衣服能在枚举时间内自然风干,我们可以不使用烘干机。而如果不能,那么我们就需要使用烘干机了,最少使用多少次呢?这里就颇有数学味道了。假设该衣服用来 x x x分钟风干,用了 y y y分钟烘干机。那么可得如下: x + y = t i m e , a i < = x + y × k x+y=time,a_i<=x+y\times k x+y=time,ai<=x+y×k。联立可得 y > = ( a i − t i m e ) / ( k − 1 ) y>=(a_i-time)/(k-1) y>=(ai−time)/(k−1), 这里要取最小上界,所以我们可以加上 k − 2 k-2 k−2.这是常用技巧。加上分母 − 1 -1 −1可以取上界。我们统计所需使用烘干机的时间。将该时间与枚举时间做比较得到我们的结果。
注意,这道题很坑,需要使用
scanf读入数据,或者关闭同步,解除与stdio的绑定,同时用tie函数加速,这样cin,cout就跟scanf差不多了。优化如下:std::ios::sync_with_stdio(false); std::cin.tie(0); std::cout.tie(0); //如果编译开启了 C++11 或更高版本,建议使用 std::cin.tie(nullptr);想了解输入输出优化的可以看这篇:博客链接。
-
代码
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int maxn=1e5+5;
//我们需要求的是时间,而时间恰好是有序的,所以我们可以二分枚举时间。
int n,k;
int a[maxn];
bool check(int time){
//判断所枚举的时间是否可行。
int ans=0;//统计实际用时。
for(int i=n-1;i>=0;i--){
if(a[i]<=time){
//如果当前最大值水分小于等于自然时间,说明剩下的都可以直接风干。
break;
}
else{
ans+=(a[i]-time+k-2)/(k-1);
if(ans>time){
return false;
}
}
}
return true;
}
void solve(){
sort(a,a+n);
if(k==1){
//我们还不如自然风干,自然是最大的水分。
printf("%d\n",a[n-1]);
return;
}
//二分枚举所需时间。
int l=0,r=a[n-1],mid;//最差情况就是衣服水分的最大值,因为这样自然晾干都可以满足。
while(l<r){
mid=(l+r)>>1;
if(check(mid)){
r=mid;
}
else{
l=mid+1;
}
}
printf("%d\n",l);
}
int main(){
while(scanf("%d",&n)!=EOF){
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
}
scanf("%d",&k);
solve();
}
return 0;
}
D.小小粉丝度度熊
-
解题思路
这道题可能偏难一点,由于区间可能会交叉,所以我们需要将这些区间进行处理,变成独立不交叉的区间,即区间合并。我们需要先将区间排序,排序规则为先按左端点位置升序排列再按右端点位置升序排列。之后我们进行如下处理:
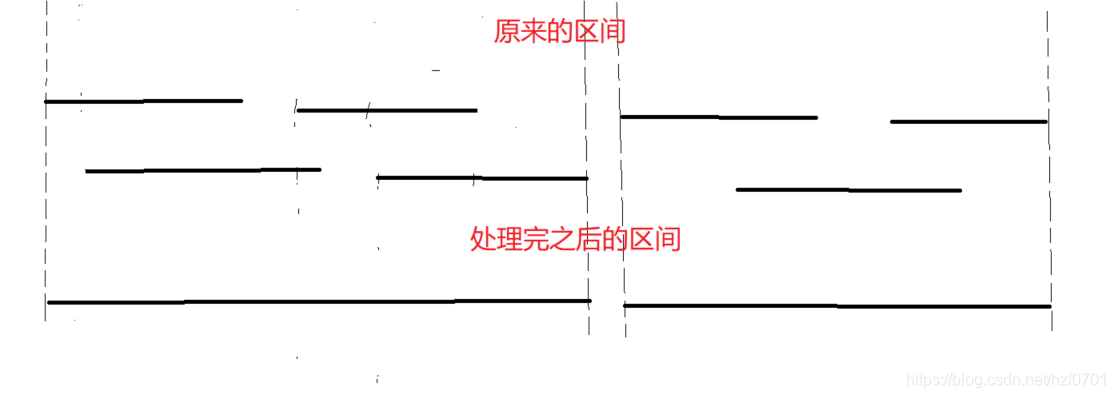
怎么实现呢?我们发现起点左端点是没有变的,而右端点一直在更改,且更改的条件就是下一段区间的左端点在我们更新完的区间内。这样,我们就可以实现了。处理完之后,就是利用尺取法求解最大连续区间,我们利用补签数将这些区间的间隙弥补即可。要注意的就是充分利用尺取法的性质,当两端移动的时候,要对剩余补签数作更新,具体看代码,已贴详细注释。
- 代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
struct Interval{
ll l,r;
bool operator<(const Interval A){
if(l!=A.l)return l<A.l;
else return r<A.r;
}
};
Interval intervals[maxn];
ll n,m;//n个区间m张补签卡。
void solve(){
sort(intervals,intervals+n);
//先将区间处理成不相交的子区间
int i=0,temp,index=0;
ll last;//当前所更新区间的最右端点位置。
while(i<n){
temp=i+1,last=intervals[i].r;
//利用当前区间去更新后面区间。判断条件为左端点是否在该区间内。
while(temp<n&&intervals[temp].l<=last){
//将区间合并,更新该区间的右端点。
last=max(last,intervals[temp].r);
temp++;//继续寻找
}
intervals[index].l=intervals[i].l,intervals[index].r=last;
index++;//新区间数++。
i=temp;//此时temp是不满足条件的,所以我们以此为准去更新区间。
}
//现在我们得到的区间都是有序的,且不相交,所以我们可以利用尺取法来解决。
n=index;//更新区间数量。
/* for(int i=0;i<n;i++){
printf("[%d,%d]\n",intervals[i].l,intervals[i].r);
} */
ll ans=m;//ans代表签到数,由于有m张补签卡,至少会签到m次。
temp=m;//temp代表的是补签数量
int l=0,r=0;
while(r<n){
//尺取法
while(r+1<n&&intervals[r+1].l-intervals[r].r-1<=temp){
//固定左端点,右端点不断移动。
temp-=intervals[r+1].l-intervals[r].r-1;//补签,使得变为连续区间。
r++;
}
ans=max(ans,intervals[r].r-intervals[l].l+temp+1);
//移动l,处理清楚补签次数。
if(l+1<n&&intervals[l+1].l-intervals[l].r-1>0&&intervals[l+1].l-intervals[l].r-1+temp<=m){
//如果该区间空隙被补过,就清除影响,因为我们要做下次移动了。
temp+=intervals[l+1].l-intervals[l].r-1;
}
l++;
while(l>r)r++;//确保r大于等于l。
}
cout<<ans<<endl;
}
int main(){
while(cin>>n>>m){
for(int i=0;i<n;i++){
cin>>intervals[i].l>>intervals[i].r;
}
solve();
}
return 0;
}
E.今年暑假不AC
-
解题思路
纯粹的贪心题。我们的贪婪目标就是看的节目越多越好,所以我们只在意节目什么时候结束且能完整的看完这个节目即可。那么我们对这些节目按结束时间由小到大排序。然后遍历所有节目统计即可。注意这里为什么是结束时间最早而不是起始时间最早或者结束时间最早呢?因为只有结束时间才能决定我们看更多的节目。
-
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=105;
int n;
struct node{
int st,ed;
//贪心,将节目排满即可。
bool operator<(const node a){
return ed<a.ed;//我们只关心什么时候结束,越早结束越好。
}
};
node times[maxn];
void solve(){
sort(times,times+n);
int ans=0,ed=0;
for(int i=0;i<n;i++){
if(times[i].st>=ed){
ans++;
ed=times[i].ed;
}
}
cout<<ans<<endl;
}
int main(){
while(cin>>n&&n){
for(int i=0;i<n;i++){
cin>>times[i].st>>times[i].ed;
}
solve();
}
return 0;
}
F.一卡通大冒险
-
解题思路
将这道题视为动态规划处理的话,我们需要定义一个状态,即 d p [ i ] [ j ] dp[i][j] dp[i][j],我们设这表示的就是 i i i个人分成 j j j个非空集合的方案数,那么这个状态是由什么得来的呢?即 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]和 d p [ i − 1 ] [ j ] ∗ j dp[i-1][j]*j dp[i−1][j]∗j,这 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]变成 d p [ i ] [ j ] dp[i][j] dp[i][j]代表的意思就是当第 i i i个人不加入现有的 j − 1 j-1 j−1个集合中,而自己创建一个集合,那么方案数自然是不变的。 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]变成 d p [ i ] [ j ] dp[i][j] dp[i][j]代表的意思就是当第 i i i个人加入现有的 j j j个集合中,那么其有 j j j中选择方案,故 × j \times j ×j。得到所有状态之后我们就可以统计了,即 r e s u l t [ i ] = ∑ j = 1 i d p [ i ] result[i]=\sum _{j=1}^{i}dp[i] result[i]=∑j=1idp[i]。
那这道题其实还可以看做一道组合数学推导题,就相当于将 n n n个有区别的球放到 m m m个相同的盒子中,要求无一空盒,这种方案数我们用 S n m S_n^m Snm来表示,这个被称为第二类 s t r i l i n g striling striling数。那么公式即为:
S ( n , m ) = S ( n − 1 , m − 1 ) + m S ( n − 1 , m ) , S ( n , 1 ) = S ( n , n ) = 1 。 S(n,m)=S(n-1,m-1)+mS(n-1,m),S(n,1)=S(n,n)=1。 S(n,m)=S(n−1,m−1)+mS(n−1,m),S(n,1)=S(n,n)=1。
-
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e3+2;
const int mod=1e3;
int t,n;
int dp[maxn][maxn];//dp[i][j]表示i个人分j个集合的方法
int result[maxn];
void init(){
dp[1][1]=1;//初始状态,当只有1个人的时候只能分一个集合。
result[1]=1;
for(int i=2;i<=2000;i++){
dp[i][1]=1,dp[i][i]=1;
result[i]=2;//至少存在以上两种情况。
for(int j=2;j<i;j++){
dp[i][j]=dp[i-1][j-1]+dp[i-1][j]*j;
dp[i][j]%=1000;
result[i]+=dp[i][j];
}
result[i]%=1000;
}
}
void solve(){
}
int main(){
init();
while(cin>>t){
while(t--){
cin>>n;
cout<<result[n]<<endl;
}
}
return 0;
}
总结
呃呃呃,我不是故意的,这题我也没看过,只知道它们的类型,不过其实也还好,恰好刚讲完二分和双指针嘛,现学现用,不要觉得很难,把不懂的搞懂,那么以后碰到就会了。希望大家能够抓紧时间,好好准备接下来的选拔赛。
}
result[i]%=1000;
}
}
void solve(){
}
int main(){
init();
while(cin>>t){
while(t–){
cin>>n;
cout<<result[n]<<endl;
}
}
return 0;
}
# 总结
~~==呃呃呃,我不是故意的,这题我也没看过,只知道它们的类型,不过其实也还好,恰好刚讲完二分和双指针嘛,现学现用==~~,不要觉得很难,把不懂的搞懂,那么以后碰到就会了。希望大家能够抓紧时间,好好准备接下来的选拔赛。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号