P4147 玉蟾宫 题解

给定一个 \(n \times m\) 的矩阵，找出最大矩形，满足所有元素为 F，输出这个矩形的大小 \(\times 3\)。

悬线法。

用 \(h\) 记录悬线长度，每个矩形的高一定是一个悬线。接下来用 \(l\) 和 \(r\) 记录悬线左右最远能到的位置，求 \(h,l,r\) 方法如下：

• \(h\) 数组：初始化为 \(1\)。对于所有的 \((i,j) \mid i>1\)，如果 \(a_{i,j}=\tt F\) 且 \(a_{i-1,j}=\tt F\)，那么 \(h_{i,j}=h_{i-1,j}+1\)。
• \(l\) 数组：初始化为当前列。如果 \(a_{i,j}=\tt F\)，且 \(a_{i,j-1}=\tt F\)，那么 \(l\) 可以往左扩展，\(l_{i,j}=l_{i,j-1}\)。
• \(r\) 数组：初始化为当前列。采用倒序循环，如果 \(a_{i,j}=\tt F\)，且 \(a_{i,j-1}=\tt F\)，那么 \(r\) 可以往右拓展，\(r_{i,j}=r_{i+1,j}\)。

其中 \(l\) 和 \(r\) 记录的是悬线左右最远能到的位置，那么我们就要处理这种情况：

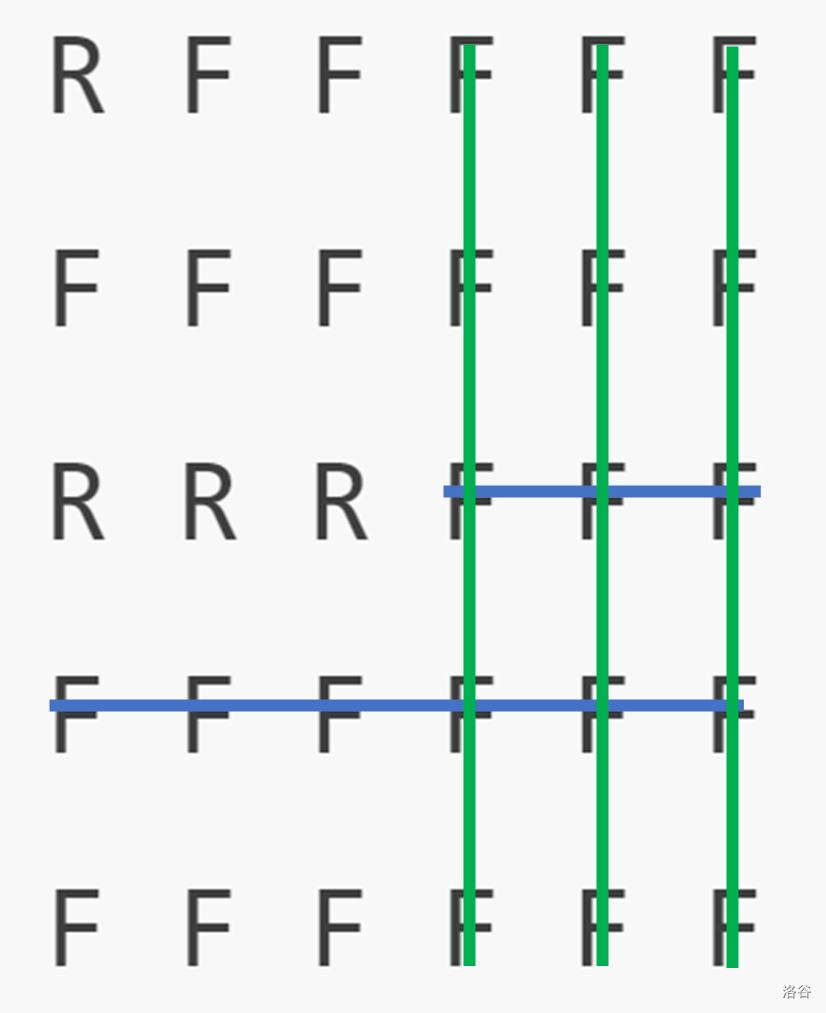
其中按照如上方式更新 \(l,r\)，那么第四列里都是 \(l=1,r=6\)，无法正确计算右边的悬线为高时的矩形的面积，因此我们需要再更新一次 \(l\) 和 \(r\) 数组。当存在悬线时，悬线上的 \(l,r\) 保持相同，应均为原来的最小值。

#include <bits/stdc++.h>

#define int long long

using namespace std;

int n, m;
char a[1005][1005];
int l[1005][1005], r[1005][1005], h[1005][1005];
int ans;

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    cin >> n >> m;
    
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
            // 初始化
            h[i][j] = 1;
            l[i][j] = j, r[i][j] = j;
        }
    }
    
    for (int i = 1; i <= n; i++) {
        // 求 l 和 r
        for (int j = 2; j <= m; j++) {
            if (a[i][j] == 'F' && a[i][j - 1] == 'F') {
                l[i][j] = l[i][j - 1];
            }
        }
        for (int j = m - 1; j >= 1; j--) {
            if (a[i][j] == 'F' && a[i][j + 1] == 'F') {
                r[i][j] = r[i][j + 1];
            }
        }
        // 更新 l 和 r
        if (i > 1) {
            for (int j = 1; j <= m; j++) {
                if (a[i][j] == 'F' && a[i - 1][j] == 'F') {
                    if (l[i - 1][j] > l[i][j]) {
                        l[i][j] = l[i - 1][j];
                    }
                    if (r[i - 1][j] < r[i][j]) {
                        r[i][j] = r[i - 1][j];
                    }
                }
            }
        }
    }
    
    // 求 h
    for (int i = 2; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (a[i][j] == 'F' && a[i - 1][j] == 'F') {
                h[i][j] = h[i - 1][j] + 1;
            }
        }
    }

    // 统计答案，枚举所有悬线为高时的情况
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (a[i][j] == 'F') {
                ans = max(ans, (r[i][j] - l[i][j] + 1) * h[i][j]);
            }
        }
    }
    
    cout << ans * 3 << "\n";
    
    return 0;
}