Solution P11025 [COTS 2020] 辣椒 Sadnice

首先由于最后的结果是生成树，因此连通块数即为切断的边数加一。

考虑假设有 \(a\) 条竖边，\(b\) 条横边，有 \(a+b=(n+1)(m+1)-1=nm+n+m\)。由于破坏者会每次选择切掉更多的边，分别对于横边和竖边均匀分配（先假设这是可以被构造到的），此时切断边数为 \(\max\left(\left\lceil\frac an\right\rceil,\left\lceil\frac bm\right\rceil\right)\)。

枚举后假设我们找到了最优的一组 \(a,b\)，考虑如下图方式调整：

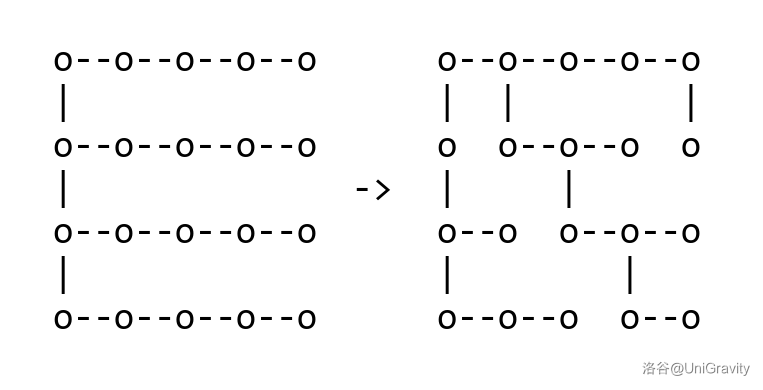
我们知道连接两列之间横向边需要被删掉几条，只需轮流选择哪一行的将其重新向上定向即可。不难发现此时图仍然连通。

const int N=1005;
int n,m,a,b;
bool dw[N][N],rt[N][N];

signed main(){
    n=read(),m=read();
    int res=0x3f3f3f3f;
    forto(i,1,(n+1)*(m+1)){
        int a1=i,b1=n*m+n+m-a1;
        if(a1<n||b1<m)continue;
        int v=max((a1-1)/n,(b1-1)/m)+1;
        if(v<res)res=v,a=a1,b=b1;
    }
    cerr<<a<<' '<<b<<' '<<res<<'\n';     
    a=((a-1)/n+1)*n,b=((b-1)/m+1)*m;
    cerr<<a/n<<' '<<b/m<<'\n';
    forto(i,1,n)dw[i][1]=1;
    forto(i,1,n+1)forto(j,1,m)rt[i][j]=1;
    int id=1;
    forto(j,2,m+1){
        int cnt=n+1-b/m;
        while(cnt--){
            dw[id][j]=1,rt[id+1][j-1]=0;
            id++;if(id>n)id=1;
        }
    }
    forto(i,1,n+1){
        forto(j,1,m+1){
            printf("o");
            if(j>m)continue;
            printf(rt[i][j]?"--":"  ");
        }
        printf("\n");
        if(i>n)continue;
        forto(j,1,m+1){
            printf(dw[i][j]?"|":" ");
            if(j>m)continue;
            printf("  ");
        }
        printf("\n");
    }
    return 0;
}