一类与子集和相关的构造问题

CF618F Double Knapsack

给你两个元素个数均为 \(n\) 的可重集 \(A,B\)，每个元素的大小在 \([1,n]\) 内。分别找出 \(A,B\) 的子集，使得它们中的元素之和相等。\(n\le10^6\)。

先转化问题，将 \(B\) 中的元素取反后加入 \(A\)，就变成找出 \(A\) 的一个子集和为 \(0\)。

发现子集很多而值比较小，可以猜想应该不难找到答案。但是由于子集的限制太宽且不好刻画，因此考虑转成选择 \(A\) 的一个子串和为 \(0\)。这个子串的顺序由我们确定。

这里可以考虑鸽巢原理，考虑子串的每个前缀之和共 \(2n+1\) 个（空前缀也算），则我们只需让所有前缀只有最多 \(2n\) 个取值即可。

考虑初始前缀和 \(s=0\)，接下来分类讨论：

• 如果 \(s\le0\)，则选择一个 \(A\) 中数加上去。由于数的范围为 \([1,n]\)，因此 \(s\) 的上界为 \(n\)。
• 如果 \(s>0\)，则选择 \(B\) 中一个数（为负数）加上去，\(s\) 下界为 \(-n+1\)。

发现 \(s\) 的范围为 \([-n+1,n]\)。

但我们发现可能出现 \(A\) 中数选完而 \(B\) 还没选完的情况，此时 \(s\) 可能超出范围。但如果选数时 \(A\) 已经选完了，我们发现每次选 \(A\) 时都有 \(s\le 0\)，而由于 \(s>-n\)，因此 \(x\) 有 \(n\) 个取值。而加上这次 \(A\) 取完了而仍然 \(s\le 0\)，一共有 \(n+1\) 次出现 \(s\le 0\) 的情况，因此一定存在重复。

同理对于 \(B\) 选完，\(s>0\) 共 \(n\) 个取值，而有 \(n+1\) 次会出现 \(s>0\)，一定存在重复。

扫一遍用栈记录即可做到线性。

---

发现这类问题的套路为：先将子集和转化为子串和的形式，然后使用鸽巢原理等解决。

CF1270G Subset with Zero Sum

给你 \(n\) 个整数 \(a_1,a_2,\dots,a_n\)，满足 \(a_i\in[i-n,i-1]\)。
找到一个这些整数的一个非空子集，使得它们的和为 \(0\)。

考虑还是确定顺序后利用鸽巢原理。一共有 \(n+1\) 个前缀和，需要找到一种顺序使得前缀和的值域大小小于等于 \(n\)。

这种问题可以画折线图。考虑当前的前缀和为 \(s\)，我们要让前缀和在 \([0,n)\) 内。

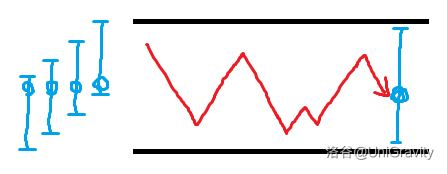
发现每个不同的 \(s\in[0,n)\) 都有唯一一个确定的 \(i\) 满足 \(s\) 加上 \(a_i\) 后值一定还在 \([0,n)\) 内。

那么每次找出 \(s\) 对应的 \(i\) 加入序列末尾即可，直到这个 \(s\) 出现过。由于出现之前的 \(s\) 两两不同，因此对应的 \(i\) 也两两不同。

---

这个思路也可以应用在背包 dp 优化内。

经典题

有 \(n\) 个体积为 \(a_i\) 的物品，你有一个容量为 \(m\) 的背包，要求选一些数使得背包中物品的体积最大（即物品没有价值，要求背包空的部分尽量小）。\(1\le n,a_i\le 10^3,1\le m\le\sum_{i=1}^na_i\)。

直接暴力背包，时间复杂度是 \(O(n^2V)\) 的（\(V=\max a_i\)）。

发现主要问题在于 \(m\) 是 \(nV\) 级别的，考虑如何缩小 \(m\)。

我们可以先贪心找出一组解，即如果背包能塞下就尽量塞。判掉 \(m>\sum a_i\) 的情况，那么此时使用的容量 \(s\) 满足 \(s\in(m-V,m]\)。

考虑在这个贪心解的基础上调整，不在解内的权值为正，否则为负（类似于反悔），而背包最大容量为 \(m-s\le V\)，要求选一些数使得在背包被占用空间尽量大。

但是仍然可能出现过程中背包塞了 \(\ge V\) 的体积。考虑采用上文 CF618F 的思路，对正负数分开考虑。

对于一组最后和在 \([0,m-s]\) 范围内的解，将其正负数分别拿出来考虑。正数和负数内部的选择顺序是固定的，而二者直接的顺序任意（类似与做归并排序）。那么发现假如当前前缀和大于等于 \(V\) 就加负数，否则加正数，此时过程中的前缀和均小于等于 \(2V\)。那么值域就只要开 \(O(V)\) 大小了。

设计状态：\(f_{i,j,k}\) 表示是否能满足选了前 \(i\) 个正数，前 \(j\) 个负数，选出数和为 \(k\ (0\le k\le 2V)\)。这是一个可行性的状态，可以利用单调性优化。即由于在 \(i,k\) 确定的情况下 \(j\) 越小则越有可能，因此设 \(g_{i,k}\) 表示选了前 \(i\) 个数，和为 \(k\) 时最小的 \(j\) 即可。时间复杂度 \(O(nV)\)。