光程最短原理

一、折射定律-费马最短路推导

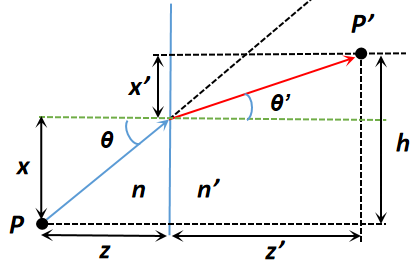
计算整个折射路径的长度，分为两段：第一段为原始介质中光束所走过的路程，第二段为光束在折射介质中走过的路程：

\[L = n\times \sqrt{z^2+ x^2} + n'\times \sqrt{z'^2+x'^2} \]

要使得光程最短，实际就是 \(x'\) 的位置需要调整改变：

\[\begin{split} f(x) &= n \sqrt{z^2+ x^2} + n' \sqrt{z'^2+x'^2} \\ &=n \sqrt{z^2+ x^2} + n' \sqrt{z'^2+(h-x)^2} \end{split} \]

求解上述公式关于 \(x\) 倒数为零的点，即为所需要的最短路径点：

\[\begin{split} f'(x) &= n*\frac{x}{\sqrt{z^2+ x^2}} - n'* \frac{(h-x)}{\sqrt{z'^2+(h-x)^2}}= 0 \\ &=> nsin\theta - n'sin\theta' = 0 \\ &=> \frac{n}{n'} = \frac{sin \theta}{sin \theta'} \end{split} \]

推导手稿

二、反射定律-费马最短路推导

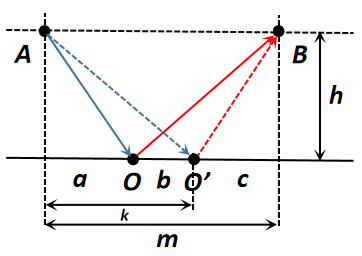
考虑 \(L = |AO|+|OB|=|AO'|+|O'B| \tag{2.1} ; \ b \rightarrow 0\) 光程相等时的位置点 \(O\) 即为极值点位置(实际上就是在 \(O\) 点的导数为 0 ，无变化)，此时的极值点即为反射点：

\[\begin{align} |AO'|=\sqrt{(a+b)^2+ h^2} \tag{2.2}\\ |AO|=\sqrt{(a)^2+ h^2} \tag{2.3}\\ |OB'|=\sqrt{(c)^2+ h^2} \tag{2.4}\\ |OB|=\sqrt{(b+c)^2+ h^2} \tag{2.5}\\ \end{align} \]

将上述公式代入到式 \(2.1\) 中可得：

\[\begin{split} L &= \sqrt{(a+b)^2+ h^2} + \sqrt{(c)^2+ h^2} = \sqrt{(a)^2+ h^2} + \sqrt{(b+c)^2+ h^2}, \ b \rightarrow 0 \\ &= \sqrt{k^2+ h^2} + \sqrt{(c)^2+ h^2} \ \text{取到最小值, k 与 c 的关系}\\ &\Rightarrow f(c)= \sqrt{(m-c)^2+ h^2} + \sqrt{c^2+ h^2} \\ &\Rightarrow f'(c)=\frac{c-m}{\sqrt{(m-c)^2+ h^2}} + \frac{c}{\sqrt{c^2+ h^2}} \end{split} \]

考虑上述 \(f'(c)\) 导数为 0 的位置，则有：

\[\begin{split} f'(c) &=\frac{c-m}{\sqrt{(m-c)^2+ h^2}} + \frac{c}{\sqrt{c^2+ h^2}} = 0\\ &\Rightarrow \frac{m-c}{\sqrt{(m-c)^2+ h^2}} = \frac{c}{\sqrt{c^2+ h^2}} \ \text{两边同时平方化简}\\ &\Rightarrow m=2c \end{split} \]

\(c=\frac{m}{2}\) 即为反射点位置

推导手稿

Reference

1. 用几何法证明光的折射定律