代码随想录算法训练营第二十一天 | 235. 二叉搜索树的最近公共祖先，701.二叉搜索树中的插入操作，450.删除二叉搜索树中的节点

一、参考资料

二叉搜索树的最近公共祖先

题目链接/文章讲解：https://programmercarl.com/0235.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E7%9A%84%E6%9C%80%E8%BF%91%E5%85%AC%E5%85%B1%E7%A5%96%E5%85%88.html

视频讲解：https://www.bilibili.com/video/BV1Zt4y1F7ww

二叉搜索树中的插入操作

题目链接/文章讲解：https://programmercarl.com/0701.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E6%8F%92%E5%85%A5%E6%93%8D%E4%BD%9C.html

视频讲解：https://www.bilibili.com/video/BV1Et4y1c78Y

删除二叉搜索树中的节点

题目链接/文章讲解：https://programmercarl.com/0450.%E5%88%A0%E9%99%A4%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E8%8A%82%E7%82%B9.html

视频讲解：https://www.bilibili.com/video/BV1tP41177us

二、LeetCode235. 二叉搜索树的最近公共祖先

https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/description/

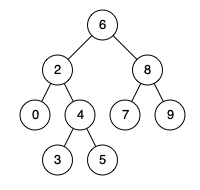
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
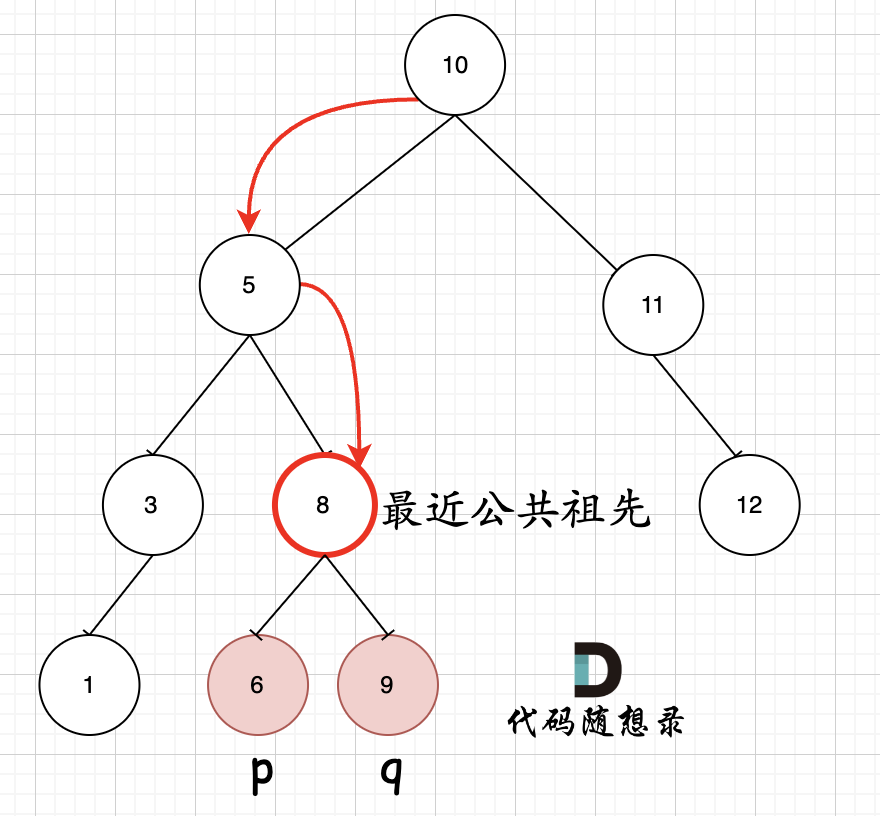
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（ 一个节点也可以是它自己的祖先）。”
例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]【如上图】

示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
 // version1:递归版
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == NULL) return NULL;
        // 左
        if (root->val > p->val && root->val > q->val) {
            TreeNode* left = lowestCommonAncestor(root->left, p, q);
            if (left != NULL) return left;
        }
        // 右
        if (root->val < p->val && root->val < q->val) {
            TreeNode* right = lowestCommonAncestor(root->right, p, q);
            if (right != NULL) return right;
        }
        // 一边大一边小，当前节点在p和q中间，或者等于p，或者等于q
        return root;
    }
};
// version2：递归精简版
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == NULL) return NULL;
        if (root->val > p->val && root->val > q->val) {
            return lowestCommonAncestor(root->left, p, q);
        }
        if (root->val < p->val && root->val < q->val) {
            return lowestCommonAncestor(root->right, p, q);
        }
        return root;
    }
};

迭代法：

 // version3：迭代版
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while (root) {
            if (root->val > p->val && root->val > q->val) {
                root = root->left;
            } else if (root->val < p->val && root->val < q->val) {
                root = root->right;
            } else return root;
        }
        return NULL;
    }
};

三、LeetCode701.二叉搜索树中的插入操作

https://leetcode.cn/problems/insert-into-a-binary-search-tree/description/

示例1：

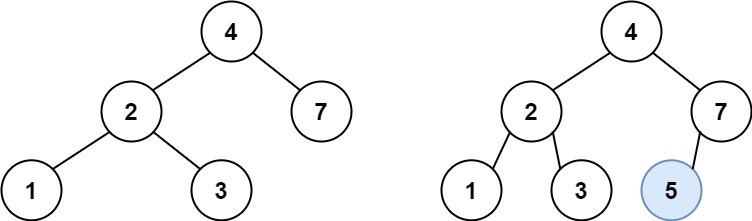
示例一的另一个图

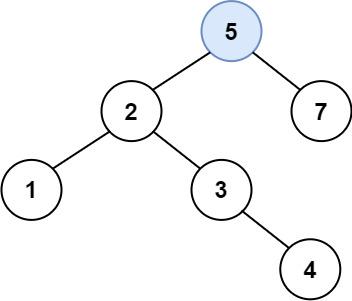
给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。
注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：
输入：root = [4,2,7,1,3], val = 5 输出：[4,2,7,1,3,5] 解释：另一个满足题目要求可以通过的树是： 【如上图】

示例 2：
输入：root = [40,20,60,10,30,50,70], val = 25 输出：[40,20,60,10,30,50,70,null,null,25]
示例 3：
输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 输出：[4,2,7,1,3,5]
提示：
树中的节点数将在 [0, 10^4]的范围内。
-10^8 <= Node.val <= 10^8
所有值 Node.val 是 独一无二 的。
-10^8 <= val <= 10^8
保证 val 在原始BST中不存在。 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 // version1：递归法，每次的节点都插入到叶子节点的位置
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        // 找到了插入的位置
        if (root == NULL) {
            TreeNode* node = new TreeNode(val);
            return node;
        } else if (root->val > val) {
            root->left = insertIntoBST(root->left, val);
        } else {
            root->right = insertIntoBST(root->right, val);
        }
        return root;
    }
};

迭代法：【参考卡哥文章讲解】

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == NULL) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        TreeNode* cur = root;
        TreeNode* parent = root; // 这个很重要，需要记录上一个节点，否则无法赋值新节点
        while (cur != NULL) {
            parent = cur;
            if (cur->val > val) cur = cur->left;
            else cur = cur->right;
        }
        TreeNode* node = new TreeNode(val);
        if (val < parent->val) parent->left = node;// 此时是用parent节点的进行赋值
        else parent->right = node;
        return root;
    }
};

注意本身递归的过程就有优化，迭代的方法就需要记录当前遍历节点的父节点了，这个和没有返回值的递归函数实现的代码逻辑是一样的，而递归是不需要，因为它直接返回了，与刚刚插入的节点正好完成了衔接。

四、LeetCode450.删除二叉搜索树中的节点

https://leetcode.cn/problems/delete-node-in-a-bst/description/

示例一：

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。
一般来说，删除节点可分为两个步骤：
首先找到需要删除的节点；
如果找到了，删除它。

示例 1:

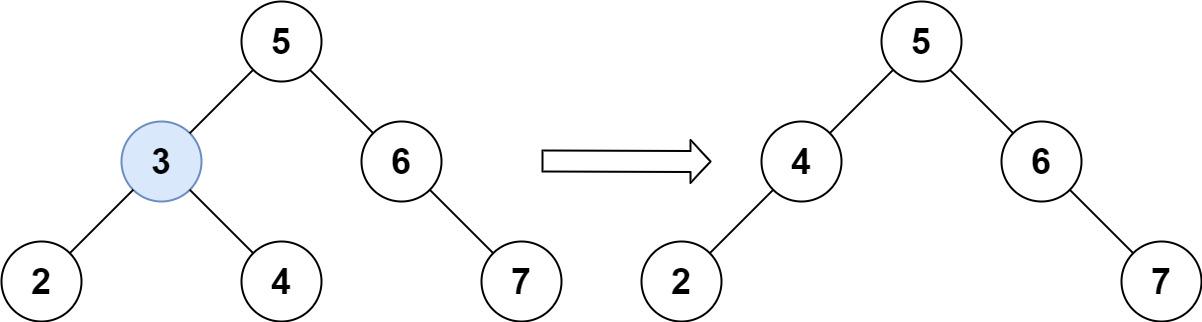
输入：root = [5,3,6,2,4,null,7], key = 3 输出：[5,4,6,2,null,null,7] 解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0 输出: [5,3,6,2,4,null,7] 解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0 输出: []

提示:
节点数的范围 [0, 10^4].
-10^5 <= Node.val <= 10^5
节点值唯一
root 是合法的二叉搜索树
-10^5 <= key <= 10^5

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。 
// 我根据视频讲解思路理解写的代码：
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //看视频听懂了思路，我来写写试试。一共有五种情况（左空右空，左不空右空，左空右不空，左不空右不空）
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == NULL) return NULL;
        if (root->val == key) {
            if (!root->left && !root->right) {
                return NULL;
            } else if (root->left && !root->right) {
                return root->left;
            } else if (!root->left && root->right) {
                return root->right;
            } else {
                TreeNode* cur = root->right;
                while (cur->left) cur = cur->left;
                cur->left = root->left;
                return root->right;
            }
        }
        if (root->val > key) root->left = deleteNode(root->left, key);
        if (root->val < key) root->right = deleteNode(root->right, key);
        return root;
    }
};
// 稍微简化一些
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 //看视频听懂了思路，我来写写试试。一共有五种情况（左空右空，左不空右空，左空右不空，左不空右不空）
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == NULL) return NULL;
        if (root->val == key) {
            if (!root->left && !root->right) return NULL;
            else if (root->left && !root->right) return root->left;
            else if (!root->left && root->right) return root->right;
            else {
                TreeNode* cur = root->right;
                while (cur->left) cur = cur->left;
                cur->left = root->left;
                return root->right;
            }
        }
        if (root->val > key) root->left = deleteNode(root->left, key);
        if (root->val < key) root->right = deleteNode(root->right, key);
 
        return root;
    }
};

卡哥文章详解——五种情况的具体分析：

  • 第一种情况：没找到删除的节点，遍历到空节点直接返回了

  • 找到删除的节点

  • 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点

  • 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点

  • 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点

  • 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

对应注释版本代码

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) return root; // 第一种情况：没找到删除的节点，遍历到空节点直接返回了
        if (root->val == key) {
            // 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
            if (root->left == nullptr && root->right == nullptr) {
                ///! 内存释放
                delete root;
                return nullptr;
            }
            // 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点
            else if (root->left == nullptr) {
                auto retNode = root->right;
                ///! 内存释放
                delete root;
                return retNode;
            }
            // 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
            else if (root->right == nullptr) {
                auto retNode = root->left;
                ///! 内存释放
                delete root;
                return retNode;
            }
            // 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
            // 并返回删除节点右孩子为新的根节点。
            else {
                TreeNode* cur = root->right; // 找右子树最左面的节点
                while(cur->left != nullptr) {
                    cur = cur->left;
                }
                cur->left = root->left; // 把要删除的节点（root）左子树放在cur的左孩子的位置
                TreeNode* tmp = root;   // 把root节点保存一下，下面来删除
                root = root->right;     // 返回旧root的右孩子作为新root
                delete tmp;             // 释放节点内存（这里不写也可以，但C++最好手动释放一下吧）
                return root;
            }
        }
        if (root->val > key) root->left = deleteNode(root->left, key);
        if (root->val < key) root->right = deleteNode(root->right, key);
        return root;
    }
};

迭代法：（这个题的迭代法没有做过多研究）

class Solution {
private:
    // 将目标节点（删除节点）的左子树放到 目标节点的右子树的最左面节点的左孩子位置上
    // 并返回目标节点右孩子为新的根节点
    // 是动画里模拟的过程
    TreeNode* deleteOneNode(TreeNode* target) {
        if (target == nullptr) return target;
        if (target->right == nullptr) return target->left;
        TreeNode* cur = target->right;
        while (cur->left) {
            cur = cur->left;
        }
        cur->left = target->left;
        return target->right;
    }
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) return root;
        TreeNode* cur = root;
        TreeNode* pre = nullptr; // 记录cur的父节点，用来删除cur
        while (cur) {
            if (cur->val == key) break;
            pre = cur;
            if (cur->val > key) cur = cur->left;
            else cur = cur->right;
        }
        if (pre == nullptr) { // 如果搜索树只有头结点
            return deleteOneNode(cur);
        }
        // pre 要知道是删左孩子还是右孩子
        if (pre->left && pre->left->val == key) {
            pre->left = deleteOneNode(cur);
        }
        if (pre->right && pre->right->val == key) {
            pre->right = deleteOneNode(cur);
        }
        return root;
    }
};

普通二叉树的删除方式

通用的删除，普通二叉树的删除方式（没有使用搜索树的特性，遍历整棵树），用交换值的操作来删除目标节点。

代码中目标节点（要删除的节点）被操作了两次：

  • 第一次是和目标节点的右子树最左面节点交换。

  • 第二次直接被NULL覆盖了。

代码如下：

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) return root;
        if (root->val == key) {
            if (root->right == nullptr) { // 这里第二次操作目标值：最终删除的作用
                return root->left;
            }
            TreeNode *cur = root->right;
            while (cur->left) {
                cur = cur->left;
            }
            swap(root->val, cur->val); // 这里第一次操作目标值：交换目标值其右子树最左面节点。
        }
        root->left = deleteNode(root->left, key);
        root->right = deleteNode(root->right, key);
        return root;
    }
};

卡哥总结：

二叉搜索树删除节点比增加节点复杂的多。

因为二叉搜索树添加节点只需要在叶子上添加就可以的，不涉及到结构的调整，而删除节点操作涉及到结构的调整。

这里我们依然使用递归函数的返回值来完成把节点从二叉树中移除的操作。

这里最关键的逻辑就是第五种情况（删除一个左右孩子都不为空的节点），这种情况一定要想清楚。

而且就算想清楚了，对应的代码也未必可以写出来，所以这道题目既考察思维逻辑，也考察代码能力。

递归中我给出了两种写法，推荐大家学会第一种（利用搜索树的特性）就可以了，第二种递归写法其实是比较绕的。【第二种指普通二叉树的删除节点】

总结：

博客补完了！成就感up，继续加油叭~还剩最后一天树的题目，一鼓作气写完，木有休息的休息日哈哈哈，不过是值得的，总算是赶上了进度。

posted @   ZYM-爱吃柚子的程序媛  阅读(364)  评论(0)  编辑  收藏  举报
相关博文：
· 代码随想录算法训练营第二十天 | 530.二叉搜索树的最小绝对差，501.二叉搜索树中的众数，236. 二叉树的最近公共祖先
· 代码随想录算法训练营第二十三天 | 669. 修剪二叉搜索树，108.将有序数组转换为二叉搜索树，538.把二叉搜索树转换为累加树，总结篇
· 代码随想录day22| 二叉搜索树的最近公共祖先 . 二叉搜索树中的插入操作、450. 删除二叉搜索树中的节点
· 代码随想录算法训练营第19天|235. 二叉搜索树的最近公共祖先 ，701.二叉搜索树中的插入操作，450.删除二叉搜索树中的节点
· 代码随想录算法训练营第二十二天 | 235. 二叉搜索树的最近公共祖先，701.二叉搜索树中的插入操作，450.删除二叉搜索树中的节点
阅读排行：
· 全程不用写代码，我用AI程序员写了一个飞机大战
· MongoDB 8.0这个新功能碉堡了，比商业数据库还牛
· 记一次.NET内存居高不下排查解决与启示
· DeepSeek 开源周回顾「GitHub 热点速览」
· 白话解读 Dapr 1.15：你的「微服务管家」又秀新绝活了
点击右上角即可分享
微信分享提示