代码随想录算法训练营第二十天 | 530.二叉搜索树的最小绝对差，501.二叉搜索树中的众数，236. 二叉树的最近公共祖先

一、参考资料

二叉搜索树的最小绝对差

题目链接/文章讲解：https://programmercarl.com/0530.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E7%9A%84%E6%9C%80%E5%B0%8F%E7%BB%9D%E5%AF%B9%E5%B7%AE.html

视频讲解：https://www.bilibili.com/video/BV1DD4y11779

二叉搜索树中的众数

题目链接/文章讲解：https://programmercarl.com/0501.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E4%BC%97%E6%95%B0.html

视频讲解：https://www.bilibili.com/video/BV1fD4y117gp

二叉树的最近公共祖先

题目链接/文章讲解：https://programmercarl.com/0236.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E6%9C%80%E8%BF%91%E5%85%AC%E5%85%B1%E7%A5%96%E5%85%88.html

视频讲解：https://www.bilibili.com/video/BV1jd4y1B7E2

二、LeetCode530.二叉搜索树的最小绝对差

https://leetcode.cn/problems/minimum-absolute-difference-in-bst/description/

示例一：

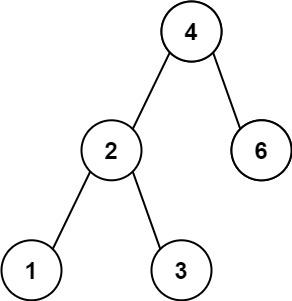
示例二：

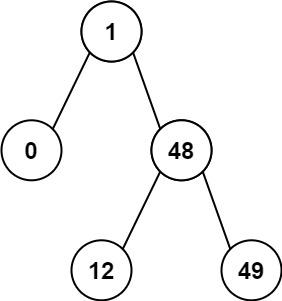
给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数，其数值等于两值之差的绝对值。

示例 1：
输入：root = [4,2,6,1,3] 输出：1
示例 2：
输入：root = [1,0,48,null,null,12,49] 输出：1
提示：
树中节点的数目范围是 [2, 10^4]
0 <= Node.val <= 10^5
注意：本题与 783 https://leetcode-cn.com/problems/minimum-distance-between-bst-nodes/ 相同 
  1. /**
  2.  * Definition for a binary tree node.
  3.  * struct TreeNode {
  4.  *     int val;
  5.  *     TreeNode *left;
  6.  *     TreeNode *right;
  7.  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  8.  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  9.  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  10.  * };
  11.  */
  12. class Solution {
  13. public:
  14.     int res = INT_MAX;
  15.     TreeNode* pre = NULL;   // pre节点记录一下cur节点的前一个节点
  16.     void traversal(TreeNode* cur) {
  17.         if (cur == NULL) return ;
  18.         traversal(cur->left);
  19.         if (pre != NULL) {
  20.             res = min(res, cur->val - pre->val);
  21.         }
  22.         pre = cur;
  23.         traversal(cur->right);
  24.     }
  25.     int getMinimumDifference(TreeNode* root) {
  26.         // 递归法解决
  27.         traversal(root);
  28.         return res;
  29.     }
  30. };

迭代法：

  1. /**
  2.  * Definition for a binary tree node.
  3.  * struct TreeNode {
  4.  *     int val;
  5.  *     TreeNode *left;
  6.  *     TreeNode *right;
  7.  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  8.  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  9.  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  10.  * };
  11.  */
  12. class Solution {
  13. // 迭代——用栈实现二叉树的中序遍历
  14. public:
  15.     int getMinimumDifference(TreeNode* root) {
  16.         stack<TreeNode*> st;
  17.         TreeNode* cur = root;
  18.         TreeNode* pre = NULL;
  19.         int res = INT_MAX;
  20.         while (cur != NULL || !st.empty()) {
  21.             if (cur != NULL) {     // 指针来访问节点，访问到最底层
  22.                 st.push(cur);      // 将访问的节点放进栈
  23.                 cur = cur->left;   // 左
  24.             } else {
  25.                 cur = st.top();
  26.                 st.pop();
  27.                 if (pre != NULL) {
  28.                     res = min(res, cur->val - pre->val);
  29.                 }
  30.                 pre = cur;
  31.                 cur = cur->right;
  32.             }
  33.         }
  34.         return res;
  35.     }
  36. };

卡哥总结：

遇到在二叉搜索树上求什么最值，求差值之类的，都要思考一下二叉搜索树可是有序的，要利用好这一特点。同时要学会在递归遍历的过程中如何记录前后两个指针，这也是一个小技巧，学会了还是很受用的。

三、LeetCode501.二叉搜索树中的众数

https://leetcode.cn/problems/find-mode-in-binary-search-tree/description/

示例1：

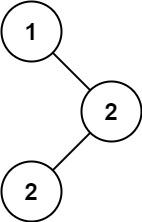
给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。
如果树中有不止一个众数，可以按 任意顺序 返回。
假定 BST 满足如下定义：
结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

示例 1：
输入：root = [1,null,2,2] 输出：[2]
示例 2：
输入：root = [0] 输出：[0]
提示：
树中节点的数目在范围 [1, 104] 内
-105 <= Node.val <= 105

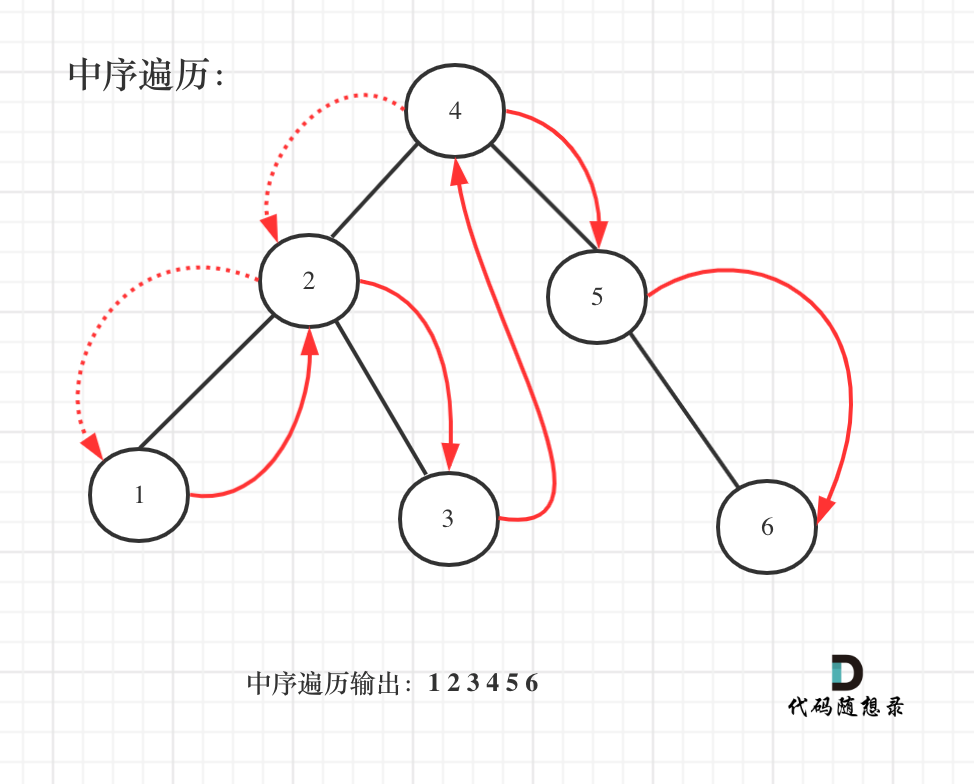
（只需要遍历一遍二叉搜索树，就求出了众数的集合）

  1. // 卡哥代码（详细注释版）
  2. class Solution {
  3. private:
  4.     int maxCount = 0; // 最大频率
  5.     int count = 0; // 统计频率
  6.     TreeNode* pre = NULL;
  7.     vector<int> result;
  8.     void searchBST(TreeNode* cur) {
  9.         if (cur == NULL) return ;
  10.  
  11.         searchBST(cur->left);       // 左
  12.                                     // 中
  13.         if (pre == NULL) { // 第一个节点
  14.             count = 1;
  15.         } else if (pre->val == cur->val) { // 与前一个节点数值相同
  16.             count++;
  17.         } else { // 与前一个节点数值不同
  18.             count = 1;
  19.         }
  20.         pre = cur; // 更新上一个节点
  21.  
  22.         if (count == maxCount) { // 如果和最大值相同，放进result中
  23.             result.push_back(cur->val);
  24.         }
  25.  
  26.         if (count > maxCount) { // 如果计数大于最大值频率
  27.             maxCount = count;   // 更新最大频率
  28.             result.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了
  29.             result.push_back(cur->val);
  30.         }
  31.  
  32.         searchBST(cur->right);      // 右
  33.         return ;
  34.     }
  35.  
  36. public:
  37.     vector<int> findMode(TreeNode* root) {
  38.         count = 0;
  39.         maxCount = 0;
  40.         TreeNode* pre = NULL; // 记录前一个节点
  41.         result.clear();
  42.  
  43.         searchBST(root);
  44.         return result;
  45.     }
  46. };
  1. // version1：普通二叉树，递归法
  2. class Solution {
  3. private:
  4.     // 前序遍历
  5.     void searchBST(TreeNode* cur, unordered_map<int, int>& map) {
  6.         if (cur == NULL) return ;
  7.         map[cur->val]++;
  8.         searchBST(cur->left, map);
  9.         searchBST(cur->right, map);
  10.         return ;
  11.     }
  12.  
  13.     bool static cmp(const pair<int, int>& a, const pair<int, int>& b) {
  14.         return a.second > b.second;
  15.     }
  16.  
  17. public:
  18.     vector<int> findMode(TreeNode* root) {
  19.         unordered_map<int, int> map;   // key: 元素，value：出现频率
  20.         vector<int> res;
  21.         if (root == NULL) return res;
  22.         searchBST(root, map);
  23.         vector<pair<int, int>> vec(map.begin(), map.end());
  24.         sort(vec.begin(), vec.end(), cmp);  // 给频率排序
  25.         res.push_back(vec[0].first);
  26.         for (int i = 1; i < vec.size(); i++) {
  27.             // 取最高的放到res数组中
  28.             if (vec[i].second == vec[0].second) res.push_back(vec[i].first);
  29.             else break;
  30.         }
  31.         return res;
  32.     }
  33. };
  1.  // version2:二叉搜索树，只需要遍历一遍，就求出众数的集合
  2. class Solution {
  3. private:
  4.     int maxCount = 0;  // 最大频率
  5.     int count = 0;     // 统计频率
  6.     TreeNode* pre = NULL;
  7.     vector<int> res;
  8.     
  9.     void searchBST(TreeNode* cur) {
  10.         if (cur == NULL) return ;
  11.         searchBST(cur->left);   // 左
  12.         // 中
  13.         if (pre == NULL) {      // 第一个节点
  14.             count = 1;
  15.         } else if (pre->val == cur->val) {   // 与前一个节点数值相同
  16.             count ++;
  17.         } else {  // 与前一个节点数值不同
  18.             count = 1;
  19.         }
  20.         pre = cur;  // 更新上一个节点
  21.  
  22.         // 如果和最大值相同，放进result中
  23.         if (count == maxCount) {
  24.             res.push_back(cur->val);
  25.         }
  26.         // 如果计数大于最大值频率
  27.         if (count > maxCount) {
  28.             maxCount = count;   // 更新最大频率
  29.             res.clear();        // 很关键的一步，不要忘记清空Result数组
  30.             res.push_back(cur->val);
  31.         }
  32.  
  33.         searchBST(cur->right);   // 右
  34.     }
  35.  
  36. public:
  37.     vector<int> findMode(TreeNode* root) {
  38.         count = 0;
  39.         maxCount = 0;
  40.         TreeNode* pre = NULL;  // 记录前一个节点
  41.         res.clear();
  42.  
  43.         searchBST(root); 
  44.         return res;
  45.     }
  46. };
  1. // 我写的，简化版
  2. class Solution {
  3. private:
  4.     vector<int> res;
  5.     int count = 0;
  6.     int maxCount = 0;
  7.     TreeNode* pre = NULL;
  8.  
  9.     void searchBST(TreeNode* cur) {
  10.         if (cur == NULL) return ;
  11.         searchBST(cur->left);
  12.         if (pre == NULL) count = 1;
  13.         else if (pre->val == cur->val) count++;
  14.         else count = 1;
  15.         pre = cur;   // 更新pre ！！！很重要
  16.         // 这里一定不能合并下面的两个if，假如和原来相等的count，那么clear操作会清楚原来的数值
  17.         if (count == maxCount) res.push_back(cur->val);
  18.         if (count > maxCount) {
  19.             maxCount = count;
  20.             res.clear();
  21.             res.push_back(cur->val);
  22.         }
  23.  
  24.         searchBST(cur->right);
  25.     }
  26.  
  27. public:
  28.     vector<int> findMode(TreeNode* root) {
  29.         searchBST(root);
  30.         return res;
  31.     }
  32. };

迭代法：

  1. // version3: 迭代法
  2. class Solution {
  3. public:
  4.     vector<int> findMode(TreeNode* root) {
  5.         stack<TreeNode*> st;
  6.         TreeNode* cur = root;
  7.         TreeNode* pre = NULL;
  8.         vector<int> res;
  9.         int count = 0;
  10.         int maxCount = 0;
  11.  
  12.         while (cur != NULL || !st.empty()) {
  13.             if (cur != NULL) {
  14.                 st.push(cur);
  15.                 cur = cur->left;
  16.             } else {
  17.                 cur = st.top();
  18.                 st.pop();
  19.                 if (pre == NULL) count = 1;
  20.                 else if (pre->val == cur->val) count++;
  21.                 else count = 1;
  22.                 pre = cur;
  23.                 if (count == maxCount) {
  24.                     res.push_back(cur->val);
  25.                 }
  26.                 if (count > maxCount) {
  27.                     maxCount = count;
  28.                     res.clear();
  29.                     res.push_back(cur->val);
  30.                 }
  31.                 cur = cur->right;
  32.             }
  33.         }
  34.         return res;
  35.     }
  36. };

后面我又分别用递归和迭代独立实现了一遍~代码就不贴了

四、LeetCode236. 二叉树的最近公共祖先

https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/description/

示例一：

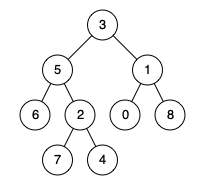
示例二：

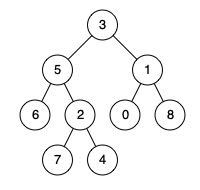
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（ 一个节点也可以是它自己的祖先）。”

示例 1：
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：
输入：root = [1,2], p = 1, q = 2 输出：1
提示：
树中节点数目在范围 [2, 10^5] 内。
-10^9 <= Node.val <= 10^9
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。 
  1. // 我根据视频讲解思路理解写的代码：
  2. /**
  3.  * Definition for a binary tree node.
  4.  * struct TreeNode {
  5.  *     int val;
  6.  *     TreeNode *left;
  7.  *     TreeNode *right;
  8.  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  9.  * };
  10.  */
  11. class Solution {
  12. public:
  13.     TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
  14.         if (root == NULL || root == p || root == q) return root;
  15.         TreeNode* left = lowestCommonAncestor(root->left, p, q);
  16.         TreeNode* right = lowestCommonAncestor(root->right, p, q);
  17.  
  18.         if (left != NULL && right != NULL) return root;
  19.         else if (left == NULL && right != NULL) return right;
  20.         else if (left != NULL && right == NULL) return left;
  21.         else return NULL;
  22.     }
  23. };

在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

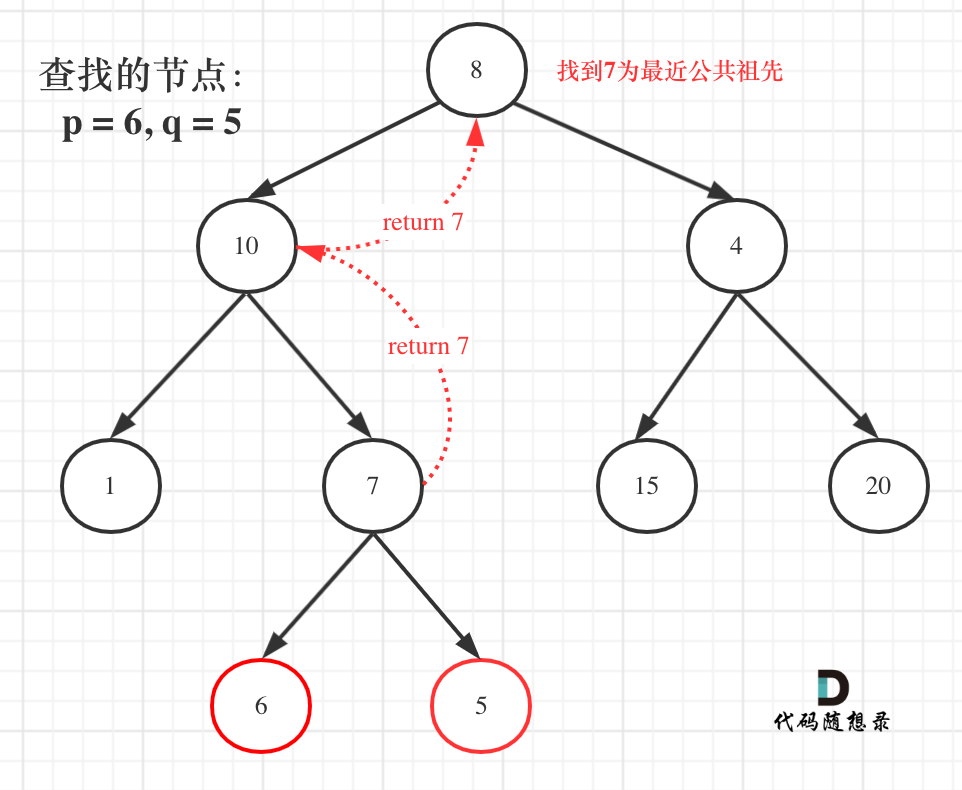
如果left 和 right都不为空，说明此时root就是最近公共节点。这个比较好理解

如果left为空，right不为空，就返回right，说明目标节点是通过right返回的，反之依然。

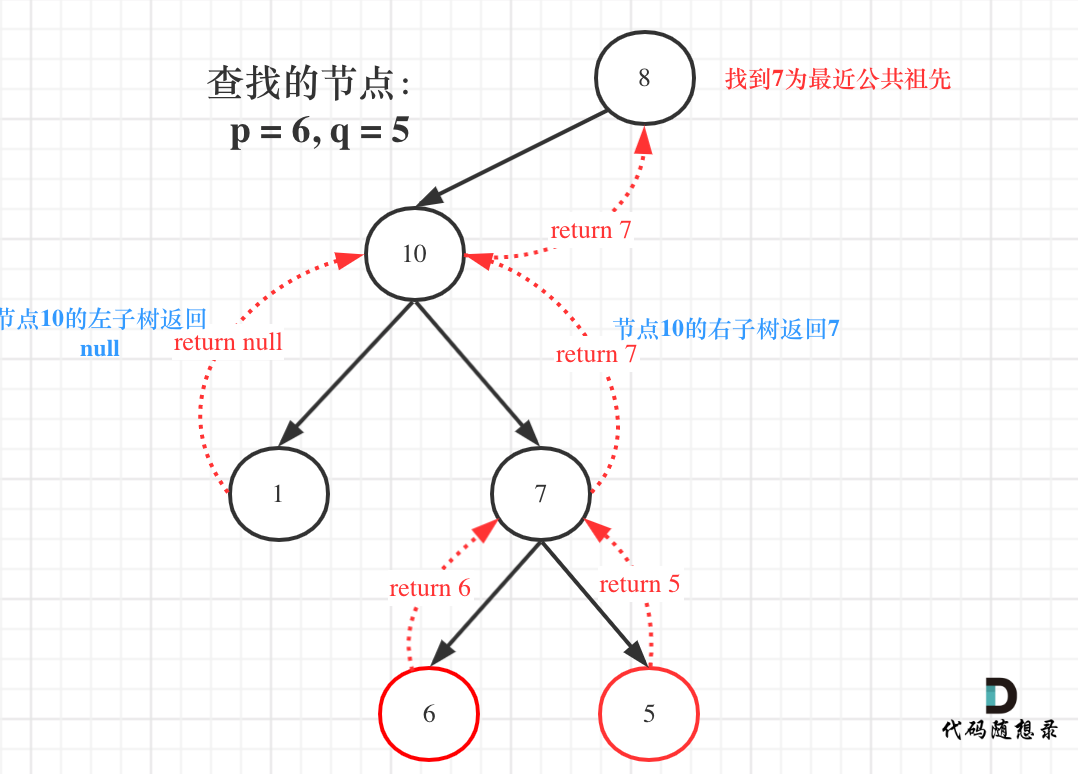
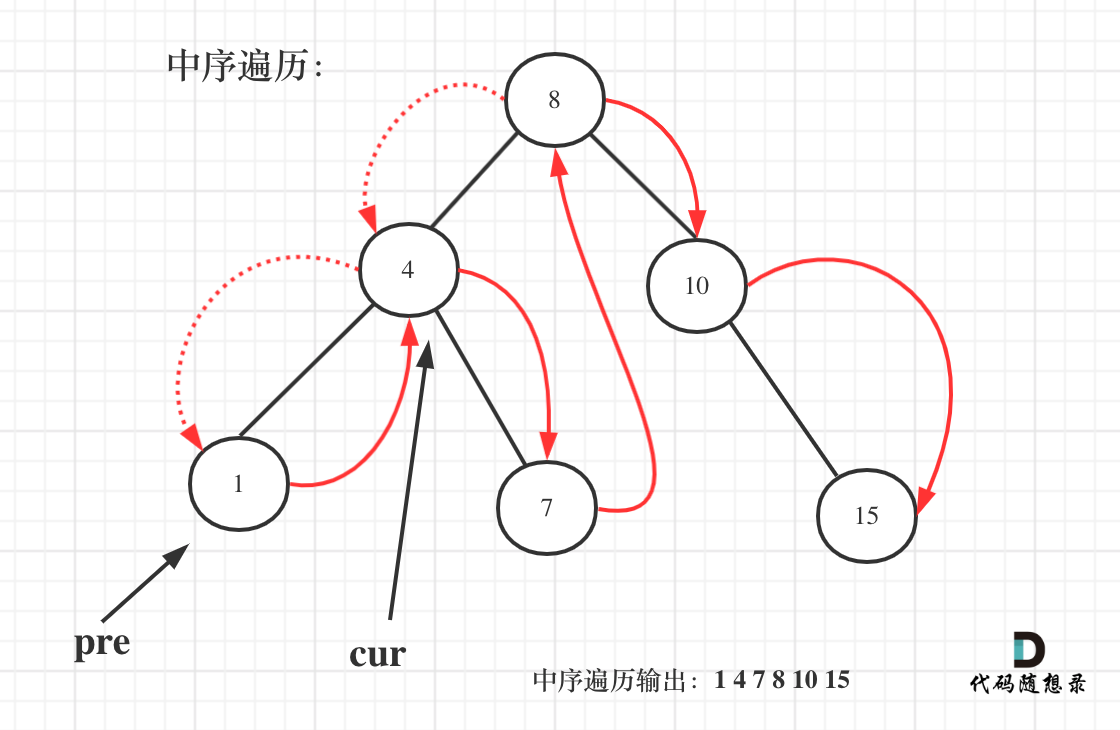
图中节点10的左子树返回null，右子树返回目标值7，那么此时节点10的处理逻辑就是把右子树的返回值（最近公共祖先7）返回上去！

这里也很重要，可能刷过这道题目的同学，都不清楚结果究竟是如何从底层一层一层传到头结点的。

那么如果left和right都为空，则返回left或者right都是可以的，也就是返回空。

寻找最小公共祖先，完整流程图如下：

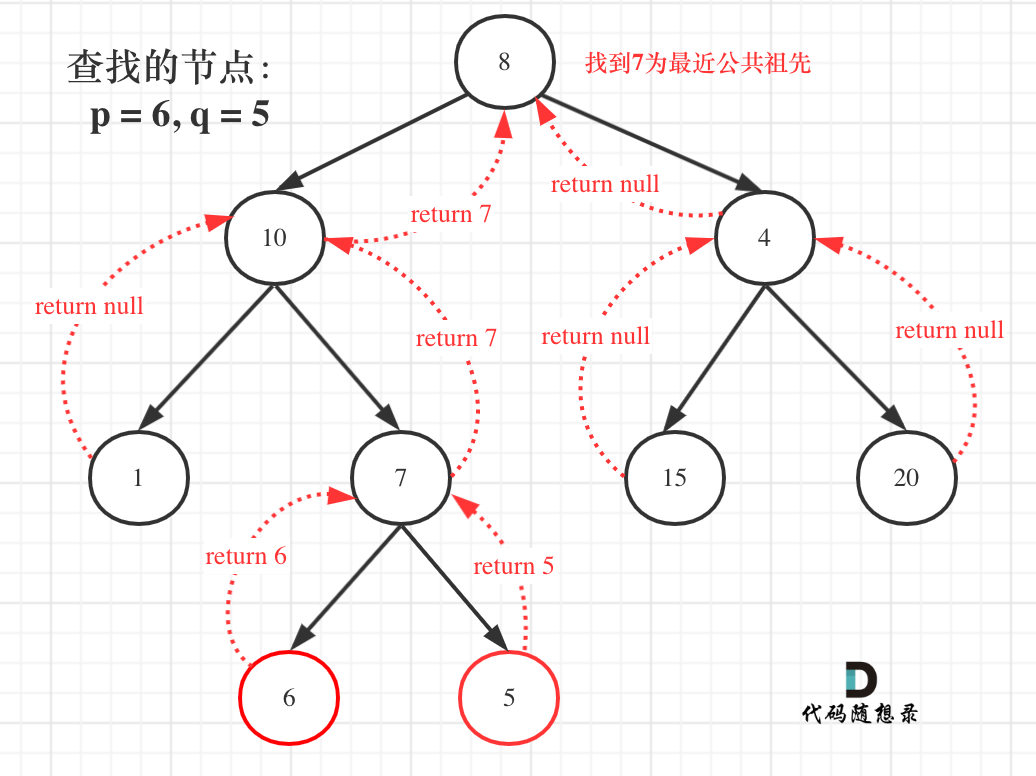
  1. // 精简版
  2. class Solution {
  3. public:
  4.     TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
  5.         if (root == q || root == p || root == NULL) return root;
  6.         TreeNode* left = lowestCommonAncestor(root->left, p, q);
  7.         TreeNode* right = lowestCommonAncestor(root->right, p, q);
  8.         if (left != NULL && right != NULL) return root;
  9.         if (left == NULL) return right;
  10.         return left;
  11.     }
  12. };

卡哥总结：对回溯的理解，以及结果是如何一层一层传递上去的，有三点归纳：

  1. 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从底向上的遍历方式。

  1. 在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。

  1. 要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。

最后，本题没有给出迭代法，因为迭代法不适合模拟回溯的过程。

总结：

状态还不错哈，对递归和回溯有了更多的认识，多复习哈，还有就是记得看自己写的一些注释。

昨天补完了三天的题，今天补完所有博客，再把最后一节树的题目做完，争取完结撒花~

刷题加油鸭~~

posted @ 2023-02-05 16:54  ZYM-爱吃柚子的程序媛  阅读(453)  评论(0)    收藏  举报