CS231n作业(二):卷积神经网络基础

CS231n作业(二):卷积神经网络

​ 这个作业完成的很快，但是这里面的内容是非常重要的，知识点挺多，写一篇文章来记录下。这个作业里面的许多的内容，在课程中都没有仔细的讲解，很多点自己推导的话要费点时间(其实自己推导挺好的)，为了快速理解里面的知识点，也查找了许多的资料，这篇博客的目的就是将一些细碎的知识点串起来，这里也会包含一些重要的知识点，若已经掌握了可以跳过。写这个博客算是一种复习方式吧(应该没多少人会看到这个博客，雾🙃)。

​ 在这篇博客中会给出部分代码的实现，但还是不看这些实现，凭借思想再写一遍好。个人的领悟能力有限，必定有理解不透彻的部分，错误的部分，如果真有同学发现了这篇博客，找到了一些错误，请在评论区指出。

目录

看见右下角那个图标没？那三个点的就是目录(😓)

Part1:Fully-connected Neural Network

上一个作业中，我们已经实现了一个二层的全连接网络，但是并不是模块化的，使用不便，这里作业要求我们实现一个模块化的全连接网络，这些模块贯穿整个作业，都会被用到。这里需要注意:每一次的操作都要清楚是什么样的维度的矩阵在相乘，这几个维度的具体的意义是什么?

Affine layer

前向传播:注意给出的\(x,w,b\)的维度，直接相乘就可以了。

#  初始化矩阵大小，便于计算
    N = x.shape[0]
    d_i = x.shape[1:]
    D = np.prod(d_i)  # np.prod是各项的乘积
    X = x.reshape((N, D))
    out = X @ w + b

反向传播:类似于线性的\(y=wX+b\) 这里求法一致，只是这里要注意的一点就是维度是否相容，是否需要把某一个矩阵转置。Trick:把bias的这个偏置项放到\(w\)中,可以使计算更加简洁。

#  add bias to W and X to make calculate easier
    N = x.shape[0]
    d_i = x.shape[1:]
    D = np.prod(d_i)
    X = x.reshape((N, D))

    length_W = len(b)
    X = np.c_[X, np.ones((N, 1), dtype=np.float64)]
    W = np.r_[w, b.reshape(1, length_W)]
    # calculate gradient
    d_x = dout @ W.T
    d_w = X.T @ dout
    #  return
    dx = d_x[:, :-1]
    dw = d_w[:-1, :]
    db = d_w[-1, :]
    dx = dx.reshape(x.shape)

ReLU

前向传播:前向传播非常简单，只是单纯的与0做比较。

反向传播:在这里只传递在前向传播中不为0的项，其梯度为1(\(dout\)),其余小于0的梯度都是0

Loss

这个之前已经做过了，可以看一下博客里的svm与softmax那一篇

Two-layer network

这里的结构是affine-->relu-->affine-->softmax具体的框架基本上都已经给出了，稍微看下layer_utils中的封装就可写出来，网络结构没出错基本上不会有问题。在num_epoch=10,lr=1e-3,lr_decay=0.9下正确率是\(52.8\%\)左右。

Multilayer network

这里的结构是{affine-->[BN]-->relu-->[dropout]}-->affine--> softmax可以考虑在加上BN层和dropout层，如果加上了，最好在layer_utils里面写一个封装。这里的BN和dropout在之后的作业里讲解。这边部分也没有什么理解上的难点，看下作业里的注释应该可以解决。

---

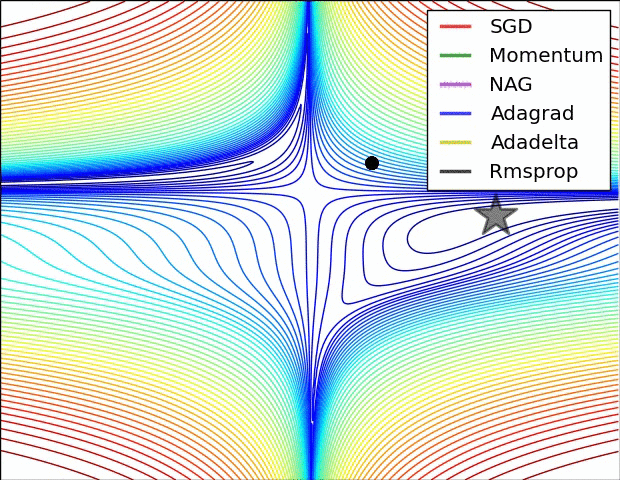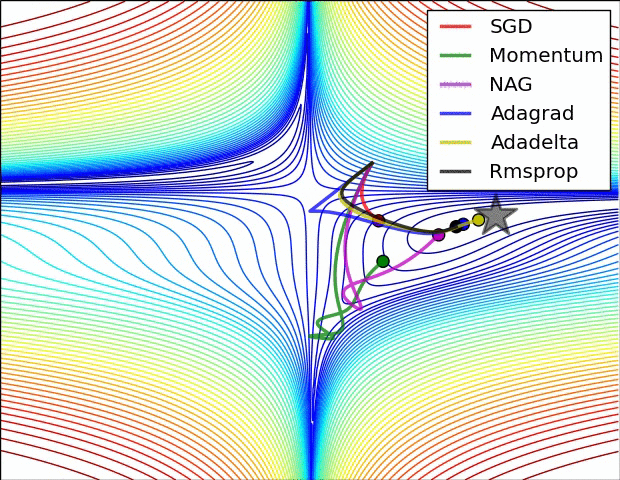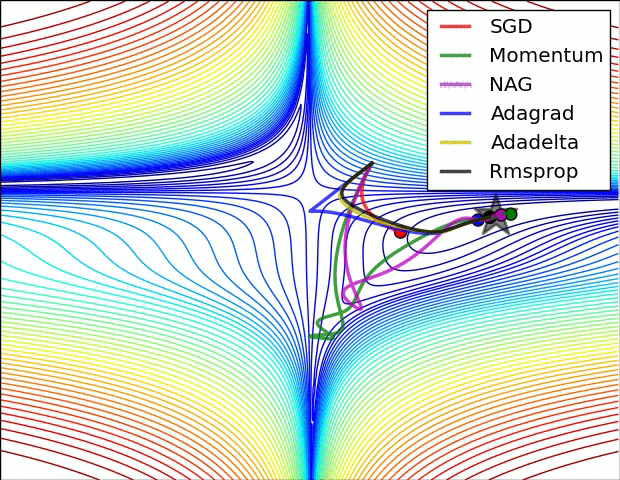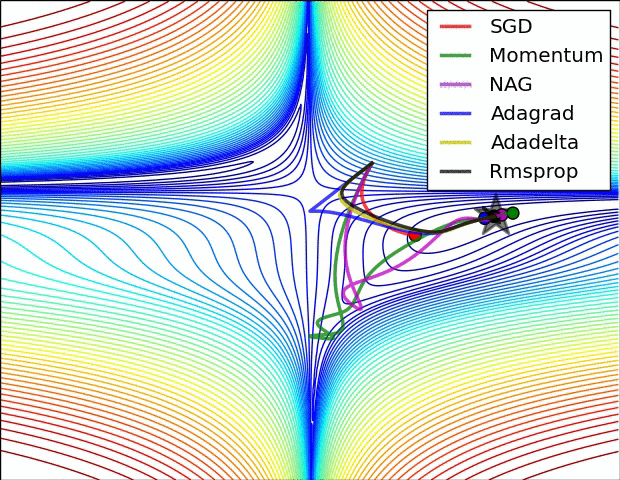
接下来是几个比较重要的优化器。这里记录下知识点与 trick.

接下来是几个比较重要的优化器。这里记录下知识点与 trick.

这里记录的比较细，部分内容与作业无关，可以跳过。下文知识点大部分引自翻译文档

官方的文档,翻译文档

SGD+Momentum

在普通版本中，梯度直接影响位置。而在这个版本的更新中，物理观点建议梯度只是影响速度，然后速度再影响位置.在这里引入了一个初始化为0的变量v和一个超参数mu。说得不恰当一点，这个变量（mu）在最优化的过程中被看做动量（一般值设为0.9），但其物理意义与摩擦系数更一致。这个变量有效地抑制了速度，降低了系统的动能，不然质点在山底永远不会停下来。通过交叉验证，这个参数通常设为[0.5,0.9,0.95,0.99]中的一个。

我们可以得到以下的表达式(\(SGD+Momentum\)):

\[\begin{cases} V_{t+1}=\rho V_T+\nabla f(x_t)\newline x_{t+1}=x_t-\alpha V_t + 1 \end{cases} \]

在这里初始时动量为0，当\(\rho\)为0时其实就是普通的SGD

v = mu * v - learning_rate * dx # 与速度融合
x += v # 与位置融合

SGD+Nesterov

Nesterov动量与普通动量有些许不同，最近变得比较流行。在理论上对于凸函数它能得到更好的收敛，在实践中也确实比标准动量表现更好一些。Nesterov动量的核心思路是，当参数向量位于某个位置x时，观察上面的动量更新公式可以发现，动量部分（忽视带梯度的第二个部分）会通过mu * v稍微改变参数向量。因此，如果要计算梯度，那么可以将未来的近似位置x + mu * v看做是“向前看”，这个点在我们一会儿要停止的位置附近。因此，计算x + mu * v的梯度而不是“旧”位置x的梯度就有意义了。

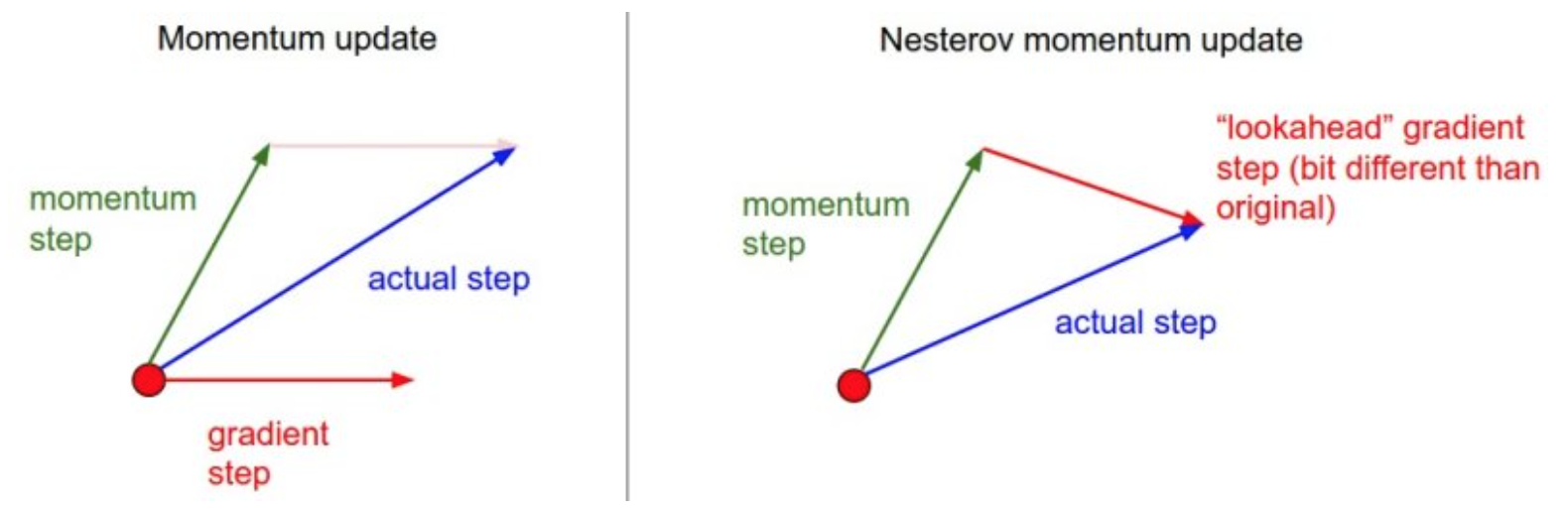
Nesterov动量。既然我们知道动量将会把我们带到绿色箭头指向的点，我们就不要在原点（红色点）那里计算梯度了。使用Nesterov动量，我们就在这个“向前看”的地方计算梯度。

[在作业里如此实现：]

v = config['momentum'] * v - config['learning_rate'] * dw   # Nesterov Momentum
next_w = w + v

Adagrad

这个优化的主要思想就是使用一个惩罚项来使梯度的更新变化，但是缺点明显，这个更新方式最终会使下面代码中描述的分母越来越大最终导致更新量越来越小，最后可能不会更新

grad_squared=0
while True:
	dx = compute_gradient(x)
	grad_squared += dx*dx
	x -= learning_rate*dx/(np.sqrt(grad_squared)+1e-7)

RMSProp：“Leaky Adagrad”

这个方法用一种很简单的方式修改了Adagrad方法，让它不那么激进，单调地降低了学习率。具体说来，就是它使用了一个梯度平方的滑动平均。

grad_squared=0
while True:
	dx = compute_gradient(x)
	grad_squared = deacy_rate*grad_squared+(1-decay_rate)*dx*dx
	x -= learning_rate*dx/(np.sqrt(grad_squared)+1e-7)

decay_rate是一个超参数，常用的值是[0.9,0.99,0.999]。RMSProp仍然是基于梯度的大小来对每个权重的学习率进行修改，这同样效果不错。但是和Adagrad不同，其更新不会让学习率单调变小。

[在作业里如此实现：]

decay_rate = config['decay_rate']
config['cache'] = decay_rate * config['cache'] + (1 - decay_rate) * (dw * dw)
next_w = w - config['learning_rate'] * dw / (np.sqrt(config['cache']) +config['epsilon'])  # epsilon~1e7

Adam

Adam是最近才提出的一种更新方法，它看起来像是RMSProp的动量版。简化的代码是下面这样：

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)

注意这个更新方法看起来真的和RMSProp很像，除了使用的是平滑版的梯度m，而不是用的原始梯度向量dx。论文中推荐的参数值eps=1e-8, beta1=0.9, beta2=0.999。在实际操作中，我们推荐Adam作为默认的算法，一般而言跑起来比RMSProp要好一点。但是也可以试试SGD+Nesterov动量。完整的Adam更新算法也包含了一个偏置（bias）矫正机制，因为m,v两个矩阵初始为0，在没有完全热身之前存在偏差，需要采取一些补偿措施,如下：

first_moment=0
second_moment=0
for t in range(a,num_iterations):
    dx = compute_gradient(x)
    first_moment=beta1*first_moment+(1-beta1)*dx
    second_moment=beta2*second_moment+(1-beta2)*dx*dx
    first_unbias=first_moment/(1-beta1**t)  # 这里通过这个操作使初始值较高
    sec同上
    x-=同上

[在作业里如此实现：]

config['t'] += 1
config['m'] = config['beta1'] * config['m'] + (1 - config['beta1']) * dw
config['v'] = config['beta2'] * config['v'] + (1 - config['beta2']) * (dw * dw)
m_hat = config['m'] / (1 - config['beta1'])  # 为了使beta快速得到一个合适的值，来加快训练的速度
v_hat = config['v'] / (1 - config['beta2'])
next_w = w - config['learning_rate'] * m_hat / (np.sqrt(v_hat) + config['epsilon'])

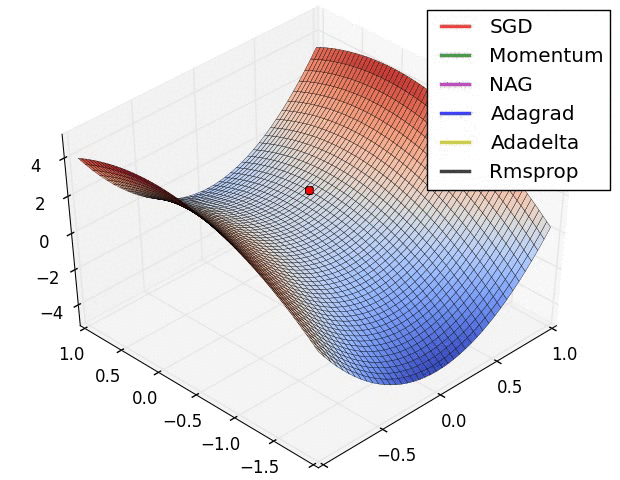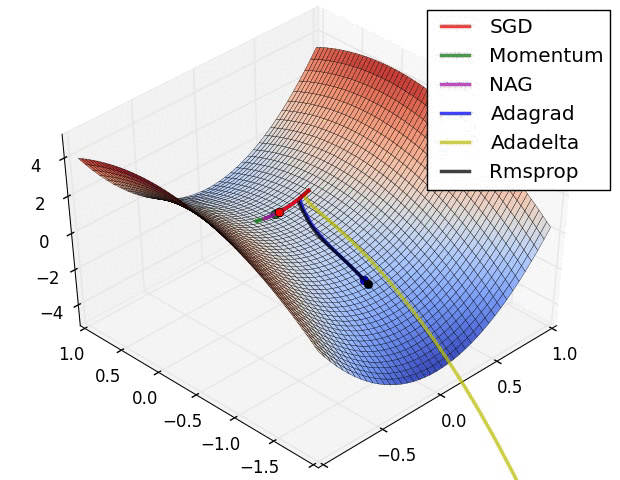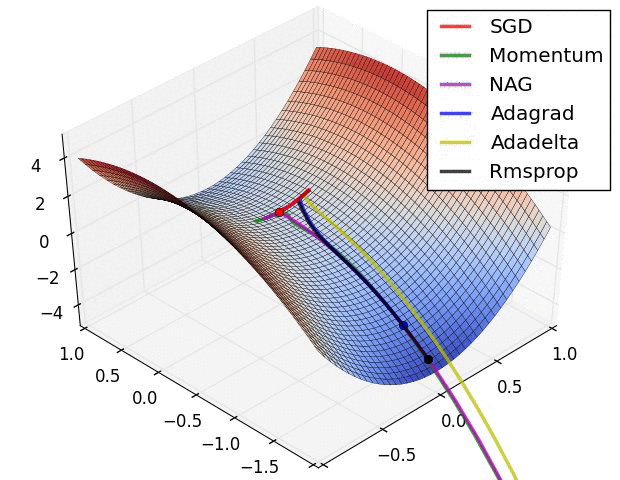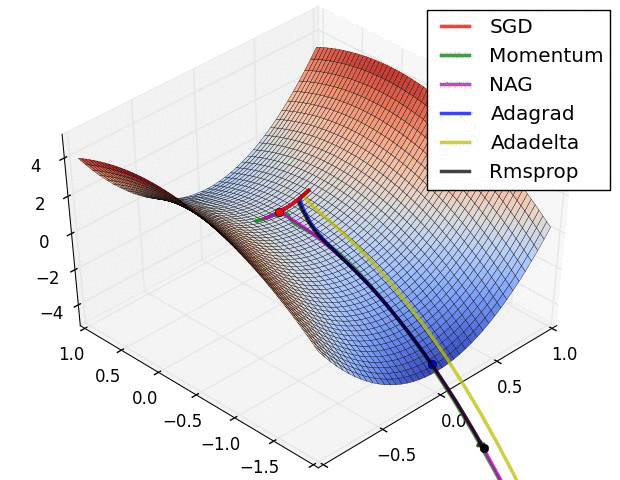
Part2:Batch Normalization

在这个章节碰到了伟大的BN，魔法般的BN。作业里需要我们实现前向传播，反向传播，并运用BN层，一些BN的细节放在下文中的杂项里，这里讨论作业中遇到的。

前向传播

如果想要深入理解：论文 :Batch Normalization

首先祭出这张图:(按照图上来绝对没错，bushi👍)

# train
sample_mean = np.mean(x, axis=0)
sample_var = np.var(x, axis=0)
mean = (x - sample_mean)
norm = 1 / np.sqrt(sample_var + eps)
x_hat = mean * norm

running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var

out = gamma * x_hat + beta
cache = (x, x_hat, gamma, norm, mean, sample_var, eps)
# test
x_hat = (x - running_mean) / np.sqrt(running_var + eps)  # epsilon
out = gamma * x_hat + beta

这里遇到的一个问题就是:测试的时候没有minibatch,怎么来计算均值和方差呢？这里我们的解决方案是通过使用基于momentum的指数衰减，从而估计出均值和方差。

反向传播

反向传播是基于链式法则的，论文中具体的公式如下:

\[\begin {align} &\frac {\partial \ell}{\partial \hat x_i} = \frac {\partial \ell} {\partial y_i} \cdot \gamma\\ &\frac {\partial \ell}{\partial \sigma_\cal B^2} = \sum_{i=1}^m \frac {\partial \ell}{\partial \hat x_i}\cdot(x_i-\mu_\cal B)\cdot \frac {-1}{2}(\sigma_\cal B^2+\epsilon)^{-3/2}\\ &\frac {\partial \ell}{\partial \mu_\cal B} = \sum_{i=1}^m \frac {\partial \ell}{\partial \hat x_i}\cdot \frac {-1} {\sqrt {\sigma_\cal B^2 + \epsilon}}\\ &\frac {\partial \ell}{\partial x_i} = \sum_{i=1}^m \frac {\partial \ell}{\partial \hat x_i} \cdot \frac {-1} {\sqrt {\sigma_\cal B^2 + \epsilon}} + \frac {\partial \ell}{\partial \sigma_\cal B^2} \cdot \frac {2(x_i - \mu_\cal B)} {m} + \frac {\partial \ell} {\partial \mu_\cal B} \cdot \frac {1} {m}\\ &\frac {\partial \ell}{\partial \gamma} = \sum_{i=1}^m \frac {\partial \ell}{\partial y_i} \cdot \hat x_i \\ &\frac {\partial \ell}{\partial \beta} = \sum_{i=1}^m \frac {\partial \ell}{\partial y_i} \end{align} \]

根据这个公式一步步写就可

N = dout.shape[0]
x, x_hat, gamma, norm, mean, sample_var, eps = cache
dbeta = np.sum(dout, axis=0)
dgamma = np.sum(dout * x_hat, axis=0)
dx_hat = dout * gamma
dsample_mean = np.sum(dx_hat * (-norm), axis=0)
dsample_var = np.sum((dx_hat * mean * (-1 / 2) * (sample_var + eps) ** (-3 / 2)), axis=0)
dx = dx_hat * norm + dsample_mean * (1.0 / N) + dsample_var * ((2.0 / N) * (mean))

注意这里的beta 和 gamma是一维的这里用了sum加和。那么这个是按照计算图的思想做出来的，还可以用公式直接计算。计算图的BN方法可以具体看这个BN计算详解

接下来的BN作业是应用和比对，没什么可说的。

Part3 Dropout

肝了如此之久，最简单的部分来了(bushi)，这是个迷幻操作，迷幻解释的操作。但实现是简单。

深入理解:[论文](Dropout: A Simple Way to Prevent Neural Networks from Overfitting)

前向传播：

前向传播非常简单，主要注意的就是一个小的trick

普通版本的有：

""" 普通版随机失活: 不推荐实现 (看下面笔记) """
p = 0.5 # 激活神经元的概率. p值更高 = 随机失活更弱
def train_step(X):
  """ X中是输入数据 """
  # 3层neural network的前向传播
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = np.random.rand(*H1.shape) < p # 第一个随机失活遮罩
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = np.random.rand(*H2.shape) < p # 第二个随机失活遮罩
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  # 反向传播:计算梯度... (略)
  # 进行参数更新... (略)
def predict(X):
  # 前向传播时模型集成
  H1 = np.maximum(0, np.dot(W1, X) + b1) * p # 注意：激活数据要乘以p
  H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # 注意：激活数据要乘以p
  out = np.dot(W3, H2) + b

在上面的代码中，train_step函数在第一个隐层和第二个隐层上进行了两次随机失活。在输入层上面进行随机失活也是可以的，为此需要为输入数据X创建一个二值的遮罩。反向传播保持不变，但是肯定需要将遮罩\(U1\)和\(U2\)加入进去。对于这里为什么要乘上\(p\),做如此解释:假设\(x,y\)节点共同指向了\(a\)节点\(x->a\)权重为\(w1\)另一个权重为\(w2\)，且\(p=0.5\)，那么在测试的时候\(E[a]=w_1x+w_2y,E[a]=w_1x+w_2y\)，但是在训练的时候:\(E[a]=\frac{1}{4}(w_1x+w_2y)+\frac{1}{4}(w_1x+0y)+\frac{1}{4}(0x+0y)+\frac{1}{4}(0x+w_2y)=\frac{1}{2}(w_1x+w_2y)\)这里多出了\(\frac{1}{2}\)故乘上来符合训练集，下文中是除以来符合测试集。

注意：在predict函数中不进行随机失活，但是对于两个隐层的输出都要乘以\(p\)，调整其数值范围。这一点非常重要，因为在测试时所有的神经元都能看见它们的输入，因此我们想要神经元的输出与训练时的预期输出是一致的。以\(p=0.5\)为例，在测试时神经元必须把它们的输出减半，这是因为在训练的时候它们的输出只有一半。为了理解这点，先假设有一个神经元\(x\)的输出，那么进行随机失活的时候，该神经元的输出就是\(px+(1−p)0\)，这是有\(1−p\)的概率神经元的输出为0。在测试时神经元总是激活的，就必须调整\(x−>xp\)来保持同样的预期输出。在测试时会在所有可能的二值遮罩（也就是数量庞大的所有子网络）中迭代并计算它们的协作预测，进行这种减弱的操作也可以认为是与之相关的。(这里部分解释从某位神犇处看到的，出处没找到……😓)

上述操作不好的性质是必须在测试时对激活数据要按照\(p\)进行数值范围调整。既然测试性能如此关键，实际更倾向使用反向随机失活（inverted dropout），它是在训练时就进行数值范围调整，从而让前向传播在测试时保持不变。这样做还有一个好处，无论你决定是否使用随机失活，预测方法的代码可以保持不变。反向随机失活的代码如下：

""" 
反向随机失活: 推荐实现方式.
在训练的时候drop和调整数值范围，测试时不做任何事.
"""

p = 0.5 # 激活神经元的概率. p值更高 = 随机失活更弱

def train_step(X):
  # 3层neural network的前向传播
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = (np.random.rand(*H1.shape) < p) / p # 第一个随机失活遮罩. 注意/p!
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = (np.random.rand(*H2.shape) < p) / p # 第二个随机失活遮罩. 注意/p!
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3

  # 反向传播:计算梯度... (略)
  # 进行参数更新... (略)

def predict(X):
  # 前向传播时模型集成
  H1 = np.maximum(0, np.dot(W1, X) + b1) # 不用数值范围调整了
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  out = np.dot(W3, H2) + b

Part4 造个CNN轮子

首先再祭出一张图，这个是理解的关键:

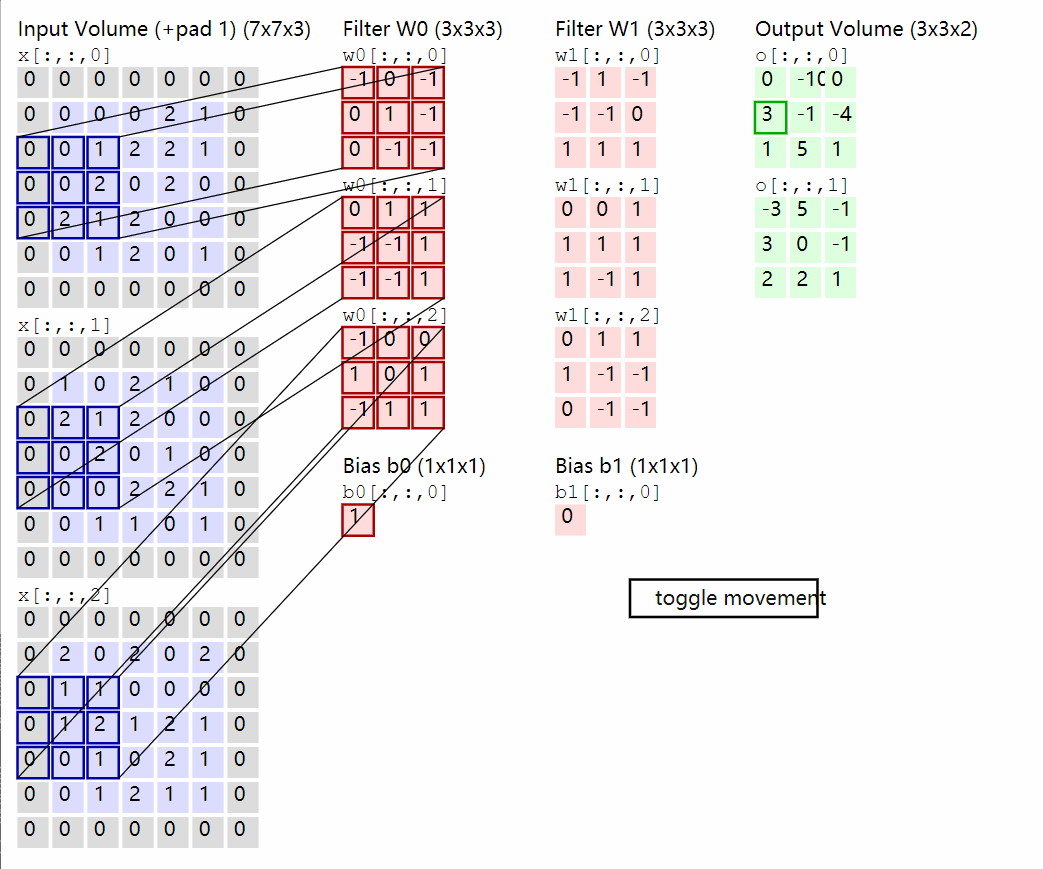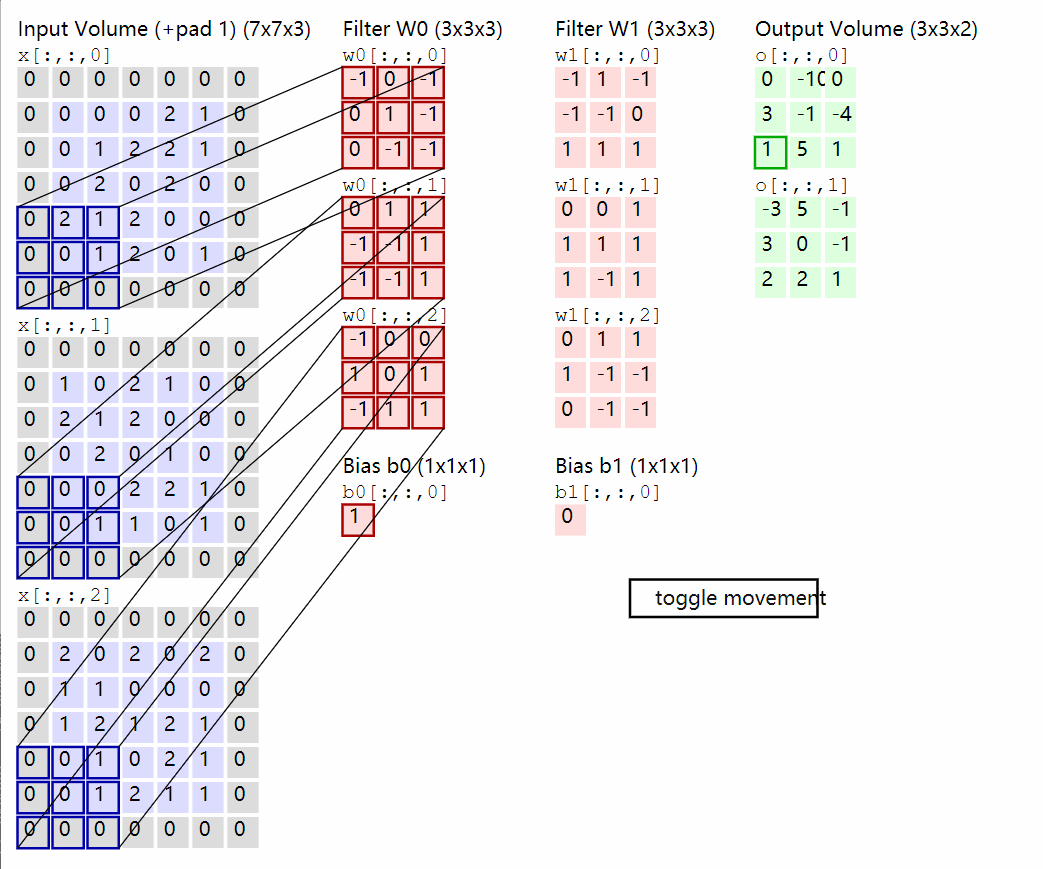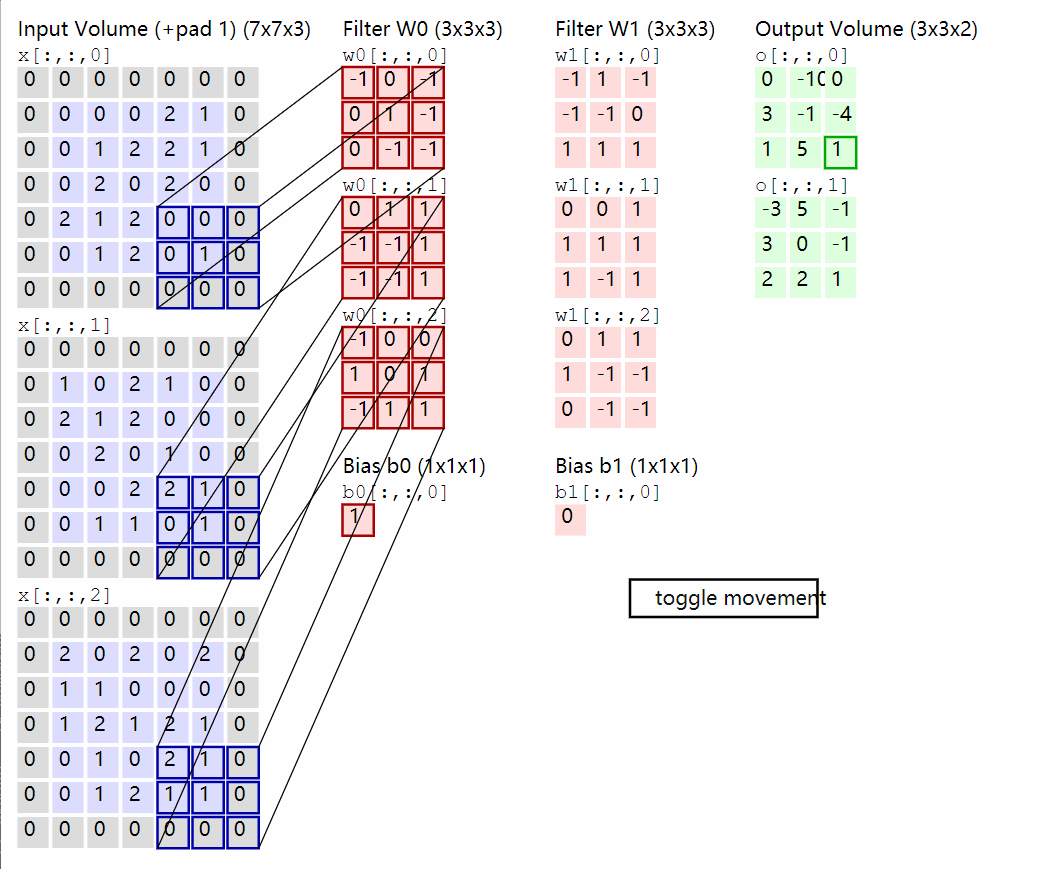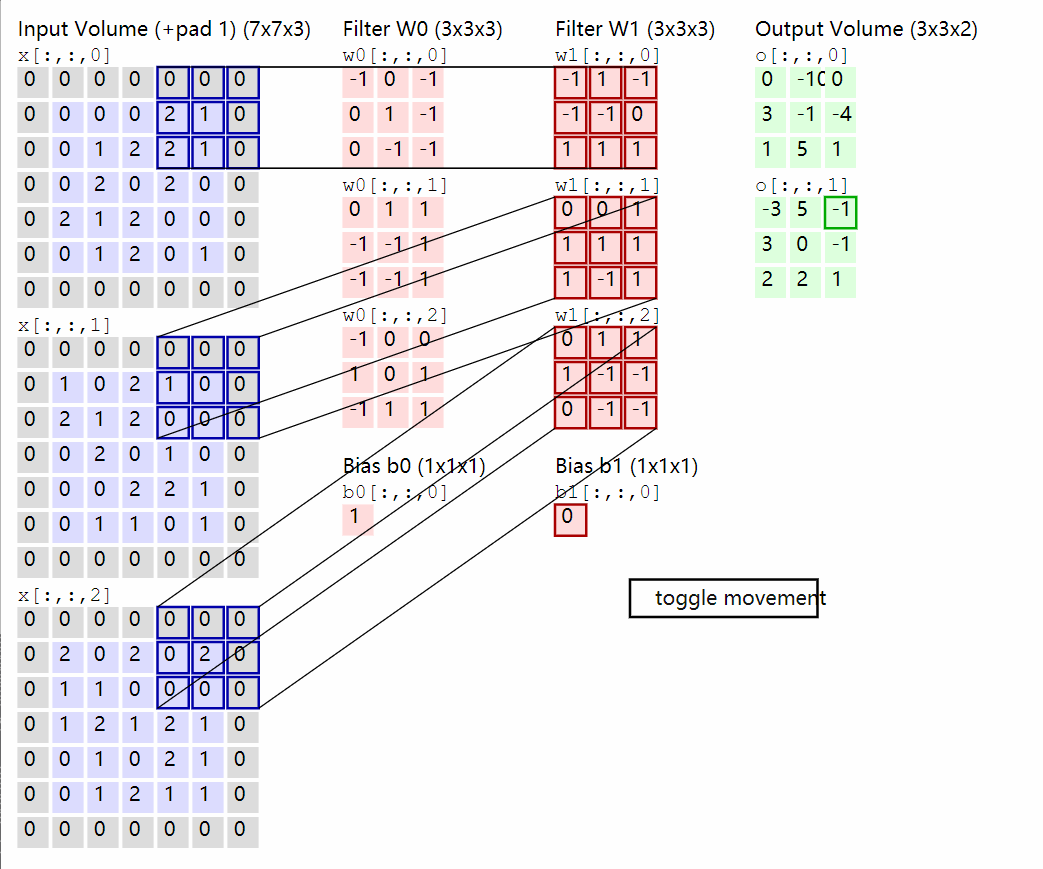
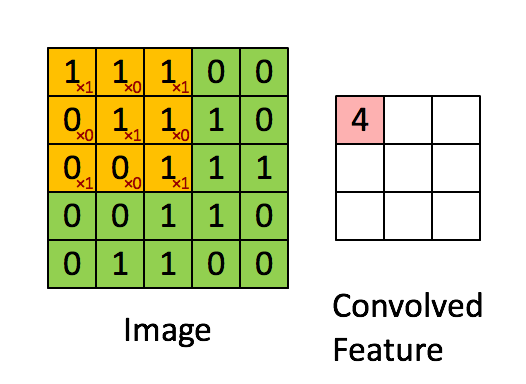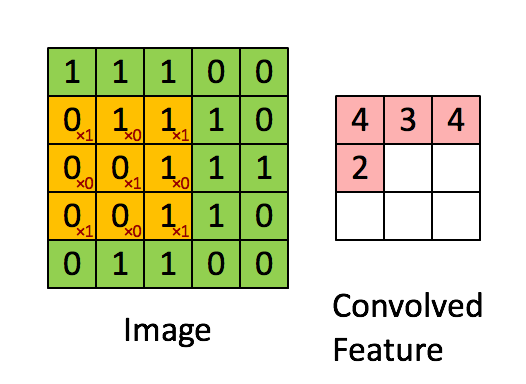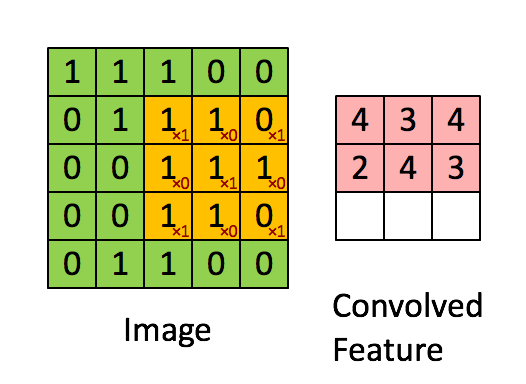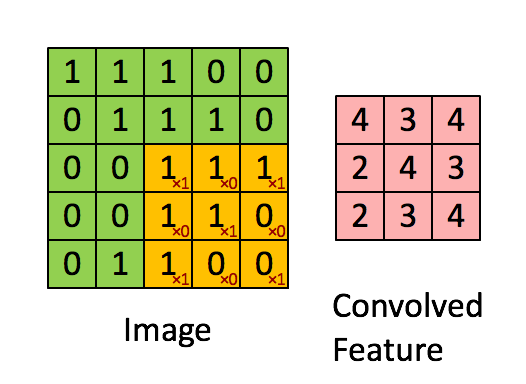
前向传播：

先明确各个维度意义，大小，对于卷积核有F,C,HH,WW = w.shape其中F为卷积核的数量，C为单个卷积核的通道数，HH为高，WW为宽N,C,H,W = x.shape其中N为样本量，C为通道数，H为高，W为宽。还有stride与pad

- conv_param: A dictionary with the following keys:
      - 'stride': The number of pixels between adjacent receptive fields in the
        horizontal and vertical directions.
      - 'pad': The number of pixels that will be used to zero-pad the input.

根据课堂中的公式，我们可以计算出卷积操作后的矩阵的大小

\[H_i=\frac{H-HH+2*Pad}{Stride}+1(W_i同理) \]

我们可以使用nmupy的pad操作来实现Padding操作

numpy.pad(array, pad_width, mode='constant', **kwargs)

可以查看官方文档关于pad的用法

x_paded = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant',constant_values=(0, 0))

卷积操作如上面的动图，我们取每个通道的卷积核与对应通道的X相乘，这里是单个元素相乘，然后求和。

x_i_slice = x_i[:, h_new * stride:h_new * stride + HH, w_new * stride:w_new * stride +WW]
out[i, j, h_new, w_new] = np.sum(x_i_slice * w_j) + b[j]

反向传播:

首先我们需要求\(dx,db,dw\),对于反向传播的解释看这篇博客.

Pooling

同反向传播中那篇博客

接下来就是一些实现，比较简单。

杂项

对于BN的解释博客