无向图三/四元环计数
这么 trivial 的东西竟然学了我一天
首先先抛个定义:
- 无向图 \(k\) 元环:一个无向图 \(k\) 元环指无向图中某个大小为 \(k\) 的边集 \(E=\{e_1,e_2,\cdots,e_k\}\),满足 \(v_{e_i}=u_{e_{i+1}},e_{k+1}=e_1\)(注意,这里的环是针对边集而言的,即对于一个四阶完全图而言,\(1\to 2\to 3\to 4\to 1\) 和 \(1\to 2\to 4\to 3\to 1\) 算两个不同的四元环)
无向图五元环及以上似乎不能在低于 \(m^2\) 的时间内求出?那咱们就不用管它们了。
针对如何求无向图三、四元环的个数,我们考虑一个根分的思想:将无向图的边集重新定向,对于两个存在边相连的点 \(u,v\),我们强制令度数小的点连向度数大的点,当然如果两个点度数一样,那么为了保证这 \(n\) 个点形成严格的偏序关系,我们令编号小的点连向编号大的点。
那么得到的这张图有一个非常好的性质:每个点的出度(注意是出度,至于入度——那没有任何性质)是 \(\mathcal O(\sqrt{m})\) 级别的。
证明:对于某个点 \(u\) 分情况讨论:
- 如果 \(u\) 在原无向图中度 \(\le\sqrt{m}\),那自然在新图中出度也 \(\le\sqrt{m}\)
- 如果 \(u\) 在原无向图中度 \(>\sqrt{m}\),那它在新图中只会指向度 \(\ge deg_u>\sqrt{m}\) 的点,而这样的点个数显然 \(\le\mathcal O(\dfrac{m}{\sqrt{m}})=\mathcal O(\sqrt{m})\)
考虑通过这个有向图间接求出三元环、四元环的个数。
三元环计数
显然对于一个三元环 \((A,B,C)\),它唯一对应刚刚建出的有向图中某个满足存在 \(A\to B,B\to C,A\to C\) 边相连的三元组 \((A,B,C)\),因此考虑暴力枚举 \(A\),暴力枚举 \(A\) 的出边指向的点 \(B\),暴力枚举 \(B\) 的出边指向的点 \(C\),check 是否存在 \(A\to C\) 边即可。
时间复杂度?注意到在我们第一遍枚举 \(A\to B\) 出边时遍历了所有 \(m\) 条边,而根据之前推出的性质,第二次枚举 \(B\) 的出边最多有 \(\sqrt{m}\) 个,因此总复杂度 \(m\sqrt{m}\)。
还有一个细节是怎样判断是否存在 \(A\to C\) 边。dy 那篇 \(\mathcal O(1)\) 判断两点之间是否存在边?\(\mathcal{NONONO}\)。考虑记一个 \(tim_i\) 表示 \(i\) 上一次被更新的时间,在枚举 \(A\to B\) 之前我们先枚举一遍 \(A\) 的所有出边指向的点 \(B\) 并令 \(tim_B\leftarrow A\),那么我们枚举 \(C\) 时如果发现 \(tim_C=A\) 就说明 \(C\) 上一次是被 \(A\) 更新的,也就间接证明存在边 \(A\to C\) 了。
for(int i=1;i<=m;i++) deg[u[i]]++,deg[v[i]]++;
for(int i=1;i<=m;i++){
if(mp(deg[u[i]],u[i])>mp(deg[v[i]],v[i])) swap(u[i],v[i]);
g[u[i]].pb(v[i]);
} int ans=0;
for(int i=1;i<=n;i++){
for(int j:g[i]) tim[j]=i;
for(int j:g[i]) for(int k:g[j]) if(tim[k]==i)
ans++;
}
四元环计数
这个比三元环计数稍微复杂些,但还不算困难。
考虑一个四元环 \((A,B,C,D)\) 对应到图上有哪些可能,列举一下也无非就以下三种:
- \(A\to B,B\to C,A\to D,D\to C\)
- \(A\to B,B\to C,C\to D,A\to D\)
- \(A\to B,A\to D,C\to B,C\to D\)
考虑对三种情况一一计数,对于第一种情况我们枚举 \(A\),我们记以 \(C\) 结尾的满足存在边 \(A\to B,B\to C\) 的点 \(B\) 个数为 \(f_C\),那么这样的四元环个数即为 \(\sum\limits_{C}\dbinom{f_C}{2}\),这个在枚举 \(C\) 的过程中可以求得。
对于第二、三种情况,有一个注意点,就是对于一个点 \(A\) 而言,求满足存在 \(A\leftarrow B,B\to C\) 的点 \(B\) 个数 \(cnt_C\) 直接枚举是没问题的,但是求满足存在 \(A\to B,B\leftarrow C\) 的点 \(B\) 个数就不能直接枚举了,因为在新建的图中每个点的入度是没有任何性质的,一个菊花图就能把你卡成 \(n^2\)。
因此在第二种情况中考虑枚举 \(B\),那么就可以将四元环拆成两个基本模型 \(B\to C,C\to D\) 和 \(B\leftarrow A,A\to D\),这两部分都是可以 \(m\sqrt{m}\) 枚举的,记两部分个数分别为 \(f_D\) 和 \(g_D\),那么这样的四元环个数就是 \(\sum\limits_{D}f_Dg_D\)。
对于第三种情况考虑枚举 \(B\),那么也可以拆成两个基本模型 \(B\leftarrow C,C\to D\) 和 \(B\leftarrow A,A\to D\),这一类的贡献即为 \(\sum\limits_{D}\dbinom{g_D}{2}\),但由于 \(B,D\) 地位相同,故同一个这一类的四元环会被算两次,需除以 \(2\)。
最终四元环个数即为这三种情况贡献之和。时间复杂度还是 \(m\sqrt{m}\)。
for(int i=1;i<=m;i++) deg[u[i]]++,deg[v[i]]++;
for(int i=1;i<=m;i++){
if(mp(deg[u[i]],u[i])>mp(deg[v[i]],v[i])) swap(u[i],v[i]);
g[u[i]].pb(v[i]);rg[v[i]].pb(u[i]);
} int ans=0;
for(int i=1;i<=n;i++){
int B1=0,B2=0,B3=0;
for(int j:g[i]) for(int k:g[j]) if(k^i) (B1+=cnt1[k])%=MOD,cnt1[k]++;
for(int j:rg[i]) for(int k:g[j]) if(k^i) (B2+=cnt1[k])%=MOD,(B3+=cnt2[k])%=MOD,cnt2[k]++;
for(int j:g[i]) for(int k:g[j]) cnt1[k]=0;
for(int j:rg[i]) for(int k:g[j]) cnt2[k]=0;
ans=(0ll+ans+B1+B2+1ll*INV2*B3)%MOD;
}
例题:
1. P6815 [PA2009]Cakes
没啥好说的,直接枚举每个三元环对贡献求和即可,毕竟三元环计数是可以枚举到每个三元环的。
2. CF985G Team Players
3. Codeforces Gym 102028L Connected Subgraphs
首先考虑合法的边集长什么样,简单按度数分类讨论以下可得总共有以下五种情况:
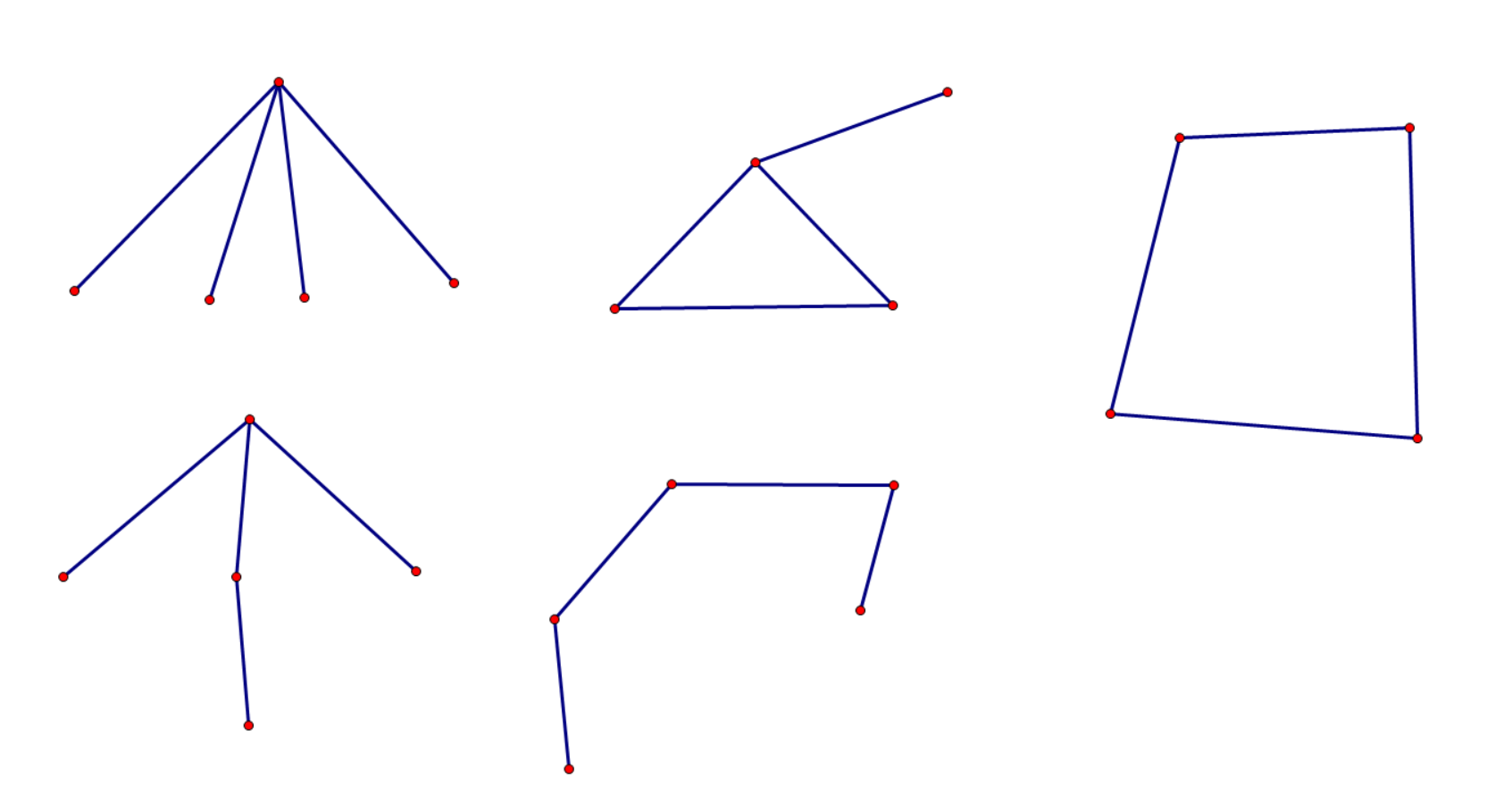
我们记从左到右、从上到下五种情况的方案数分别为 \(C_1,C_2,C_3,C_4,C_5\),那么显然 \(C_1\) 是非常好求的,就是 \(\sum\limits_{i=1}^n\dbinom{deg_i}{4}\),\(C_3\) 也非常 simple,直接枚举每个三元环 \((i,j,k)\),贡献为 \(deg_i-2+deg_j-2+deg_k-2\),\(C_5\) 就是一个四元环的板子,棘手的地方在于 \(C_2\) 和 \(C_4\)。考虑正难则反,我们考虑枚举第二幅图中度数为 \(3\) 的点 \(i\) 以及度数为 \(2\) 的点 \(j\),那么贡献就是 \((deg_j-1)\dbinom{deg_i-1}{2}\),同理在第四幅图中我们枚举中间的点 \(i\),那么贡献即为 \(\sum\limits_{(i,j),(i,k)\in E,j\ne k}(deg_j-1)(deg_k-1)\),这个前缀和扫一遍算一下即可,但是不难发现这样会算重,\(C_3\) 在计算第二副图的过程中被算了 \(2\) 次,在计算第四幅图的过程中也被算了 \(2\) 次,因此需减掉 \(3C_3\) 的贡献。\(C_5\) 在计算第四幅图的过程中被算了 \(4\) 次,需减掉 \(3C_5\)。还有,对于一个三元环 \((i,j,k)\) 而言,当我们计算 \(C_4\) 时也会把形如 \((i,j,k,i,j)\) 这样的长度为 \(4\) 的链算进去,因此还会多产生 \(3\times\text{三元环个数}\) 的贡献,因此总共重复计算的贡献就是 \(3\times(C_3+C_5+\text{三元环个数})\)
时间复杂度 \(Tm\sqrt{m}\)(所以这个 20s 时限是干嘛用的)
4. 「2017 山东一轮集训 Day6」三元组
首先看到互质,反演!即
直接枚举是三方的,一脸无法通过,因此考虑优化,注意到对于某个三元组 \(x,y,z\),只有当 \(\text{lcm}(x,y),\text{lcm}(y,z),\text{lcm}(z,x)\) 均 \(\le\max\{a,b,c\}\) 且 \(\mu(x),\mu(y),\mu(z)\) 均非零的时候才可能产生贡献,打个表即可发现 \([1,50000]\) 中满足 \(\mu(i)\ne 0\) 的数只有 \(10008\) 个,而它们当中满足 \(\text{lcm}(x,y)\le 50000\) 的整数对 \((x,y)\) 只有 \(10^5\) 级别,因此考虑求出该图的所有三元环,\(3!\) 枚举它们分别对应 \(x,y,z\) 中的哪个,这部分复杂度是 \(m\sqrt{m}\) 的。但三元环只能处理 \(x,y,z\) 两两不同的情况,对于 \(x,y,z\) 中存在重复值的情况,就分存在两个数相同和三个数都相同两种情况处理,对于两个数相同的情况就 \(\mathcal O(m)\) 枚举一遍边集然后瞎算一下贡献即可,对于三个数相同的情况就直接枚举它们是啥即可。
5. Codeforces Gym 100342J Triatrip
有向图三元环个数……好像跟这篇文章的标题不太搭(
考虑枚举其中两个点 \(A,B\),那么第三个点 \(C\) 需要满足的条件是存在 \(B\to C,C\to A\) 的边,bitset 取个并即可,这题 \(n\le 1500\) 刚好开得下 \(n\) 个长度为 \(n\) 的 bitset
然鹅这题我 WA 了 114514191981019260817998244353 发,一次是由于数组开小了开成了 \(10^3\),还有两次是忘了开 ll……我果真活回去了/cg/cg
6. P4619 [SDOI2018]旧试题
SDOI:我抄我自己(London Fog
首先考虑 \(d(ijk)\) 是个什么东西,联想到 P3327 [SDOI2015]约数个数和 中 \(d(ij)\) 的展开式 \(d(ij)=\sum\limits_{x\mid i}\sum\limits_{y\mid j}[x\perp y]\) 可得 \(d(ijk)=\sum\limits_{x\mid i}\sum\limits_{y\mid j}\sum\limits_{z\mid k}[x\perp y][y\perp z][z\perp x]\),证明可仿照那题,这里就不再赘述了。
因此我们有
其中 \(V(x)=\sum\limits_{y=1}^x\lfloor\dfrac{x}{y}\rfloor\),可以整除分块求出。
式子化到这里就和 「2017 山东一轮集训 Day6」三元组 一样了,三元环随便求求即可,唯一的一点就是卡常,卡得要死要活,大概介绍一下我的卡常方式:
- 在 \(3!\) 枚举三元环中三个点的对应方式时可以把三个 \(\mu\) 的乘积提前存下来,不必每次都乘一遍,也可以合并同类项,把 \(V(\dfrac{A}{\text{lcm}(w,u)})V(\dfrac{B}{\text{lcm}(u,v)})V(\dfrac{C}{\text{lcm}(v,w)})+V(\dfrac{A}{\text{lcm}(w,u)})V(\dfrac{C}{\text{lcm}(u,v)})V(\dfrac{B}{\text{lcm}(v,w)})\) 并成 \(V(\dfrac{A}{\text{lcm}(w,u)})(V(\dfrac{B}{\text{lcm}(u,v)})V(\dfrac{C}{\text{lcm}(v,w)})+V(\dfrac{C}{\text{lcm}(u,v)})V(\dfrac{B}{\text{lcm}(v,w)}))\),这样就只用取三次模了,常数能减小一半。
- 在建图时把每个点对的 \(\text{lcm}\) 提前预处理出,不必每次遍历都重新求一遍,同时可以用
vector存邻接表并将邻接表中元素按 \(\text{lcm}\) 从小到大排序,如果遍历到某个点发现 \(\text{lcm}>\max\{A,B,C\}\) 就直接break掉,起到剪枝的作用。
但即便加了这两个优化后我的程序加起来还是跑了 \(16.61\text{s}\),说明我是 sb!
小结
一言以蔽之,无向图三元环/四元环的题目如果把图明确给你了,那么暗示还是相当明显的,就直接求好了,但是有时候题目不会显式地将图论模型摆出来(比方说上文中的某些三元环与数论相结合的题目),这时候你就要运用你善于发现的眼睛,发现题目中隐藏的图论模型,从而将题目转化为无向图三/四元环的问题。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号