wqs二分 学习笔记
wqs二分适用情况是在 选恰好p个 的条件下,还需满足答案函数(也就是下文的 \(g(x)\) )具有凹凸性。
设 \(g(x)\) 是恰好选 \(x\) 个的答案,则最终答案就是 \(g(p)\)。而这个 \(g(x)\) 直接算很难算出来,或者说我们无法一开始就得到,但我们发现 \(g(x)\) 具有凹凸性。如果对于所有 \(x\) ,我们在平面直角坐标系上放入点 \((x,g(x))\) ,这些点构成一个凸壳,相邻之间的斜率具有单调性。
这里我们先讨论是凸函数的情况(及函数图像为一个上凸壳)。
我们任取一个斜率的直线进行平移直到与这个凸壳相切。设它与凸壳切在了 \(x=t\)。当 \(t<p\) 时我们就将 \(t\) 变小;当\(t>p\) 时我们就将 \(t\) 变大,直到 \(t=p\) 为止。
(图片来源于Leap_Frog的洛谷日报)
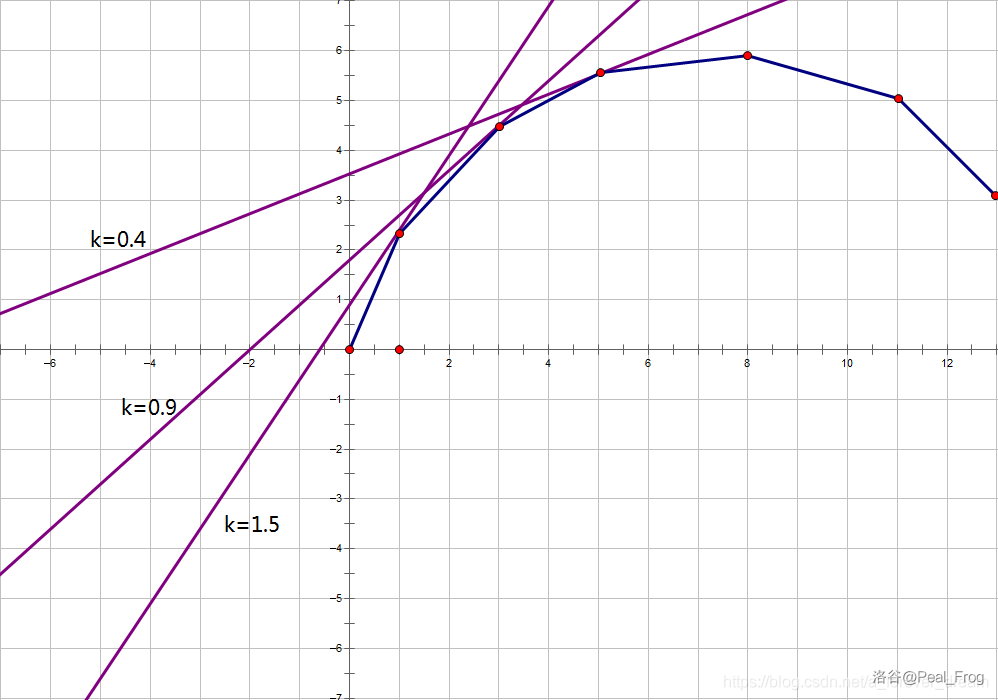
不是说我们不知道 \(g(x)\) 吗?那我们怎么求切点在哪啊?
设这条直线斜率为 \(k\)。此时我们不断去上下平移这条直线。对于点 \((x,g(x))\) ,设该直线经过它时表达式为 \(y=kx+b\),而对于不同的 \(x\),这个 \(b\) 是不同的。
其实切点即是 \(b\) 值最大的那个 \(x\)。
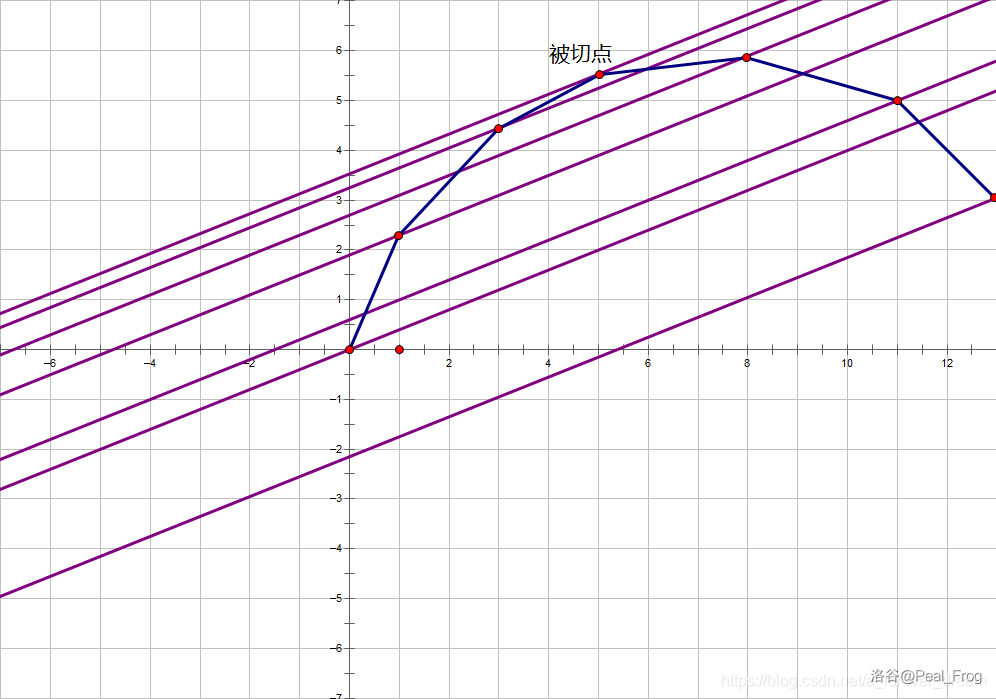
所以我们设 \(f(x)\) 为经过 \((x,g(x))\) 时的 \(b\) 值。
所以有 \(g(x)=kx+f(x)\)。现在问题是如何求这个 \(f(x)\) 了。有 \(f(x)=g(x)-kx\)。所以 \(f(x)\) 是很好求的,我们只用将每一个被要求选 恰好p个的物品的代价减去 \(k\)。这样再贪心求出最大值答案(不一定是简单的找最大值,还可能是最大生成树,dp求最大值等,详见后面例题)。那么对应的最大值 \(f(x)\) 的 \(x\) 就是 \(t\) 的值。判断完后将物品的代价恢复为原来的值,被减去 \(k\) 的要加回来。
那么最后二分完我们会得到一个斜率 \(k\)。然后再代入该斜率如上求出 \(f(p)\) 即可。最后还要将答案加上 \(k\times p\) 就得到 \(g(p)\)。
有些时候这个斜率会减成负的,所以视具体情况定二分上下界。
那么当答案函数为凹函数时,其实情况也差不多。只不过在 \(t<p\) 时应该让 \(k\) 变大;\(t>p\) 时让 \(k\) 变小。并且每取一个 \(-k\) 要改成每取一个 \(+k\)。
很多时候不一定要严格证明出凹凸性。可以猜结论打表找规律。
还要注意,有可能出现一条直线与凸壳相切在多个点上,这个时候可以手动去规定是取最左点还是最右点。
例题1 P2619 [国家集训队] Tree I
这道题有 恰好选p个 的条件,而根据打表和感性理解,答案函数应该是一个凹函数。
分开记录黑边和白边,分别提前按边权从小到大排好序,方便后面归并排序。那么二分答案斜率 \(k\)。将所有白边的权值减去 \(k\),再用归并排序的顺序用Kruskal加边跑最小生成树,则 \(t\) 为该生成树中白边数量。别忘了判断完把白边的权值改回来。
若 \(t<p\) 应该让 \(k\) 变大;\(t>p\) 时让 \(k\) 变小。
最终找到这个 \(k\) 再代入求出边权和,再加上 \(need\times k\) 就是答案。时间复杂度 \(O(n\alpha(n)\log V)\),\(\alpha(n)\) 为并查集时间复杂度。
因为斜率可能为负,二分上下界为 \([-100,100]\),因为边权 \(\le 100\)。
为什么可能为负呢?如果正常跑最小生成树,而得到的生成树中有 \(d\) 条白边,则在 \([0,d]\) 的范围内斜率为负。
代码:
#include<bits/stdc++.h>
#include<cstring>
using namespace std;
const int N=2e5+5;
int n,m,need,wt,bk,fa[N];
struct edge
{
int v,u,w;
bool operator<(const edge &a)
{
return w<a.w;
}
}bl[N<<1],wh[N<<1];
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int find(int x)
{
if(fa[x]!=x)fa[x]=find(fa[x]);
return fa[x];
}
bool unionn(int x,int y)
{
int xx=find(x),yy=find(y);
if(xx==yy) return 0;
fa[xx]=yy;
return 1;
}
bool check(int k)
{
for(int i=1;i<=n;i++) fa[i]=i;
int pl=1,pr=1,num=0;
while(pl<=wt&&pr<=bk)
{
if(wh[pl].w+k<=bl[pr].w) num+=unionn(wh[pl].u,wh[pl].v),pl++;
else unionn(bl[pr].u,bl[pr].v),pr++;
}
while(pl<=wt) num+=unionn(wh[pl].u,wh[pl].v),pl++;
return num<need;
}
int main()
{
n=read(),m=read(),need=read();
for(int i=1;i<=m;i++)
{
int u=read()+1,v=read()+1,w=read(),col=read();
if(!col) wh[++wt].u=u,wh[wt].v=v,wh[wt].w=w;
else bl[++bk].u=u,bl[bk].v=v,bl[bk].w=w;
}
sort(bl+1,bl+bk+1);
sort(wh+1,wh+wt+1);
wh[wt+1].w=1e9;
bl[bk+1].w=1e9;
int l=-100,r=100,ans=-100;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1;
else ans=mid,l=mid+1;
}
int sum=0;
for(int i=1;i<=n;i++) fa[i]=i;
int pl=1,pr=1;
while(pl<=wt&&pr<=bk)
{
if(wh[pl].w+ans<=bl[pr].w) sum+=(wh[pl].w+ans)*unionn(wh[pl].u,wh[pl].v),pl++;
else sum+=bl[pr].w*unionn(bl[pr].u,bl[pr].v),pr++;
}
while(pl<=wt) sum+=(wh[pl].w+ans)*unionn(wh[pl].u,wh[pl].v),pl++;
while(pr<=bk) sum+=bl[pr].w*unionn(bl[pr].u,bl[pr].v),pr++;
printf("%d\n",sum-ans*need);
return 0;
}
P5633 最小度限制生成树 跟他是双倍经验,在此不再赘述。
例题2 P5308 [COCI 2018/2019 #4] Akvizna
题目出现了 恰好k轮胜利 的字眼。可能可以用wqs二分,还需进一步探索凹凸性。
发现正着考虑太难了,所以考虑从后往前 \(dp\)。设 \(dp_i\) 为剩下 \(i\) 个选手最大的奖金。
则有转移:
然后感性理解 and 打表发现这 \(dp\) 函数是一个上凸函数。(因为不会严谨证明)
那么就可以用wqs二分去做了。二分斜率 \(k\),那么在这题当中就是每赢一场的奖金要减去 \(k\)。
也就是转移变成了这个样子:
同时,为了得到切点的横坐标,我们还需记录 \(num_i\) 表示 \(dp_i\) 最大值需要经过多少次转移(也就是赢多少场)。那么 \(num_n\) 就是切点横坐标。
那么二分解决了,但是这个时间复杂度是 \(O(n^2\log V)\)。别说 \(10^5\) 了,连 \(5000\) 都过不了。
发现其实最慢的是跑 \(dp\) 的过程。简化一下式子:
然后发现中间有一项 \(\frac{j}{i}\) 跟 \(i,j\) 都有关系。考虑斜率优化。再转化一下式子:
然后斜率是 \(j\)。发现 \(-\frac{1}{i}\) 单增,\(j\) 单增,直接单调队列维护上凸壳,优化成 \(O(n)\)。
最终时间复杂度 \(O(n\log V)\)。本题有点卡精度,实测要开到 \(10^{-13}\) 才能卡过。或者说用交叉相乘?
会发现二分上界是 \(1\) ,下界是 \(0\)。因为单场奖金最大是 \(1\)。
代码:
#include<bits/stdc++.h>
#include<cstring>
using namespace std;
const int N=2e5+5;
const double eps=1e-13;
int n,q[N],num[N],k;
double dp[N];
struct line
{
double k,b;
}l[N];
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
double inter(int i,int j)
{
return 1.0*(l[j].b-l[i].b)/(l[i].k-l[j].k);
}
bool check(double mid)
{
int hd=1,tl=1;
for(int i=1;i<=n;i++)
{
while(hd<tl&&inter(q[hd],q[hd+1])+1.0/i<eps) hd++;
int j=q[hd];
dp[i]=dp[j]+1-mid-1.0*j/i;
num[i]=num[j]+1;
l[i].k=i,l[i].b=dp[i];
while(hd<tl&&inter(i,q[tl])-inter(i,q[tl-1])<eps) tl--;
q[++tl]=i;
}
return num[n]<k;
}
int main()
{
n=read(),k=read();
double L=0,R=1,ans=0;
while(eps<R-L)
{
double mid=(L+R)/2;
if(check(mid)) R=mid-eps;
else ans=mid,L=mid+eps;
}
int hd=1,tl=1;
for(int i=1;i<=n;i++)
{
while(hd<tl&&inter(q[hd],q[hd+1])+1.0/i<eps) hd++;
int j=q[hd];
dp[i]=dp[j]+1-ans-1.0*j/i;
l[i].k=i,l[i].b=dp[i];
while(hd<tl&&inter(i,q[tl])-inter(i,q[tl-1])<eps) tl--;
q[++tl]=i;
}
printf("%.9f",dp[n]+ans*k);
return 0;
}
P4983 忘情 做法差不多,也是 wqs二分+斜率优化 。
例题3 P1484 种树
发现这个题条件变成 至多k个 了而不是 恰好k个了,这咋整?
先别慌,看一看有没有凹凸性。根据打表+猜结论+感性理解可知应该是一个上凸壳。而上凸壳一定有 \(y\) 坐标最高的点(如有多个,任取其一),设其横坐标为 \(d\)。则当 \(d\le k\) 时是不是可以直接取 \(g(d)\) 了。所以代入斜率为 \(0\) 即可得到 \(g(d)\)。
现在考虑当 \(d>k\),则 \(g(x)\) 在 \([0,k]\) 上非降。所以直接取 \(g(k)\) 是最大的。所以wqs二分求 \(g(k)\) 即可。
#include<bits/stdc++.h>
#include<cstring>
using namespace std;
const int N=1e6+5;
#define int long long
int n,a[N],dp[N][2],m,num[N][2];
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int calc(int k)
{
for(int i=1;i<=n;i++)
{
dp[i][1]=dp[i-1][0]+a[i]-k;
num[i][1]=num[i-1][0]+1;
if(dp[i-1][1]>dp[i-1][0]) num[i][0]=num[i-1][1];
else num[i][0]=num[i-1][0];
dp[i][0]=max(dp[i-1][0],dp[i-1][1]);
}
if(dp[n][0]>dp[n][1]) return num[n][0];
return num[n][1];
}
signed main()
{
n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=read();
if(calc(0)<=m)
{
printf("%lld\n",max(dp[n][0],dp[n][1]));
return 0;
}
int l=-1e6,r=1e6,ans=0;
while(l<=r)
{
int mid=(l+r)>>1;
if(calc(mid)<=m) ans=mid,r=mid-1;
else l=mid+1;
}
calc(ans);
printf("%lld\n",max(dp[n][0],dp[n][1])+m*ans);
return 0;
}
练习题:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号