2025.01 做题记录
难度评级 \(x\):
\(x\in[0,1]\): 自己切了(记思考过程)
\(x\in(1,2]\): 有思路,看题解懂了(记自己思路与正解)
\(x\in(2,3]\): 完全没思路(记正解)
1. AT_agc005_d ~K Perm Counting
难度:1.2
首先看到这种排列 \(p_i\) ,答案与 \(|p_i-i|\) 的要么是构造一个长为 \(2n\) 的数组满足 \(\forall i\in[1,n]\) 都在数组里出现恰好两次,然后匹配;或者说转化为二位平面上横坐标与纵坐标的匹配。
本题考虑后者,构建二维数组。
设 \(n=7,k=2\)。
(图出自@Dreamunk的题解)
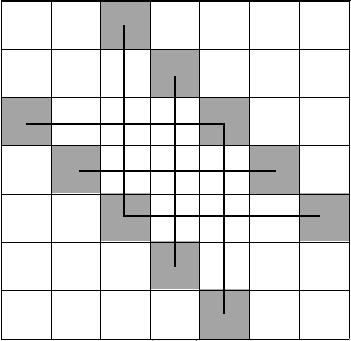
则以上所有灰色格子不能取,因为 \(|i-j|=k\)。所以问题转化为在棋盘上选出 \(n\) 个白色格子使得任意一行任意一列有且仅有一个格子被选。
然后考虑容斥,我们拿总方案 减去 取了至少 \(1\) 个灰格子的方案 加上 取了至少 \(2\) 个灰格子的方案......
但是会发现有些灰格子不能同时取,如果一行或一列有多个灰格子,则不能同时取这些格子。那么我们把所有不能同时取得格子连一条边,则最终这个图会是若干条链组成。然后跑dp求独立集方案再合并起来就是方案了。
但是除去我们既定的灰格子,我们还要选其它白格子,这里就用没被选的列去匹配没被选的行。设选了 \(i\) 个灰格子,则剩下的格子选的方案为 \((n-i)!\)。
则答案为 \(\sum_{i=0}^{n}(-1)^idp_i(n-i)!\)。
时间复杂度 \(O(n^2)\)。
2. P3160 [CQOI2012] 局部极小值
难度:2
首先发现 X 最多只有 \(8\) 个。而且当两个 X 相邻时是无解的。
考虑从小到大填入每一个数,会发现局部极小值必须比非局部最小值先填。
设 \(dp_{i,S}\) 表示填入 \(1\sim i\) 后已经被填的局部最小值状态为 \(S\) 的方案数。我们可以将所有局部最小值编号,然后就可以用二进制数表示了。
那么填数时分两种情况:
-
填入非局部最小值。
我们需要求出有多少个非局部最小值可以填,设 \(ab_S\) 为已填局部最小值状态为 \(S\) 的情况下可以填的非局部最小值。
因为与没被填的局部最小值相邻的位置是不能填的,所以可以枚举所有状态然后直接预处理出来。
还要剔除之前已经填进去的数,则有 \(\max(0,ab_S-i+1-S二进制下1的个数)\)。为了方便,我们让 \(ab_S\gets ab_S+S二进制下1的个数\)。则有转移:
\[dp_{i,S}=dp_{i-1,S}\times \max(0,ab_S-i+1) \] -
填入局部最小值
则枚举没被填的局部最小值 \(j\),则有转移:
\[dp_{i,S|2^{j-1}}=\sum_{j\notin S}dp_{i-1,S} \]
初始化 \(dp_{0,0}=1\),答案为 \(dp_{nm,2^{cnt}-1}\),\(cnt\) 为局部最小值的个数。
但是这样不对,因为我们在任意地填非局部最小值时可能会导致某些 非局部最小值 变成了 局部最小值,不符合题意。
也就是说我们求的是至少有 \(cnt\) 个局部最小值且这 \(cnt\) 个局部最小值就是要求的。
所以我们要用容斥去去掉这一部分不合法的情况。
设要求的局部最小值有 \(cnt\) 个,那么答案为 \(至少有这cnt个局部最小值的答案-至少有这cnt+1个局部最小值的答案+至少有这cnt+2个局部最小值的答案...\)
然后因为最多有 \(8\) 个局部最小值,所以可以暴力一下发现最多选局部最小值的方案小于 \(2\times 10^4\)。那么对于每一种情况我们都对它进行如上的dp,则时间复杂度为 \(O(nmw2^{cnt})\),其中 \(w\le 2\times 10^4\) ,为选局部最小值的方案,\(cnt\le 8\)。所以总的计算次数 \(\approx 6\times 10^7\) 左右。
所以直接搜索,把能选成局部最小值的非局部最小值 选或不选,这里也需满足任意两个局部最小值不相邻。我们再带一个参数 \(f=1或-1\),然后每多选一个局部最小值就让 \(f\gets -f\),则答案为 \(\sum f\times dp_{nm,2^{cnt}-1}\)。
3. AT_agc040_c Neither AB nor BA
难度:2.1
妙妙题,真的妙啊。
我们发现,如果想要删一对数 \(\{a_i,a_j\},i<j\),能删当且仅当 \(i,j\) 奇偶性不同。而我们又不能删 AB 和BA,所以考虑将所有奇数位的所有 B 变成 A,所有A 变成 B,这样条件就变成不能删 AA 和 BB 了。
正难则反,考虑用所有串减去不合法串。一共有 \(3^n\) 个串。
那么发现,如果此时 A 不能删完当且仅当 \(A的个数\ge \lfloor\frac{n}{2}\rfloor+1\),B 同理。
所以我们枚举 A 的个数 \(i\),则先要选出 \(i\) 个 A ,方案数为 \(n\choose i\),剩下的位置随便填 B或 C,方案数为 \(2^{n-i}\)。然后发现 B 不能被删完也同理,所以答案为:
直接处理出来,时间复杂度 \(O(n\log n)\),虽然是 \(n\le 10^7\),但是 4s。
4. P6846 [CEOI2019] Amusement Park
难度:3
一眼状压好吧。
我们发现,如果我们能够通过更改 \(x\) 条边使得该图变为一个DAG,那么我们也可以通过更改 \(m-x\) 条边使得该图变为另一个DAG,并且这个DAG每一条边都是另一个DAG的反向边。
所以让我们求所有方案的更改边数 实际上可以转化为求 \(选边方案数\times \frac{m}{2}\)。因为上述两种情况都会计入方案数,而他们的更改边数和为 \(m\)。
然后就是求方案数了,设 \(dp_S\) 表示已经状态 $ S $ 构成DAG的方案数。
因为不用考虑方案具体是什么,所以考虑不断加入在目前图中还未加入的点作为同一层,而这些集合必须是一个独立集,也就是集合内任意两点无连边。如果不是独立集就不能作为同一层加入。
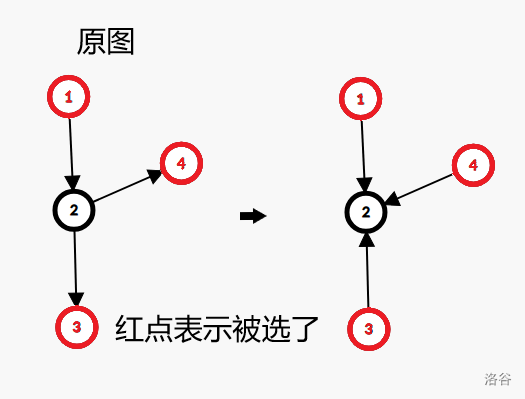
所以只要选的点是独立集就一定可以把它继续变成一个DAG。
所以我们先把所有是独立集的状态集合预处理出来。但是会发现会重复统计,比如说原本同一层的点可以分成几次加入,也可以一次加入。所以方案为一个一个加入 减去 两个两个加入的方案数 加上 三个三个加入的方案数...
所以设 \(T\) 为加入的点集,则容斥系数为 \((-1)^{|T|+1}\)。
综上,转移为:
枚举子集时间复杂度 \(O(3^n)\)。
初始化 \(dp_0=1\),答案为 \(dp_{2^n-1}\times \frac{m}{2}\)。
时间复杂度 \(O(3^n+m2^n)\)。
5. AT_agc039_c Division by Two with Something
难度:2.2
6. CF1208F Bits And Pieces
难度:2
首先是贪心从大到小每一位考虑,如果能取 \(1\) 就取 \(1\),否则就取 \(0\)。
怎么判断是否能取 \(1\) 呢?
设当前需要判断是否能取的状态为 \(x\),则我们需要去枚举状态 \(y\) 满足 \(y\in x\),找到 \(a_j,a_k,j<k\) 满足二进制下 \(y\in a_j,y\in a_k\)。找到 \(a_i\) 满足 \((x\ \text{xor}\ y)\in a_i\),并且 \(i<j\)。
那么有这个子集的操作,所以考虑用高维前缀和求超集。我们处理出 \(x\in a_j\) 最大的两个 \(j2,j3\),和最小的 \(j1\)。然后判断一个状态是否能取就枚举它的子集,判断对应的 \(j1\) 是否小于 \(j2\)。
时间复杂度 \(O(n\log V)\)。
7. P2257 YY的GCD
难度:3
钦定 \(n<m\)。
求:
首先我们知道 \(\sum_{d|n}\mu(d)=[n=1]\),代入 \(n=\gcd(i,j)\),则有 \(\sum_{d|\gcd(i,j)}\mu(d)=[\gcd(i,j)=1]\)。
所以先转化成能带入的式子,则有:
再代入,有:
虽然感觉已经很优秀了,但是还是无法通过。
设 \(T=kd\),则有:
而后者可以预处理。用线性筛求出质数及莫比乌斯函数,然后枚举每个质数的倍数,再用前缀和处理一下即可。时间复杂度远小于 \(O(n\ln n)\),可能接近 \(O(n)\)。
然后对于每一次询问,用数论分块去做前面的部分,再结合前缀和求出答案。
时间复杂度 \(O(n+q\sqrt n)\)。
8. P3312 [SDOI2014] 数表
难度:0.5
设 \(f_i\) 为 \(\sum_{d|i,d\in\mathbb{N^+}} d\),也即所有能整除 \(i\) 的正整数之和。
先不考虑 \(\le a\) 的限制并钦定 \(n\le m\),则根据题目,列出式子,则答案为:
后面那坨,直接代入莫比乌斯反演公式,则有:
设 \(T=kd\),则有:
\(f\) 和后面的 \(\sum\) 可以预处理出来,时间复杂度是调和级数,约为 \(O(n\ln n)\)。再求一下前缀和方便后面使用。
然后对于前面的部分可以用数论分块,时间复杂度 \(O(\sqrt n)\)。
但是有一个问题,我们还有 \(f(i)\le a\) 的限制,这个怎么做?
会发现,当 \(a<f(i)\) 时,我们可以让 \(f(i)=0\),而当 \(a\ge f(i)\) 时,我们就正常计算。
所以将所有询问离线下来并按 \(a\) 值从小到大排序,这样每一次查询时,将所有 \(a_{j-1}<f(i)\le a_j\) 的所有 \(f(i)\) 的值算出来并更新前缀和,再正常用数论分块处理即可。
发现前缀和需要动态维护,所以用树状数组维护。而每一个 \(f(i)\) 最多被计算一次,所以时间复杂度是正确的。
时间复杂度 \(O(n\ln n\log n+q\sqrt n\log n)\)。而 \(q\le 2\times 10^4\),可以通过。
9. P4331 [BalticOI 2004] Sequence 数字序列
难度:2
首先发现递增序列有点难搞,所以考虑 \(a'_i=a_i-i\),\(b'_i=b_i-i\)。因为有 \(\sum_{i=1}^n|a_i-b_i|=\sum_{i=1}^{n}|a'_i+i-b'_i-i|=\sum_{i=1}^n|a'_i-b'_i|\),所以问题转化为求单调不降的序列 \(b'\) 即可。
那么就可以让一段连续 \(b'_i\) 相等。因为对于一些数 \(c_i\),则使得 \(\sum_{i=1}^n|c_i-x|\) 最小的 \(x\) 是\(c_i\) 的中位数,所以有可能我会将一段的 \(b'_i\) 全部赋值为该段的中位数。
首先如果去掉 \(b'\) 单调不降的限制,则最优答案为 \(b'_i=a'_i\),但是有单调不降的限制,所以需要合并成一段,并让该段的所有 \(b'_i\) 为这一段数的中位数之值。
我们先把每一个数看成一段,如果这一段的中位数小于上一段的中位数,那么就不合法,所以只能将这一段与上一段进行合并,再求中位数。
因为每一次只会将不合法的位置合并起来,所以最后求出来的是合法情况中最优情况。
开一个栈存下当前仍存在的段。我们先把每一个数看成一段,然后不断往前合并,直到栈顶的段的中位数大于等于它上一个段的中位数。
那么怎么快速求一个段的中位数并支持合并?
想到用左偏树去解决。我们直接将该段中大于中位数的所有数全部弹出,每一次合并后都这样做,这样堆顶就是中位数。
为什么不怕把可能的中位数给删去呢?因为该段只会在后一段的中位数小于它的中位数时才合并,而合并完该段的中位数一定不大于原来该段的中位数,所以可以直接删。
这样就做完了,最后输出 \(b_i=b'_i+i\) 即可。
最多会通过 \(n-1\) 次合并将所有数合并到一个段内,时间复杂度 \(O(n\log n)\)。
10. P5278 算术天才⑨与等差数列
难度:2
如何判断一个区间从小到大排序能形成一个公差为 \(k\) 的等差序列?
首先,如果 \(\max_{i=l}^ra_i\neq (r-l)\times k+\min_{i=l}^r a_i\) 则一定无解。
然后发现该区间的值 \(\% k\) 都相等,所以任意两数差
一定 \(k\) 的倍数。所以只用判断相邻两数的差是否是 \(k\) 的倍数即可,需要维护区间相邻两数差的 \(\gcd\),判断它们的 \(\gcd\) 是否是 \(k\) 的倍数。
但是,差都是 \(k\) 的倍数仅仅是公差为 \(k\) 等差序列的必要不充分条件。因为可以当 \(k=2\),\(a=\{1,5,5,7\}\),就不对。所以还需补上条件:区间内任意两数不相等。
判断不相等就记录 \(pre_i\) 为上一个与 \(a_i\) 相等的位置。所以当 \(\max_{i=l}^r pre_i\ge l\) 时就有重复的数。所以还要维护区间的 \(\max pre\) 值。
因为要支持单点修改,修改时 \(pre\) 值也会跟着修改。所以考虑对每一种 \(a_i\) 开一个 multiset ,维护一下即可。维护最大值最小值 \(\gcd\) 和 \(\max pre\) 就用线段树,改完后在线段树上也进行更改。
时间复杂度 \(O(n\log n+q\log n)\),常数较大。
11. P4036 [JSOI2008] 火星人
难度:1
要支持修改和插入,应该用平衡树维护。
查询操作,考虑二分LCP长度,然后判断子串是否相等即可。判断是否相等用哈希。
所以用平衡树维护哈希,支持单点修改和插入。
时间复杂度 \(O(n\log n+q\log^2n)\)。
12. P3215 [HNOI2011] 括号修复 / [JSOI2011] 括号序列
难度:2
首先思考查询,对于一个括号串,我们把所有匹配的左右括号都删去,这样剩下的串形如 ))))((((,是由若干个右括号和若干个左括号连接而成。
所以我们将 ) 替换成 \(1\),把 ( 替换成 \(-1\)。这样我们求这个剩下右括号个数就是前缀最大值,剩下左括号个数就是后缀最小值的相反数。(都与 \(0\) 取 \(\max\))
所以维护 \(\text{premax},\text{sufmin}\) 表示前缀最大值和后缀最小值。
现在考虑操作。
对于区间翻转操作,会发现 \(\text{premax}\leftrightharpoons \text{sufmax},\text{premin}\leftrightharpoons \text{sufmin}\)。所以还需要维护 \(\text{premin},\text{sufmax}\)。
对于区间取反操作,实际上就是
对于区间覆盖就直接分类讨论即可。
因为有区间翻转操作,所以用平衡树维护。时间复杂度 \(O(n\log n)\)。
13. P6105 [Ynoi2010] y-fast trie
难度:2
首先对于 \(x\ge C\),让 \(x\gets x\bmod C\)。
现在 \(x+y\in[0,2C)\),钦定 \(x\le y\)。然后分类讨论。
-
当 \(x+y\in[C,2C)\)
那么贡献就是 \(x+y-C\),所以直接找最大和次大值作为 \(y\) 和 \(x\) 即可。可以用
multiset维护。 -
当 \(x+y \in[0,C)\)
会发现情况很复杂,所以再分类讨论。
-
当 \(x,y \in[0,\frac{C}{2})\)
此时 \(x+y\) 一定满足要求,所以维护 \([0,\frac{C}{2}]\) 的最大值和次大值即可。
-
当 \(x,y \in[\frac{C}{2},C)\)
此时一定不满足要求,直接舍去。
-
当 \(x\in[0,\frac{C}{2}),y\in[\frac{C}{2},C)\)
此时有 \(x+y<C\),即 \(x<C-y\),然后找到满足要求的最小的 \(C-y\) 和最大的 \(x\)。然后可以考虑值域线段树,分别以 \(x\) 和 \(C-y\) 为下标存入 \(x\) 和 \(C-y\),然后合并时更新答案。
但是值域很大,难以开下这么大的空间。又因为强制在线,所以无法进行离散化。所以用平衡树维护即可。
-
每一次加入删除在两个 multiset 和平衡树上分别修改即可。
时间复杂度 \(O(n\log n)\)。
14. P6617 查找 Search
难度:2
设 \(pre_i\) 为最大的 \(j\) 满足 \(a_i+a_i=w\)。然后查询就判断 \(\max_{i=l}^r pre_i \ge l\) 即可。
现在需要支持修改。
会发现,对于一个位置 \(i\),\(pre_j=i\) 的 \(j\) 可能有很多个,在 \(O(n)\) 级别,如果每一次进行一次修改,那么时间复杂度为 \(O(nq\log n)\) 或 \(O(nq)\),无法通过。
但是对于 \(i\),存在 \(i<l<r\) 满足 \(a_l+a_i=a_r+a_i=w\),然后发现 \(r\) 没什么用,因为当 \(r\) 满足要求时, \(l\) 一定满足要求。
这样我们就可以建立唯一的双射 \((i,l)\)。修改时更新的 \(pre\) 值就在 \(O(1)\) 量级。
现在要将 \(a_l\gets r\),那么有哪些数的 \(pre\) 值可能被修改呢?
- 修改前 \(l\) 后面第一个与它相同的数。可能与 \(pre_l\) 建立双射。
- 修改前 \(l\) 后面第一个与它和为 \(w\) 的数。可能更改/撤销双射。
- 修改后 \(l\) 后面第一个与它相同的数。可能更改/撤销双射。
- 修改后 \(l\) 后面第一个与它和为 \(w\) 的数。可能与 \(l\) 建立双射。
- 修改后 \(l\) 自己。可能建立新的双射。
然后将这五个位置的 \(pre\) 值更改后,再在线段树上修改即可。
然后判断双射 \((i,j)\) 是否合法就判断 \(j\) 是否是 \(i\) 后第一个与 \(a_i\) 和为 \(w\) 的位置,以及 \(i\) 是否是 \(j\) 前第一个与 \(a_j\) 和为 \(w\) 的位置。用 set 维护。
时间复杂度 \(O(n\log n+q\log n)\)。
15. P11531 [THUPC2025 初赛] 检查站
难度:1
我考场上图都建出来了啊,而且也建对了啊,为什么不让我过。因为一些奇怪原因导致TLE。
想了想其它做法,感觉不太行。可能只有网络流中的最小割可以做。
现在就相当于割掉每个部门使得 \(1\) 和 \(n\) 不连通。那么割点需要拆点为边再割。
所以我们建点 \(i\) 表示原图中每一个点。 \(n+i\) 表示第 \(i\) 个部门的入点, \(n+c+i\) 为第 \(i\) 个部门的出点。
这样我们需要割掉一个部门就割掉它的出入点之间的边
。所以连边 \((n+i,n+c+i,1)\)。
但是我们还需要使得割掉这条边后它部门的所有边都断开。
对于 \(v=p_i\) 的点来说,它的到达点一定是部门入点,即 \(n+i\),且这条边不可被割掉,所以边权为 \(\text{inf}\)。但是如何连接它的出发点?因为这个出发点不受其它部门影响,所以应该直接连点 \(u\)。所以原边为 \((u,v,w)\) 的边满足 \(v=p_w\),我们应该连 \((u,n+w,\text{inf})\)。
同理,对于原边为 \((u,v,w)\) 的边满足 \(u=p_w\),我们应该连 \((n+c+w,v,\text{inf})\)。
但是你会发现,如果有边部门在 \(u\),但又有边连接了 \(u\) 但部门不在 \(u\),我们目前建出的图上来说这两条边是不连通的,所以不合法。
为了解决这个问题,我们还有对每一个部门与它所在地进行连边,这条边不可被割掉。即 \((p_i,n+i,\text{inf})\) 和 \((n+i+c,p_i,\text{inf})\)。这样就对了。
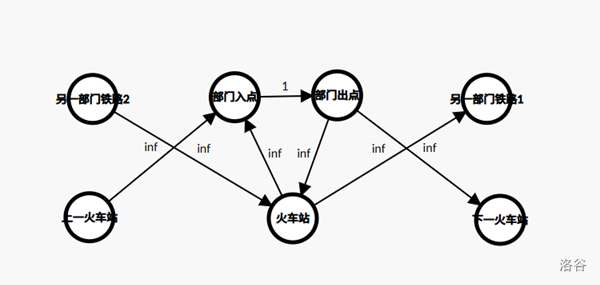
再对该图跑最小割即可。
时间复杂度我也不知道是个啥。
16. CF2048G Kevin and Matrices
难度:3
首先假设最终左边的值为 \(a_{i,j}\),右边的值为 \(a_{k,p}\)。
根据定义,有 \(a_{i,j}\ge a_{i,p}\ge a_{k,p}\)。而又要 \(a_{i,j}\le a_{k,p}\)。所以只能 \(a_{i,j}=a_{k,p}\)。
现在我们设 \(a_{i,j}=x\)。我们去枚举这个 \(x\)。
根据式子,那么我们现在需要满足:
- 任意行最大值 \(\ge x\) 。(根据不等式左边式子)
- 任意列最小值 \(\le x\) 。(根据不等式右边式子)
所以考虑设 \(f(x,y)\) 表示任意行存在 \(\ge x\) 的数,任意列存在 \(\le y\) 的数的情况。
那么我们想让上述两个条件都满足,根据容斥,则答案方案数为 \(f(x,x)-f(x,x-1)-f(x+1,x)+f(x+1,x-1)\)。
那么此时问题就在于如何求 \(f(x,y)\) 了。
发现 \(m\) 很大,而每一列的条件是一样的,所以只考虑第一列,后面每一列的方案数与第一列一样。
我们先针对第一个条件。正难则反,枚举至少有 \(i\) 行最大值 \(<x\),则剩下的行随便选。则有方案数 \((x-1)^iv^{n-i}\)。但是我们想满足条件二,要减去不合法的情况。因为只考虑这一列,所以只需让这一列所有数都 \(>y\) 即可,所以有 \(\max(x-y-1,0)^i(v-y)^{n-i}\)。
因为有 \(m\) 列,所以最后一项的指数是 \(m\)
根据二项式反演,恰好有 \(0\) 行有最大值 \(<x\) 的方案数应为
其实也就是 \(f(x,y)\) 的值。我们可以在 \(O(n(\log n+\log m))=O(n\log nm)\) 的时间求出。
别忘了我们枚举了 \(x\)。所以总时间复杂度 \(O(\sum nv\log nm)\)。
17. P5354 [Ynoi2017] 由乃的 OJ
难度:1.5
首先考虑如果是序列上的该怎么做。
可以按位考虑。对应这一位,如果输入的是 \(1\) ,在经过一段区间的计算后一定可以得到一个 \(0/1\) 值,\(0\) 也同理。设输入 \(0\) 得到了 \(w_0\),输入 \(1\) 得到了 \(w_1\)。
那么发现当 \(w_0\ge w_1\) 时,我们这一位就取 \(0\),否则如果能取 \(1\) 则取 \(1\)。
那么如何求一段区间每一位填入 \(0/1\) 后得到的结果值呢?
我们设 \(num_{i,l,r,0/1}\) 表示在区间 \([l,r]\) 中第 \(i\) 位填入 \(0/1\) 后得到的值。因为要支持修改,所以用线段树维护。将状态 \(num_{i,l,r,0/1}\to num_{i,0/1}\)。
我们记 \(rt_{i,0/1}\) 为两儿子的父亲的 \(num\) 值, \(l_{i,0/1}\) 为左儿子的 \(num\) 值, \(r_{i,0/1}\) 为右儿子的 \(num\) 值。
现在考虑合并两个区间,则有
然后把这东西用树剖转移到树上。时间复杂度 \(O(n\log^2n \log V)\)。但是万恶的 lxl 把它卡了。
那么现在需要优化掉一个 \(\log\)。可以考虑把树剖线段树改为LCT,然后就少一个 \(\log\) ,但是跑得很慢,可能会被 lxl 的 250ms 时限卡掉,主要是我不会LCT。
现在只能从合并的 \(\log V\) 下手了。
会发现 \(num_{i,0/1}\) 是一个 \(0/1\) 变量,而 \(i\le 64\),所以考虑把它压成一个 unsigned long long 值。
那么如何转移呢?只能用位运算了。
首先让 \(rt_0=l_0,rt_1=l_1\), 也就是让根节点继承左儿子的值,然后进行合并。
首先考虑 \(rt_0\)。
-
对于这里面值为 \(1\) 的位,我们要让它的值变为 \(r_1\) 的对应位,然后发现当且仅当两者这一位都是 \(1\) 时结果才是 \(1\)。所以有 \(rt_0\ \&\ r_1\)。
-
对于这里面值为 \(0\) 的位,我们要让它的值变为 \(r_0\) 的对应位。发现当 \(r_0\) 这一位是 \(1\) 且 \(rt_0\) 这一位是 \(0\) 时结果才为 \(1\)。所以先为 \(rt_0 \ |\ r_0\)。但是当 \(rt_0\) 为 \(1\) 时不满足要求,所以再 \(\oplus\ rt_0\)。
所以为 \((rt_0\ |\ r_0)\oplus\ rt_0\)。
综上,转移为 \(rt_0=(rt_0\&\ r_1)\ |\ [(rt_0\ |\ r_0)\oplus\ rt_0]\)。
同理 \(rt_1=(rt_1\&\ r_1)\ |\ [(rt_1\ |\ r_0)\oplus\ rt_1]\)。
这样就可以 \(O(1)\) 合并了。
现在还有一个问题,就是查询时走边是有顺序的,而当起点往上跳时,这个顺序刚好跟线段树中该链的顺序相反。所以除了以上信息,我们还要维护一个相反值,也就是从后往前遍历这个区间得到的答案。
那么如果称刚才的合并为左儿子合并右儿子,那么这个相反值的合并就是右儿子合并左儿子。
这样在从起点往上跳时,我们就拿链的相反值为答案。
同时记录 \(l\) 为从起点 \(u\) 跳到目前的 \(u\) 的答案,
\(r\) 为从终点 \(v\) 跳到当前的 \(v\) 的答案。每一次如果是 \(u\) 跳就让 \(l\gets \text{merge}(l,ans)\),否则就是 \(r\gets \text{merge}(ans,r)\),要注意顺序。这个 \(\text{merge}\) 的方式就是上面合并左右儿子的一样的操作。
这样就可以通过了,时间复杂度 \(O(n\log^2n)\)。然后注意一些 unsigned long long 的细节即可。
也就码了 4KB 而已,侥幸冲进最优解第一页。
18. CF1198D Rectangle Painting 1
难度:1
首先发现最终答案一定 \(\le n\),这个没得说。
现在考虑一个 \(h\times w\) 的矩形,则它的答案一定 \(\le \max(h,w)\)。因为可以直接全涂了。
那么什么情况下可以不用全涂呢?会发现至少有一行或一列没有被涂可以不用全涂,否则还不如全涂。
所以从这上面出发去思考。发现数据范围很神啊,\(n\le 50\),可能是一个至少 \(O(n^4)\) 的算法。
设 \(dp_{i,j,k,l}\) 表示使得左上角为 \((i,j)\),右下角为 \((k,l)\) 的矩形合法的最小代价。
怎么转移呢?
首先考虑全涂,则有 \(dp_{i,j,k,l}=\max(k-i+1,l-j+1)\)。
如果不是全涂则一定有一行或一列没被涂(这里的一行是在该矩形内,而不是整个矩形的一行,列也同理)。考虑二维区间dp,枚举没被涂的那一行或那一列,然后将该矩形分成上下或左右两个矩形(可能有一个长或宽为 \(0\) 的矩形),则 \(dp_{i,j,k,l}\) 的值是这两个矩形的 \(dp\) 相加的最小值。
那么没被涂的这一行或这一列需要满足什么要求呢?也就是这一行或这一列没有黑格子即可。用二维前缀和维护。
初始化:如果 \(a_{i,j}=\#\),则 \(dp_{i,j,i,j}=1\);否则 \(dp_{i,j,i,j}=0\)。
答案为 \(dp_{1,1,n,n}\)。
然后对于枚举矩形的顺序问题。我们可以把所有矩形预处理出来再按它们的面积大小从小到大枚举转移即可。因为这个矩形的数量大约在 \(3\times 10^6\) 左右,可以排序。
时间复杂度 \(O(n^5+n^4\log n)\),常数极小。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号