atcoder agc039c Division by Two with Something 题解

题目链接

以下称 \(k\) 的二进制数构成的串（也就是被操作的串）为原串，如果不足 \(n\) 位则在前面补 \(0\) 补成 \(n\) 位。

首先转化操作，可以理解为将 \(k\) 的最后一位取反放在开头并将 \(k\) 右移一位。

我们操作一个数会进入一个循环，如

\[110101 \to 011010 \to 101101 \to 010110\to 101011\to 110101 \]

而我们求的答案就是在 \([0,x]\) 中每个数所在循环的大小之和。

上面这样写可能有点不好看，那如果我们不右移呢？这样我们最终会形成一个长度为 \(2n\) 的 \(01\) 串，其中后 \(n\) 位为原串，前 \(n\) 位为原串取反后的串。

如 \(110101\) 生成为 \(001010110101\)。那么循环内的所有数实际上就是该长度为 \(2n\) 串的长度为 \(n\) 的子串。

如刚才那个例子：

\[001010[110101]\\ 00101[011010]1\\ 0010[101101]01\\ 001[010110]101\\ 00[101011]0101\\ 0[010101]10101\\ [001010]110101 \]

有点类似一个滑动窗口吧。这个循环长度为 \(6\)，所以说可能存在操作串所在循环长度为 \(n\)。

我们再举一个例子：

\(010\) 生成 \(101010\)，而它所在循环是 \(010\to 101\to 010\)长度为 \(2\)，并不是 \(n=3\)。

原因是有子串 \(1[010]10=101[010],[101]010=10[101]0\)，也就是说该 \(2n\) 串的循环周期小于 \(2n\) 了，使得该串的子串出现重复了。

我们设 \(T\) 为这个 \(2n\) 串的循环最小正周期。所以有 \(T\mid 2n\)，而又因为这个串的前 \(n\) 位是由后 \(n\) 位取反而来的，不相等。因此有 \(T\nmid n\)。所以可以得出 \(T\) 一定是偶数。

再者，画一下图就知道 \(\frac{2n}{T}\) 为奇数，不然无法满足 \(T\nmid n\)。因为如果 \(\frac{2n}{T}\) 为偶数，则一定可以将原串（也就是后 \(n\) 位）分为 \(\frac{2n}{2T}\) 个周期，不满足 \(T\nmid n\)。

因为 \(T\) 是偶数，所以将每个周期拆成 \(A+A'\) 两个长为 \(\frac{T}{2}\) 的子串。然后有以下推导：

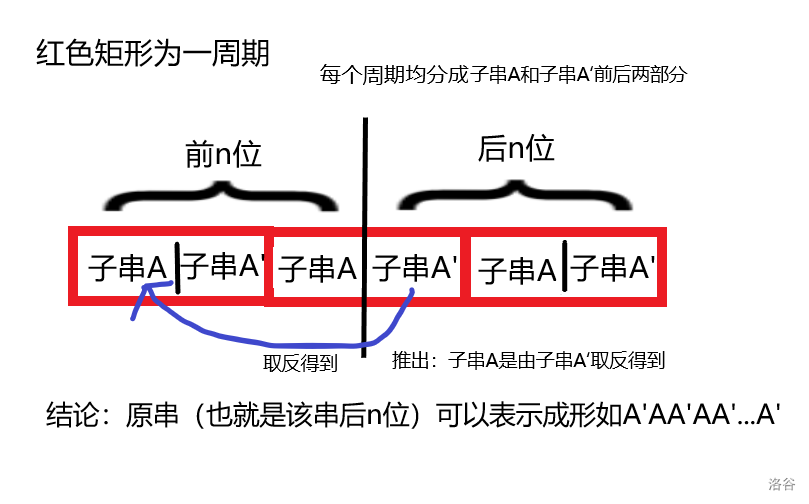
再解释一下这个图。我们将每一个周期均分成前后两部分 \(A\) 和 \(A'\)。则最中间的周期的 \(A\) 部分会在前 \(n\) 位，\(A'\) 部分会在后 \(n\) 位。而根据这个 \(2n\) 串的生成方式，这个周期的 \(A'\) 取反得到了第一个周期的子串 \(A\)。而又因为每一个周期的 \(A\) 都相等，所以得出 \(A'\) 和 \(A\) 可以互相通过取反得到。后 \(n\) 位（原串）是由 \(A'AA'...A'\) 构成的，所以后 \(n\) 位可以拆分成奇数个长度为 \(\frac{T}{2}\) 的子串，且相邻子串可以互相通过取反得到。

那么接下来，我们考虑如何统计答案。

首先先枚举 \(T\)，需要满足 \(T\mid 2n\) 且 \(T\nmid n\)。然后记 \(len=\frac{T}{2}\)，所以子串 \(A'\) 长度为 \(len\)。

但是原串有大小限制，必须在 \([0,x]\) 之间，这怎么处理呢？

我们想到如果 \(A'\) 定了，那么原串就定了。而又因为 \(A'\) 是在原串的开头，所以只要 \(A'\) 小于输入串的前 \(len\) 位，就可以原串就小于输入串。

而当 \(A'\) 与输入串的前 \(len\) 位相同时，因为 \(A'\) 已定，所以直接将整个原串求出再与输入串比较。而这样的 \(A'\) 只有一个，所以可以直接暴力判断。

我们设 \(k\) 为 \(A'\) 对应的二进制串转化为十进制后的值。我们直接让 \(A'\) 等于输入串的前 \(len\) 位从而生成出原串，然后判断原串与输入串的大小，如果原串不大于输入串，则有 \(k+1\) 个 \(A'\) 合法（别忘了全 \(0\) 串哦）；否则有 \(k\) 个 \(A'\) 合法。

记 \(f_i\) 为 \(T=i\) 时合法的 \(A'\) 的数量，\(f_i\) 求法上一段已给出。

但是还可能重复。如原串长为 \(3\)，那么合法周期可以是 \(2\) 和 \(6\)，会重复计算。

我们只用最小合法正周期计算答案，所以在用 \(i\) 计算答案时，要枚举它的倍数 \(j(j\neq i)\)，让 \(f_j\gets f_j-f_i\)。

则最终答案为 \(\sum_{T\mid 2n且T\nmid n}T\times f_T\)。

通过暴力计算，合法的 \(T\) 的个数不超过 \(64\)，所以时间复杂度能过。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=4e5+5,mod=998244353;
#define int long long
int n,a[N],f[N],ans,tmp[N];
int read()//快读 
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
signed main()
{
	n=read();
	for(int i=1;i<=n;i++)
	{
		char w;
		cin>>w;
		if(w=='1') a[i]=1;
	}
	int cnt=0;
	for(int T=2;T<=2*n;T+=2) 
	{ 
		if(n%T==0) continue;
		if((2*n)%T) continue;//找到合法的T 
		int num=0,len=T/2;//num为合法的A'的个数 
		for(int j=1;j<=len;j++) num=(num*2+a[j])%mod,tmp[j]=a[j];
		
		//tmp为 与输入串前len位相同的A' 生成的原串 
		for(int j=len+1;j<=n;j++) tmp[j]=tmp[j-len]^1;
		bool flag=1;
		for(int j=len+1;j<=n;j++)
		{
			if(tmp[j]>a[j]){flag=0;break;}
			if(tmp[j]<a[j]) break;
		}//判断大小 
		pre+=flag; //因为要包括00000...所以要改为如果小于等于就+1 
		
		f[T]=(f[T]+num)%mod;
		
		for(int j=2;T*j<=2*n;j++) f[T*j]=(f[T*j]-f[T]+mod)%mod;//容斥 
		
		ans=(ans+f[T]*T)%mod;//统计答案 
	}
	printf("%d\n",ans);
	return 0;
}