2024.12 做题记录
难度评级 \(x\):
\(x\in[0,1]\): 自己切了(记思考过程)
\(x\in(1,2]\): 有思路,看题解懂了(记自己思路与正解)
\(x\in(2,3]\): 完全没思路(记正解)
1. AT_arc189_b Minimize Sum
难度:1
我先从前缀和、差分等角度去看这个问题,发现可能差分会直观一点。
假设我们选择了 \(\{x,x+a,x+a+b,x+a+b+c\}\) 这四个数进行操作,则会变成 \(\{x,x+c,x+c+b,x+a+b+c\}\)。二者之和相减得到贡献增加了 \(2(c-a)\)。
记 \(b_i=a_{i+1}-a_i\)。
那么对应到差分数组就是 \(\text{swap}(b_i,b_{i+2} )\) 的代价为 \(-2(b_i-b_{i+2})\)。
所以按奇偶分开讨论。我们想让结果最小,所以在 \(b_i>b_{i+2}\) 的 \(i\) 都进行 \(\text{swap}(b_i,b_{i+2} )\)。实际上也就是交换一次,逆序对个数减一,所以答案为 \(\sum_{i=1}^{n} a_i-2\times \max(0,b_x-b_{y})\),\(x,y\)满足 \(x\equiv y(\bmod\ 2)且x<y\)。
可以用树状数组维护,赛时写的这个。
其实最后结果就是所有 \(i\) 为偶数的 \(b_i\) 单调不降,奇数也一样。我们就知道了所有的 \(b_i\),再求出所有 \(a_i\) 再加和即可。
时间复杂度 \(O(n\log n)\)。瓶颈在排序。
2. CF2040D Non Prime Tree
难度:2
构造题,恶心。
直接去搜会炸,考虑性质。发现 \(2\) 是个非常特殊的质数,如果让差为偶数则只需要让差不为 \(2\) 即可。赛时考虑所有点全填偶数,然后被菊花图卡住了。
实际上,我们随便选择一条边,将其断开,使得原树变成两棵树。那么此时能否考虑一棵全填奇数,一棵全填偶数。
现在只考虑偶数,为了让任意一条边的两个点的差不为 \(2\),所以考虑将该树重新按深度分一下,深度为 \(1\) 的点从最小的没填的偶数开始填,深度为 \(2\) 的点从最大的没填的偶数开始填,深度为 \(3\) 的点再从最小的没填的偶数开始填......以此类推。
因为该树最大只有 \(n-1\) 个节点,所以中间总有一个数不会被填,且深度差为 \(1\) 的点的值分别大于它和小于它,则它们的差 \(\ge 4\)。是合法的。
另一棵树同理填入奇数。
刚好两棵树的根填了 \(1\) 和 \(2\),是合法的。
时间复杂度 \(O(n)\)。
3. P3188 [HNOI2007] 梦幻岛宝珠
难度:1
自己想的,数据范围很妙啊。
题意就是一个普通的01背包,但是 \(w\le 2^{30}\),开不下乐。
这道题唯一的特点就是 \(w_i=a\times 2^b,a\le 10 ,b\le 30\)。要从这里找突破口。启发我们从二进制位数上考虑。
我们可以找到每一个 \(w_i\) 对应的 \(b\),所以可不可以理解为在第 \(b\) 位上占了 \(a\) 的空间。如果从大到小考虑,有点难搞,不妨从小到大考虑位数。每一位都有一个空间上限,记为 \(mx_i\) ,则有 \(mx_i=m>>i\)。
所以设 \(dp_{j,i}\) 表示在 \(2^i\) 选了 \(j\) 空间的最大价值。每一位的空间最多是 \(n\times a=10^4\),所以空间开的下。
则转移为:
但是这样有个问题。就拿样例来说吧。
总容积 \(m=10=(1010)_2\),有物体 \(w_i=5=(101)_2\times 2^0,v_i=8\),则 \(mx_0=10\)。
能不能选这个物体呢,显然是可以的,因为 \(5<10\) 。转移后 \(dp_{5,0}=8\),再转移有 \(dp_{2,1}=8\)
但是有个问题,选了过后又有物体 \(w_j=6=3\times 2^1=(110)_2\times 2^1,v_j=11\),\(mx_1=5\)此时从 \(dp_{2,1}\) 转移时因为 \(2+3\le 5\),所以可以转移到 \(dp_{5,1}=19\)。
这时你会发现 \(w_i+w_j=5+6=11>10\)。不对啊,怎么还超出了容积呢?
仔细查了查,发现因为 \((5>>1)=2\neq \frac{5}{2}\),所以 \(5\) 多出来的 \(1\) 被我们吃掉了(别说,还挺香)。此时只有当 \(w_j<mx_1\) 时我们才能取 \(j\) 这个物品。
怎么解决这种情况呢?考虑多加一维状态。
记 \(dp_{j,i,0/1}\) 表示第 \(i\) 位,占了 \(j\) 的容积并且能/否占用 \(mx_i\) 的空间。
其实也就是如果二进制下 \(m\) 的第 \(k\) 位为 \(0\) ,但我们最终造成的贡献在该位为 \(1\) 的情况。换一种理解方式,也就是 \(j\) 的后 \(i\) 位组成的数 \(J\) 与 \(m\) 的后 \(i\) 位组成的数 \(M\) 相比,\(J\le M\)(对应状态为 \(0\))或 \(J> M\)(对应状态为 \(1\))。
所以考虑更改一下转移:
然后在进位时需要分类讨论:
-
二进制下 \(m\) 的第 \(i\) 位为 \(0\) ,\(j\equiv 1(\bmod\ 2)\)。此时是从 \(0/1\to 1\)。
\[\\ dp_{j,i,0}\to dp_{j>>1,i+1,1},j\in[0,mx_i]\\ dp_{j,i,1}\to dp_{j>>1,i+1,1},j\in[0,mx_i] \] -
二进制下 \(m\) 的第 \(i\) 位为 \(1\) ,\(j\equiv 0(\bmod\ 2)\)。此时是从 \(0/1\to 0\)。
\[\\ dp_{j,i,0}\to dp_{j>>1,i+1,0},j\in[0,mx_i]\\ dp_{j,i,1}\to dp_{j>>1,i+1,0},j\in[0,mx_i] \] -
二进制下 \(m\) 的第 \(i\) 位与 \(j\) 的最后一位相同(也就是除了上述两种情况之外)。此时是从 \(0\to 0,1\to 1\)。
\[\\ dp_{j,i,0}\to dp_{j>>1,i+1,0},j\in[0,mx_i]\\ dp_{j,i,1}\to dp_{j>>1,i+1,1},j\in[0,mx_i] \]
最终答案为 \(\max_{i=1}^{30}\max_{j=0}^{mx_i}dp_{j,i,0}\),也就是所有合法的值的最大值。
时间复杂度 \(O(Tnb\min(10^3,W))\),空间复杂度 \(O(nab)\),前者最高 \(6\times 10^7\),后者最高 \(6\times 10^4\)。
OS:好像可以向上取整
4. CF864F Cities Excursions
难度:2
模拟赛考了,放的 \(T1\)(赛后才知道),以为是P9981 [USACO23DEC] Minimum Longest Trip G,赛时挂了,后面发现不一样。
有种暴力做法,对于询问 \((s,t,k)\),建反向图从 \(t\) 出发标记所有能到的点,然后处理出原图每个点能到的最小且可达 \(t\) 的点,然后从 \(s\) 开始搜索,每一次按处理的跳,跳到环上就输出 \(-1\),直到跳到 \(t\),然后输出。时间复杂度 \(O(nq)\),在常数加持下约为 \(1.6\times 10^9\),能拿部分分。
考虑优化常数,发现 \(n\le 3000\) 却 \(q\le 4\times 10^5\),所以考虑将 \(t\) 一样的询问一起处理,这样只用标记 \(n\) 次能到达 \(t\) 的点。这样时间复杂度 \(O(nq)\),运算约为 \(8\times 10^8\),卡一卡数据水的话可以卡过去。
然后是正解。
在暴力做法2的基础上进行优化,枚举 \(t\),处理每个点的后继点,如果将每个点与它的后继点连边,整个图会变成一个内向基环树。
对每个点开一个vector,存入 \(s_j=u\) 的的询问(询问的 \(t\) 与枚举的 \(t\) 相等)。
同样,对该图建反图,从 \(t\) 开始进行深搜,同时开一个栈 \(st\) 存下 \(t\) 到当前节点的路径上的点。枚举该节点的vector的所有询问,如果 \(k\le top\),则答案为 \(st_{top-k+1}\)。
对于没有被更新答案的询问输出 \(-1\)。
时间复杂度 \(O(n^2+q)\)。
5. P3287 [SCOI2014] 方伯伯的玉米田
难度:2.5
首先有一个结论:对于每一次拔高,拔高一个后缀一定更优。我们可以先把要拔走的所有玉米全部拔去,剩下的玉米就直接拔高后缀明显更优。
所以设 \(dp_{i,j}\) 为第 \(i\) 棵玉米,被拔高了 \(j\) 次的答案。
则有转移:
直接暴力是 \(O(n^4)\)。考虑优化,这个东西有点三维偏序的感觉,感觉可以cdq,但还是先冷静一下,因为我不怎么会cdq。
首先 \(k<i\) 的限制只要我们正序枚举就能满足。然后后面是一个二维偏序问题,考虑转化为坐标系上的问题。对于 \(dp_{i,j}\) ,将其放在 \((j,a_i+j)\) 处,这样更新 \(dp_{i,j}\) 时,就只用找 \((j,a_i+j)\) 左下角矩形里的最大值就行了,用二维树状数组处理。
然后二维树状数组就是在一维循环内部再套一个树状数组就行了,修改查询都是 \(O(\log^2n)\)。
本题时间复杂度 \(O(nk\log^2n)\)。
6. P3506 [POI2010] MOT-Monotonicity 2
弱化版难度:1
强化版难度:3
先说弱化版P3541 [POI2010] Monotonicity。
\(n\le 2\times 10^4,k\le 100\)。一眼应该是dp。
设 \(dp_{i,j}\) 表示 \(a_i\) 是第 \(p\) 个取的, \(p\equiv j(\bmod\ k)\)。
则有转移:
\(a_i\) 与 \(a_p\) 的关系满足 \(s_j\) 的字符。
直接转移是 \(O(n^2k)\),考虑用线段树优化,时间复杂度 \(O(nk\log n)\)。因为要开 \(k\) 棵线段树,所以需要 \(a_i\) 离散化一下。
再说强化版。
\(n,k\le 5\times 10^5\),这咋做?如果用二维dp,怎么搞都有一个 \(O(nk)\),直接寄掉。
只能一维了,并且还要在 \(O(\log n)\) 左右进行转移,可能要用线段树什么的搞一下。
可以发现如果想从 \(j\) 转移到 \(i\) ,一定是从 \([1,j]\) 中选出的最长序列转移过来的,这样是不劣的。可以感性理解一下。
所以对于 \(i\in[1,n]\),处理出 \(dp_i\) 后,想要往后转移就必须保证 \(i,j\) 的关系是等于 \(s_{dp_i\% k}\) 的,所以开两个线段树(好像树状数组也行),分别处理 < 和 > 的情况,对于 = 的情况,开一个桶就行了。
时间复杂度 \(O(n\log n)\)。
7. AT_arc057_d 全域木
难度:3 \(\to\) 2
没思路,题解点一下就懂了,一些细节(包括实现)是自己想的。
模拟赛考了,数据范围是 \(n\le 40\),原题(也就是该题)数据范围为 \(n\le 30\)。实际上两种都能过。
又是计数题,有点不会。
考虑按边权从小到大枚举每一条边,每一条边有两种状态,一是树边,二是非树边。
类似Kruskal的算法流程,每一次加树边可以理解为将两个联通块连成一个联通块,加非树边就是在一个联通块中加边。
发现 \(n\le 40\) ,数据范围非常小。我们可不可以把所有联通块的状态记下来?开若干个长为 \(n\) 的数组 \(b\),\(b_i\) 记的是当前状态下有几个大小为 \(i\) 的联通块。
状态数是 \(40\) 的拆分数,也就是将 \(40\) 拆成若干个正整数之和的方案数,可以暴力跑一下, \(P(40)\approx 3\times 10^4\)。
将所有状态搜索出来,用结构体存下。
接下来模拟加边过程,设 \(dp_{i,j}\) 为在加边权为 \([1,i]\) 的边后状态为第 \(j\) 个状态的方案数。
- 如果当前边是非树边,实际上就是联通块内部连边。在联通块中选一个联通块中的两个点连起来,还要去掉之前的非树边(别选重了),则有如下转移:
\(\ \ \ \ \ \ b_{j,k}\) 表示在第 \(j\) 个状态下的 \(b\) 数组的第 \(k\) 位。
\(\ \ \ \ \ \ \sum_{k=1}^{n} C_{b_{j,k}}^2\) 的值可以提前预处理出来。
-
如果当前边是树边,也就是对两个联通块进行连边,需要从一种状态转移到另一种状态。因为有 \(m=\frac{n(n-1)}{2}\) 条边,也就是需要转移 \(m\) 次,所以转移到状态需要预处理出来,不然会求 \(m\) 次。
为了方便,我们记数组 \(hsh_i\),这是一个和哈希数组,是一个在 \([1,2^{31}-1]\) 的随机正整数。对于一个状态,他的哈希值 \(sum\) 为 \(\sum_{i=1}^{n} hsh_i\times b_i\),这样我们就可以用
map/unordered_map将一个状态(\(b\) 数组的值)与它的编号建立双射。所以对于一个状态,找到变量 \(j,k\in[1,n],j<k,b_j\neq 0.b_k\neq 0\),则他可以转移到 \(sum\) 值为 \(sum_i-hsh_j-hsh_k+hsh_{j+k}\) 的状态上去,并乘系数 \(b_j\times b_k\times j\times k\)。
我们可以将这种转移关系用带权有向边表示出来,系数放在边权上。
转移的时候,枚举边的到达点 \(k\),设该边边权为 \(w\),则有转移:
\[dp_{i,k}\gets dp_{i-1,j}\times w \]
这样就是所有转移。
初始化:设状态 \(j\) 满足 \(sum_j=hsh_1\times n\),则有 \(dp_{0,j}=1\)。其余状态全部初始化为 \(0\)。
答案:设状态 \(j\) 满足 \(sum_j=hsh_n\),则答案为 \(dp_{m,j}\),其中 \(m=\frac{n(n-1)}{2}\)。
时间复杂度 \(O(P(n)m+P(n)n^2)\),后者带一个 \(\frac{1}{2}\) 的常数,总体还要再乘上一个map/unordered_map的时间复杂度,大约是 $10^8 $ 次运算。
空间复杂度 \(O(P(n)n+P(n)m)\),前者是存状态的结构体数组,后者是 \(dp\) 数组。
跑得飞快,拿下了当时的最优解。
8. UVA11149 Power of Matrix
难度:3 $\to $ 2.5
没想到。
可以倍增去做,但是有没有其他做法?
设 \(S_i=\sum_{j=1}^{i}A^j\),我们求的就是 \(S^k\)。
暴力是 \(O(n^3k)\),会挂。直接用矩阵快速幂去求 \(S\) 是很难的,因为 \(S_i\) 是由 \(A_i\) 得来的,所以考虑把 \(S_i\) 和 \(A_i\) 放在一个矩阵里去求。
这样,这个矩阵就是一个复合矩阵,也就是矩阵套矩阵。
我们设 \(I_n\) 为 \(n\times n\) 的单位矩阵,\(E_n\) 为 \(n\times n\) 的全 \(0\) 矩阵。则有如下转移:
这样的话就可以进行矩阵快速幂了,不过要写两遍,因为是矩阵套矩阵。
最后把 \(S_i\) 输出就行了。
本题主要难在实现。
9. P6569 [NOI Online #3 提高组] 魔法值
难度:1.2
首先可以猜一下,在 \(t\) 时刻 \(j\) 的值应该等于 \(\text{xor}_{i=1}^{n} f_i\times [i 到 j 长度为 t 的路径数为奇数]\)。
所以可以考虑搞一个矩阵 \(A\),\(A^k_{i,j}\) 记录的是 \(i\) 到 \(j\) 长度为 \(k\) 的路径数,这个路径数是在模 \(2\) 意义下进行计算的。
然后对于每一次询问,我们求出它对应的矩阵,然后遍历这个矩阵,如果 \(A_{j,1}=1\),则 \(ans\gets ans \ \text{xor}\ f_j\)。
然后更新矩阵时,用倍增去更新,也就是处理出 \(A^k,k\in[0,31]\)。
这样做时间复杂度是 \(O(n^3\log V+qn^3\log V+qn^2)\),然后超时的部分是 \(O(qn^3\log V)\),瓶颈在于倍增求答案矩阵。
怎么去优化这个呢?它的运算次数大约为 \(3\times 10^9\)。如果能不能套一个小于 \(1\) 的常数,看一下能不能过。
怎么弄呢?发现 \(A\) 矩阵一直是一个 \(01\) 矩阵,考虑用 bitset 优化矩阵乘法。
在本题中矩阵乘法可以转化为位运算为 \(A_{i,j}=\text{xor} \ (B_{i,k} \ \ \text{and}\ \ C_{k,j})\)。
我们知道矩阵乘法是将一个矩阵的一行与另一个矩阵的一列相乘。如果我们能用整行和整列进行位运算操作,这样就会有一个 \(\frac{1}{w}\) 的常数。
所以考虑对于每一个矩阵,我们对行和列各开 \(n\) 个 bitset 存下来它的这一列/这一行的值,行记为 \(h_{i,j}\),列记为 \(l_{j,i}\)。
这样的话,矩阵乘法就相当于 \(h_{i} \ \text{and} \ \ l_{j}\),而被更新的值 \(A_{i,j}\) 的值要取决于 \(h_{i} \ \text{and} \ \ l_{j}\) 后得到的bitset 中 \(1\) 的奇偶, \(A_{i,j}\) 与它奇偶性相同。
每一次更新都要同时更新行和列的值。
这样时间复杂度就是 \(O(\frac{n^3\log V}{w}+\frac{qn^3\log V}{w}+qn^2)\),可以通过。
10. P9017 [USACO23JAN] Lights Off G
难度:1
12.24模拟赛T2
首先可以发现操作二等同于 \(a\) 异或上 \(b\) 数组。所以考虑能不能让三个操作都在二进制意义下进行。那么答案就是最小的操作次数使得 \(a\ \text{xor}\ b=0\),也就是 \(a=b\)。
然后答案应该是有一个上界的,应该是 \(n\) 乘上一个小系数。经对拍,应该
所以考虑枚举答案 \(k\),看一看进行 \(k\) 次操作的异或式子是什么。我们记 \(b\to k\) 为对 \(b\) 数组进行 \(k\) 次操作 \(3\) (向右循环)后的二进制数。对于每一次操作,我们都会使 \(b\) 中一位的值翻转,我们记数组 \(c\),\(c_i\) 为第 \(i\) 次操作翻转了 \(b\) 的第 \(c_i\) 位,也就是异或上了 \(2^{c_i}\)。
那么对于 \(b\ \text{xor}\ 2^{c_i}\),我们对其循环 \(1\) 次后是 \((b\ \text{xor}\ 2^{c_i} )\to 1=(b\to 1)\ \text{xor}\ (2^{c_i}\to 1)\ \text{xor}\ 2^{c_i}\),也就是 \((b\to k)\) 异或上 将 \(2^{c_i}\) 向右循环扩展 \(k\) 次的值,我们记为 \((c_i \ \rhd\ k)\)。
举个例子:
设 \(b=10000000\),\(c_1=3\),则 \(b\ \text{xor}\ 2^{c_1}=10001000\),\((b\ \text{xor}\ 2^{c_1})\to 1=11001100\),\(((b\ \text{xor}\ 2^{c_1})\to 1)\to 1=11101110=(b\to 3)\ \text{xor}\ 2^{c-1}\ \text{xor}\ (2^{c-1}\to 1)\ \text{xor}\ (2^{c-1}\to 2)=(b\to 3)\ \text{xor}\ (c_1 \ \rhd\ 2)\)。
因为更改 \(a\) 数组是在操作 \(2\),于是我们将这一次的操作 \(3\) 归到下一次操作,所以以下的 \(k\) 次操作实际上只有 \(k-1\) 次操作 \(3\)。
当 \(k=1\) 时,有 \(b'=b\ \text{xor}\ 2^{c_1}\)。
当 \(k=2\) 时,有 \(b'=((b\ \text{xor}\ 2^{c_1})\to 1)\ \text{xor}\ 2^{c_2}=(b\to 1)\ \text{xor}\ (c_1\rhd 1)\ \text{xor}\ 2^{c_2}\)
当 \(k=3\) 时,有 \(b'=((((b\ \text{xor}\ 2^{c_1})\to 1)\ \text{xor}\ 2^{c_2})\to 1) \text{xor}\ 2^{c_3}=(b\to 2)\ \text{xor}\ (c_1\rhd 2)\ \text{xor}\ (c_2 \rhd 1)\ \text{xor}\ 2^{c_3}\)。
所以当 \(k=x\) 时,有 \(b'=(b\to k-1)\ \text{xor}\ (\ \text{xor}_{i=1}^{x}\ (c_i\rhd k-i))\)。
而对于 \((b\to k-1)\) 是可以 \(O(n^2)\) 预处理出来的。那么后面的那一坨跟 \(b\) 没有关系,而题目又有所有的 \(n\) 都相等这一性质,所以可以在所有询问前处理出来。
用状压dp,时间复杂度 \(O(n^22^n)\)。
所以对于每一次询问,枚举 \(k\),判断 \(a\ \text{xor}\ (b\to k-1)\) 是否能在 \(\{c_1,c_2...,c_k\}\) 中凑出来。
时间复杂度 \(O(n^22^n+qn^2)\),空间复杂度 \(O(n2^n+n)\)。
难度应该是上位蓝/下位紫。
11. P4065 [JXOI2017] 颜色
难度:1
12.24模拟赛T4
赛时切的第一道紫&&第一道省选!
首先转化以下求的问题,其实是求 \(\sum_{l=1}^{n}\sum_{r=l}^{n}[所有在[l,r]出现的颜色的同色点全部在[l,r]]\)。
所以可以用前缀和求出每一种颜色出现次数,然后枚举区间、颜色,依次判断,时间复杂度 \(O(n^3)\),期望得分 \(40pts\)。
记录 \(R_i=\max_{j=i}^{n}j\times [a_j=a_i]\),\(L_i=\min_{j=1}^{i}j\times [a_j=a_i]\)。也就是同颜色的最左最右点。
考虑枚举左端点 \(l\),右端点用指针往右跳,如果区间 \([l,r]\) 满足 \(\max_{j=l}^rR_j\le r\) ,那么说明所有在该区间里出现过的颜色的最右点都被区间包括了,但是最左点呢?
所以还需满足 \(\max_{j=l}^rL_j\ge l\)。这两个都可以用双指针/st表维护。
时间复杂度 \(O(n^2)\),期望得分 \(60pts\)。
正解:
我们还是枚举左端点,但是上述的判断太慢了。如何更快?
首先有一个结论,就是所有合法区间的左端点一定是它的颜色的第一个点,也就是它前面没有与它同色的点。
因为如果有同色,那么 \(a_l\) 不可能全部都在 \([l,r]\) 内,所以都不合法。
同样,每一个合法区间右端点都是一个颜色最右的那个点。
所以有 \(l_i=i\)。我们需要使得 \(\max_{j=l}^rL_j\ge l\),也就是 \(\max_{j=l}^rL_j\ge L_i\),这里就可以直接对于每一个 \(i\) 用单调栈预处理出最右的 \(j\),记为 \(nxt_i\)。所以右端点只用考虑 \([l,nxt_l-1]\) 就行了。
记权值数组 \(val\)。所以考虑倒序枚举左端点 \(l\),如果当前点是某个颜色的最右点则 \(val_l=1\),否则 \(val_l=0\)。
但是有问题。如样例 \(3\ 2\ 4\ 3\),如果 \(l=1\),那么在 \(r=2或3\) 是都不合法。所以在枚举 \(l\) 时,每一次还要对 \([l,R_l-1]\) 进行区间赋值为 \(0\)。
如果当前点是某个颜色的最左点,则答案加上 \(\sum_{j=l}^{nxt_l-1}val_j\)。
那么区间求和,区间赋值,用线段树/珂朵莉树维护。
时间复杂度 \(O(n\log n)\)。
12. CF2043E Matrix Transformation
难度:3
被CD卡了,没时间(或者说没实力)做E。
首先,这种位运算的题就要考虑按二进制的每一位单独讨论,只要位与位之间不互相影响就行。
所以依次讨论每一位,发现 \(a,b\) 矩阵都变成的\(01\)矩阵。我们只用讨论这一行需要几次按位与 \(0\) 和这一列需要几次按位或 \(1\)。
接下来该怎么做呢?我们先举一个例子:
\(a_{i,j}\) 为从上往下第 \(i\) 行,从左往右第 \(j\) 列。
那么 \(a_{2,2}\) 需要一次按位或 \(1\),则变成:
\(a_{2,1}\) 需要一次按位或 \(1\),则变成:
\(a_{1,1}\) 需要一次按位与 \(0\),则变成:
\(a_{1,2}\) 需要一次按位或 \(1\),则变成:
这样我们就完成了。你会发现原本有 \(a_{1,1}=b_{1,1}\),但我们在中途仍然使得 \(a_{1,1}\) 的值发生改变,所以这个操作有点像一环扣一环的形式,同一个可能会导致一些其他位置也要动的传导模式。
所以考虑建边。节点 \(i\) 表示给第 \(i\) 行进行一次按位与 \(0\) 的操作,节点 \(j+n\) 表示给第 \(j\) 列进行一次按位或 \(1\) 的操作。
讨论对于节点 \(a_{i,j}\)。
-
如果 \(b_{i,j}=1\),那么我们对第 \(i\) 行进行按位与的操作后我们一定会对第 \(j\) 列进行按位或的操作。所以连边 \((i,j+n)\)。
-
如果 \(b_{i,j}=0\),那么我们对第 \(j\) 列进行按位或的操作后我们一定会对第 \(i\) 行进行按位与的操作。所以连边 \((j+n,i)\)。
那么什么情况无解呢?
再举个例子:
那么 \(a_{2,1}\) 需要一次按位或 \(1\),则变成:
\(a_{1,1}\) 需要一次按位与 \(0\),则变成:
\(a_{1,2}\) 需要一次按位或 \(1\),则变成:
\(a_{2,2}\) 需要一次按位与 \(0\),则变成:
然后就回到了最开始的状态。所以不难理解,如果出现了无解的情况当且仅当我们走到的边形成了环。
然后就是遍历图的起点。如果 \(a_{i,j}\neq b_{i,j}\),我们就会对这里进行分类讨论:
- 如果 \(a_{i,j}=0\),则第 \(j\) 列需要按位或操作,则起点为 \(j+n\)。
- 如果 \(a_{i,j}=1\),则第 \(i\) 行需要按位与操作,则起点为 \(i\)。
但是每一个起点都跑一次dfs的话太慢了,所以建一个超级源点向这些起点连边,然后跑dfs进行判环。
时间复杂度 \(O(qnm\log V)\)。
13. CF2043F Nim
难度:3
首先Nim游戏有一个结论。对于一堆石子,每一堆有 \(a_i\) 个,如果 \(\text{xor}_{i=1}^{n}a_i=0\),则先手必败,否则先手必胜。
所以本题转化一下,相当于对于区间 \([l,r]\),求出最小的集合 \(S=\{s_1,s_2,..,s_k\}\),使得 \(\forall i\in[1,k],s_i\in[l,r]\) 且 \(\text{xor}_{i=1}^{k}a_{s_i}=0\)。求出这个最小的 \(k\) 及满足要求的 \(|S|=k\) 的 \(S\) 数量。
JMR给出了一个猫树做法,有点卡空间。设 \(d=64\)。合并是 \(O(d^2)\) ,预处理 \(O(d)\) ,时间复杂度 \(O(nd\log n+q(\log n+d^2))\)。空间复杂度 \(O(nd^2\log n )\)。靠一些优化可以卡过空间。
但是有更优方法。
首先,如果有 \(\exist i\in[l,r],a_i=0\),则 \(k=1\),方案数为这样的 \(i\) 的个数。先把这种情况判掉。
然后,而当 \(i,j\in[l,r]\) 满足 \(i\neq j\) 且 \(a_i=a_j\) 时,\(k\) 最小值为 \(2\),而答案为每种在 \([l,r]\) 中出现次数大于 \(2\) 的数中选两个。
所以用前缀和处理出前缀中每种颜色的出现次数,用来判掉上面两种情况。
因为有 \(a_i\le 50\),根据抽屉原理,如果上述两种情况都不是的询问区间长度一定 \(\le 50\),就可以直接用dp暴力跑。时间复杂度 \(O(qdV)\),运算次数为 \(3\times 10^8\),完全跑得过。
14. P10597 BZOJ4665 小 w 的喜糖
难度:2
感觉式子很怪,所以看了题解。
首先发现正难则反,所以考虑求至少有 \(k\) 个人相同,再根据二项式反演求出恰好有 \(0\) 个人相同时的答案。
因为糖果可能相同,而直接依靠推式子去求 \(k\) 个人相同又很难,所以考虑背包dp。
设 \(dp_{i,j}\) 表示考虑种类为 \([1,i]\) 的喜糖,有 \(j\) 个人相同的情况,\(x_i\) 为种类为 \(i\) 的糖个数,\(y_i\) 为种类为 \(i\) 的糖被选定相同的个数。
则没被选定的糖就是一个选多重集,所以对于一组 \(y\),答案为:
所以转移为:
初始化 \(dp_{0,0}=1\)。
还要将 \(dp_{m,j}\gets dp_{m,j}\times (n-j)!\),其中 \(m=\max_{i=1}^{n}a_i\)。
然后再用二项式反演求出答案:
时间复杂度 \(O(n^2)\)
15. CF1400G Mercenaries
难度:1.2
一眼容斥。考虑枚举一共选多少个人,用 \(O(m2^m)\) 的时间预处理出一段区间的加/减值。
拿总方案 \(-\) 冲突 \(1\) 个条件的方案数 \(+\) 冲突 \(2\) 个条件的方案数 \(-\) 冲突 \(3\) 个条件的方案数...
我们设 \(cnt_i\) 为选 \(i\) 个人时可以选的人数,这个可以用差分预处理出来。
则枚举状态 \(i\),如果二进制下第 \(j\) 位的值为 \(1\),则代表我们会使得第 \(k\) 个条件冲突,也就是第 \(k\) 个条件的两个人我们都会选。
我们将该状态下必须选的人数处理出来,设为 \(j\)。再处理出该状态所在的区间 \([L,R]\),其中 \(L=\max_{在i状态下u必须选}l_u\), \(R=\min_{在i状态下u必须选}r_u\)。记 \(w\) 为 \(i\) 中为 \(1\) 的位数。
那么对于一共选 \(x\) 个人的情况下(\(x\in[L,R]\)),则贡献为 \((-1)^w\times {cnt_x-j\choose x-j}\)。
最后答案就是所有贡献之和。
然后怎么处理这个区间和我没想好。如果用线段树,但是同一个 \(i\) 对于不同的 \(x\) 的贡献是不一样的。不好处理。
但是有一个性质就是:\(j\le 2\times m\le 40\)。
而当 \(x\) 定 \(j\) 定后,贡献不同的部分就确定下来了,所以设 \(s_{x,j}\) 为在一共选 \(x\) 个人必须选 \(j\) 个人的情况下的特殊值,这里的特殊值为 \(s_{x,j}={cnt_x-j\choose x-j}\)。然后对这个东西求一个前缀和。
然后对于每一个状态 \(i\) 的贡献就是 \((-1)^w\times (s_{R,j}-s_{L-1,j})\)。直接加起来即可。
时间复杂度 \(O(m2^m+nm)\)。
16. P4448 [AHOI2018初中组] 球球的排列
难度:1.25
首先是如何判断两个数乘积是否是完全平方数,实际上将 \(a_i\) 变成分解质因数后所有指数为奇数的质因子乘起来变为 \(a'_i\),这样如果两个数满足 \(a'_i=a'_j\),则 \(a_i\times a_j\) 是完全平方数。
现在将所有的 \(a_i\gets a'_i\),则我们需要排列 \(a_i\) 使得 \(\forall i\in[1,n-1],a_i\neq a_{i+1}\)。
这里就有两种方法了,分别从容斥和普通计数dp方向考虑。
-
法一:计数dp
考虑将所有 \(a_i\) 从小到大依次加入这个序列。
设 \(dp_{i,j}\) 表示考虑到 \(a_i\),且加入 \(a_i\) 后该序列有 \(j\) 个相邻且相同的位置。但是不好转移,考虑再加一维状态,设 \(dp_{i,j,k}\) 表示考虑到 \(a_i\),且加入 \(a_i\) 后该序列有 \(j\) 个相邻且相同且与 \(a_i\) 相等的位置,有 \(k\) 个相邻且相同且与 \(a_i\) 不等的位置。
如果插入 \(a_i\) 前序列里不存在 \(a_i\),则分类讨论:
-
如果 \(a_i\) 插入在两个相同且相邻的数中间,会导致 \(k\) 减 \(1\),所以有转移
\[dp_{i,0,j+k-1}=dp_{i-1,j,k}\times (j+k) \] -
否则则有转移
\[dp_{i,0,j+k}=dp_{i-1,j,k}\times (i-j-k) \]
如果序列里存在 \(a_i\),则记 \(las\) 为最小的位置使得 \(a_{las}=a_i\),再分类讨论:
-
如果 \(a_i\) 插入在一个与它相同数的旁边,则会导致 \(j\) 加 \(1\),则有转移
\[dp_{i,j+1,k}=dp_{i-1,j,k}\times [2(i-las+1)-j] \] -
如果 \(a_i\) 隔开了两个相同且不等于 \(a_i\) 的数,则会导致 \(k\) 减 \(1\),则有转移
\[dp_{i,j,k-1}=dp_{i-1,j,k}\times k \] -
如果上述两种情况都不符合,则有转移
\[dp_{i,j,k}=dp_{i-1,j,k}\times [i-2(i-las+1)+j-k] \]
初始化 \(dp_{1,0,0}=1\),强制将 \(a_1\) 放进去。答案为 \(dp_{n,0,0}\)。
时间复杂度 \(O(n^3)\)。
-
-
法二:容斥
考虑容斥。求出 \(g_k\) 表示至少有 \(k\) 个 \(i\) 满足 \(a_i=a_{i+1}\) 的方案数,再根据二项式反演求出恰好有 \(0\) 个相同的方案。
记 \(cnt_i=\sum_{j=1}^{n}[a_j=i]\),枚举所有的 \(i\),考虑用背包求解 \(f_k\)。设 \(dp_{i,j}\) 表示考虑到颜色 \(i\) 后已经有 \(k\) 个 \(i\) 满足 \(a_i=a_{i+1}\) 的方案数。
转移为:
\[dp_{i,k}=\sum_{j=0}^{k}dp_{i-1,k-j}\times 从cnt_i里至少有j个相同且相邻的a_i的方案数 \]因为要考虑剩下没被排的数需要全排列,则答案为:\(\sum_{j=0}^{n-1}(-1)^{j}\times {j\choose 0}\times dp_{w,j}\times(n-j)!=\sum_{j=0}^{n-1}(-1)^{j}\times dp_{w,j}\times(n-j)!\)。
那么如何求从 $ cnt_i $ 里至少有 $ j $ 个相同且相邻的 $ a_i $ 的方案数?
因为可能颜色 \(a_i\) 会被分成很多段相邻的,如 \(\{1,1,1,2,1,1\}\) 的颜色 \(1\),就被分成两段相邻的了。所以我们不能只简单地乘上 \(cnt_i\choose j+1\)。
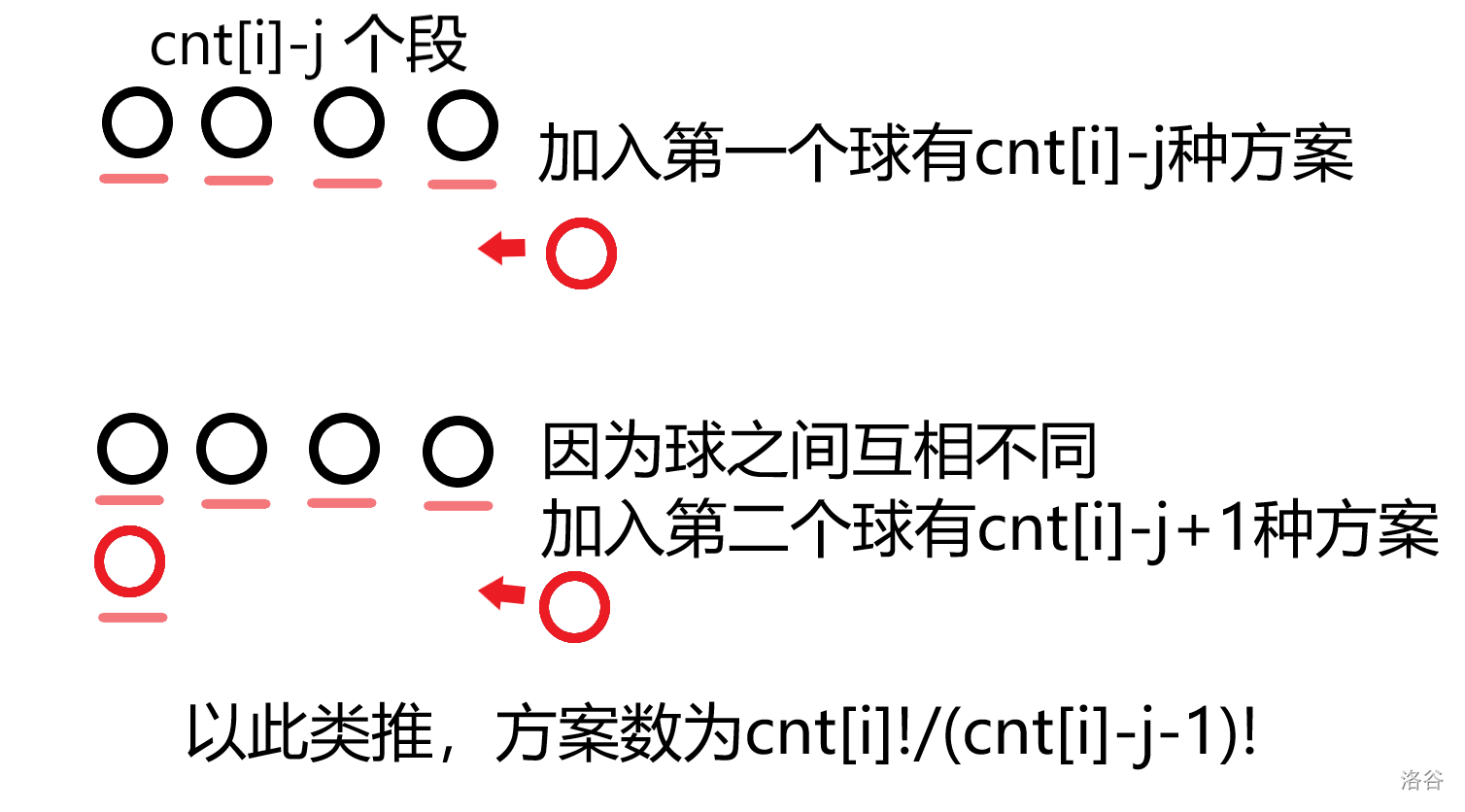
而段数是 \(cnt_i-j\) 的,我们先将所有段的起点定下来,方案数为 \(cnt_i\choose cnt_i-j\)段之间的顺序先不考虑,然后将后面 \(j\) 个点依次加入。
![]()
所以方案数为 \(C_{cnt_i}^{cnt_i-j}\times \frac{cnt_i!}{(cnt_i-j-1)!}=C_{cnt_i}^{j}\times \frac{cnt_i!}{(cnt_i-j-1)!}\),直接处理即可。所以转移为:
\[dp_{i,k}=\sum_{j=0}^{k}dp_{i-1,k-j}\times C_{cnt_i}^{j}\times \frac{cnt_i!}{(cnt_i-j-1)!} \]时间复杂度 \(O(n^2)\)。
(人傻常数大)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号