CF2042E Vertex Pairs 题解

赛时想出来了，赛后一遍过。好吧，被卡了，原因是写挂了，后面改过了。

感谢 @Akuto_urusu 提出可以优化的地方。

题意

给定一棵有 \(2\times n\) 个节点的树，每个节点都有颜色，颜色在 \([1,n]\) 之间，保证每个颜色出现 \(2\) 次。选第 \(i\) 个点的代价是 \(2^i\)。

现在，你需要选出一个集合。你需要使得这个集合内的点互相能通过该集合内的点到达，并且每种颜色都至少在该集合中出现一次。代价为集合内所有点的代价之和。

你需要找出代价最小的集合并给出方案。

思路

先考虑这个代价最小的集合的大致求法。

有一个经典技巧，从大到小考虑，如果我们选了 \(i\)，代价为 \(2^i\)，而如果我们不选 \(i\)，对于 \(j\in[1,i-1]\)，无论我们是否选 \(j\)，这个代价最多也是 \(\sum_{j=1}^{i-1}2^j=2^i-1\)，比 \(2^i\) 小。

所以按节点编号从大到小考虑，如果能不取该节点就不取（换种说法，也就是删去），否则就取。

那么什么情况下该节点可以不取呢？

根据题目给出的定义，如果删去它后有一个连通块里包含所有颜色就可以不取。

所以我们需要判断一个连通块内是否包含所有颜色。

但是，这个问题有点难解决，至少我不会。

因为删掉节点 \(u\) 后，剩下的部分有两种，一种是以 \(u\) 的儿子为根的子树，一种是整棵树删去 \(u\) 子树后剩下的部分。两种一起处理太困难了。

那么再想想，我们如何做使得只用处理一种，也就是说，另一种一定被取或被删呢？。

记 \(col_i\) 为 \(i\) 节点的颜色。

假设我们已经找到了一个必取（不可删）的节点 \(v\)，并让该连通块变成以 \(v\) 为根的树。（至于为什么是连通块而不是整个图，后面会说）

那么这样我们再考虑删点时，惊奇地发现——因为树根 \(v\) 是不能删的，所以删去的只能是子树部分。那么删去点 \(u\) 就相当于删去了以 \(u\) 为根的这棵子树！

（图为示意图，隐去了节点颜色等信息）

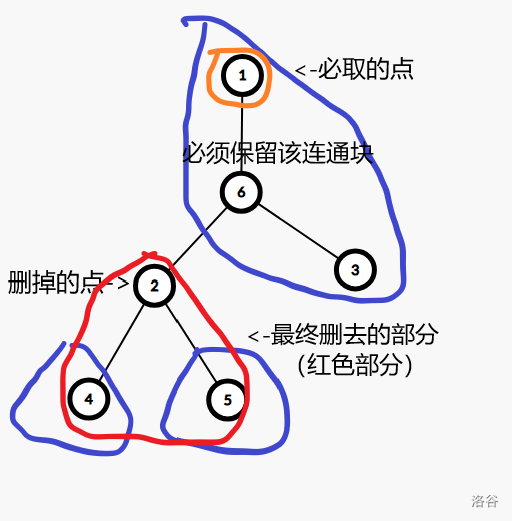
然后如何判断一个节点是否能删呢？

如果直接去搜索删完后剩下的部分是否有所有颜色太慢了，所以考虑把所有不能删的节点全部标记，没被标记的就可以删。

如果节点 \(i,j\) 满足 \(col_i=col_j(i\neq j)\)，那么 \(i,j\) 的所有公共祖先都不能删，因为如果删了，\(col_i\) 这种颜色就不存在于这个连通块中了。所以将 \(i,j\) 的所有公共祖先标记一下不能删。

但是有一些颜色初始时在这个连通块中就只有一个节点了，那么这个节点的所有祖先都不能删。

（节点黑色圆圈内为编号，圆圈外为节点的颜色）

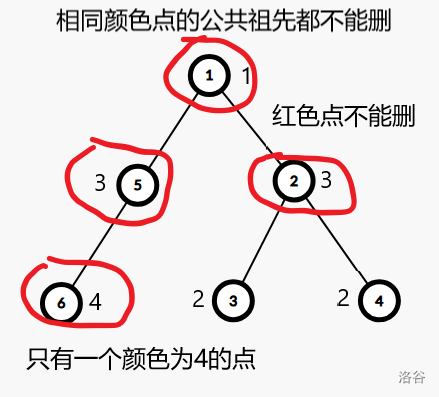
处理完后，从大到小遍历所有还没被删的点，如果没被标记就把它删掉。但是删掉该子树后，有些颜色的出现次数变成 \(1\) 了，此时仅存的那个该颜色的点的祖先都不能取。所以暴力遍历要删的子树的所有节点，对于另一个同颜色的点，对其所有祖先进行标记。

按照从大到小的顺序一直进行下去，直到所有节点被删或被标记。

那么这个标记的维护，会有路径上的更改与单点查询，考虑用树链剖分实现。因为有 \(n\) 种颜色，每种颜色需要对路径标记一次，时间复杂度为 \(O(n\log ^2n)\)。而每个节点最多被删一次，每一次删需要一次路径标记，时间复杂度为 \(O(n\log^2n)\)。到这里时间复杂度 \(O(n\log ^2n)\)。

---

现在找到一个必取点后的事情已经被我们解决了，但是如何去找一个必取点呢？

实际上，只用判断编号为 \(2n\) 的这个点是否能删就行了。

• 如果可以删，那么删完后存在唯一的节点 \(v\) 满足 \(col_v=col_{2n}(v\neq 2n)\)，而又要保证包含所有颜色，所以必须取 \(v\)。将 \(v\) 所在的连通块留下，将其他连通块删去，这也是为什么上文说的是连通块了。

• 如果不能删，那么 \(2n\) 这个点就必取，上文说的连通块在此情况下其实就是整个图。

那么如何判断编号为 \(2n\) 的点是否能删呢？

我们再来看看刚才那个图。

根据刚才说的，剩下的连通块分为两种，太麻烦了，所以初始建树时，我们钦定 \(2n\) 为树的根，这样只用讨论以 \(2n\) 的儿子为根的子树是否合法就行了。

记录 \(sum_u\) 为以 \(u\) 为根的子树内颜色种数。然后判断是否有 \(sum_v=n,v\in son_{2n}\)。

预处理 \(sum\) 数组，对于节点 \(i,j\)，满足 \(col_i=col_j(i\neq j)\)，将所有 \(i,j\) 的祖先的 \(sum\) 值加 \(1\)。这里可以用树上差分统计，将 \(sum_i\) 加 \(1\)，\(sum_j\) 加 \(1\)，\(sum_{\operatorname{lca(i,j)}}\) 减 \(1\)。

处理完后，遍历一遍树统计差分数组，然后最近公共祖先用树剖实现（因为上面已经用了树剖）。这里时间复杂度 \(O(n\log n)\)。

那么到此这道题就做完了。

所以整个做法就是：判断一下编号为 \(2n\) 的点是否能删，如果能删，将与它颜色相同的另一个点定为新树根；否则定它为新树根。然后用树链剖分处理每个点是否能删，能删则删，删后再更新标记。最后把没被删的点输出。

时间复杂度 \(O(n\log ^2n)\)，常数小，跑得挺快的。因为是树剖，所以码量可能有点大。

代码

#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize(3)
#pragma GCC optimize(2)
#pragma GCC optimize("Os")
const int N=1e6+5;
int head[N],cnt,n;//建图 
int top[N],id[N],sz[N],son[N],d[N],f[N],cnta;
//树剖数组，top链顶，id[u]为u在序列中的下表，son重儿子，d深度，f为父亲 
int col[N];//每个点颜色 
int pos1[N],pos2[N];
//pos1[i],pos2[i]为颜色为i的两个点的编号 
int sum[N];
//原树内以u为根的子树内的颜色个数
int root;
//新树根节点 
bool del[N];//该点是否删去
vector<int> ans;//存答案 
struct edge
{
	int v,nxt;
}a[N<<1];//链式前向星建图 
void add(int u,int v) 
{
	a[++cnt].v=v;
	a[cnt].nxt=head[u];
	head[u]=cnt;
}
struct seg
{
	bool assign,val;//区间赋值，单点查询线段树
	//assign为lazy标记，val为值 
}s[N<<2];
int read()//快读 
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
void pushdown(int rt)//下传 
{
	if(s[rt].assign)
	{
		s[rt<<1].assign|=1;
		s[rt<<1|1].assign|=1;
		s[rt<<1].val|=1;
		s[rt<<1|1].val|=1;
		s[rt].assign=0;
	}
}
void update(int l,int r,int rt,int L,int R)
{//区间加 
	if(L<=l&&R>=r)
	{
		s[rt].val|=1;
		s[rt].assign|=1;
		return;
	}
	pushdown(rt);
	int mid=(l+r)>>1;
	if(L<=mid) update(l,mid,rt<<1,L,R);
	if(R>mid) update(mid+1,r,rt<<1|1,L,R);
}
int query(int l,int r,int rt,int pos)
{//单点查询 
	if(l==r) return s[rt].val;
	int mid=(l+r)>>1;
	pushdown(rt);
	if(pos<=mid) return query(l,mid,rt<<1,pos);
	return query(mid+1,r,rt<<1|1,pos);
}
void dfs(int u,int fa)
{//预处理深度，子树大小，重儿子 
	d[u]=d[fa]+1,sz[u]=1,f[u]=fa;
	for(int i=head[u];i!=0;i=a[i].nxt)
	{
		int v=a[i].v;
		if(v==fa||del[v]) continue;
		dfs(v,u);
		sz[u]+=sz[v];
		if(sz[v]>sz[son[u]]) son[u]=v;
	}
}
void dfs2(int u,int t)
{//预处理链顶，在序列中的下标 
	top[u]=t,id[u]=++cnta;
	if(!son[u]) return;
	dfs2(son[u],t);
	for(int i=head[u];i!=0;i=a[i].nxt)
	{
		int v=a[i].v;
		if(v==f[u]||v==son[u]||del[v]) continue;
		dfs2(v,v); 
	}
}
int lca(int u,int v)
{//树剖求LCA 
	while(top[u]!=top[v])
	{
		if(d[top[u]]>d[top[v]]) swap(u,v);
		v=f[top[v]];
	}
	if(d[u]>d[v]) swap(u,v);
	return u;
}
void path_update(int u,int v)
{//树剖对路径进行赋值 
	while(top[u]!=top[v])
	{
		if(d[top[u]]>d[top[v]]) swap(u,v);
		update(1,n,1,id[top[v]],id[v]);
		v=f[top[v]];
	}
	if(d[u]>d[v]) swap(u,v);
	update(1,n,1,id[u],id[v]);
}
void get_sum(int u,int fa)//统计差分数组 
{
	for(int i=head[u];i!=0;i=a[i].nxt)
	{
		int v=a[i].v;
		if(v==fa) continue;
		get_sum(v,u);
		sum[u]+=sum[v];
	}
}
void assign(int u,int fa,int end)//在原树上删点 
{//删去原树除去 以end为根的子树 的所有点 
	del[u]=1;
	for(int i=head[u];i!=0;i=a[i].nxt)
	{
		int v=a[i].v;
		if(v==end||v==fa) continue;
		assign(v,u,end);
	}
}
bool check(int u)//判断是否删掉2n这个点 
{
	for(int i=head[u];i!=0;i=a[i].nxt)
	{
		int v=a[i].v;
		if(v==f[u]) continue;
		if(sz[v]>=n/2)
		{//判断其儿子的子树是否合法 
			if(sum[v]==n/2) 
			{
				assign(n,0,v);//删点 
				return true;
			}
			return false;
		}
	}
	return false;
}
void modify(int u,int fa)//新树上删点 
{
	int pos=0;
	if(pos1[col[u]]==u) pos=pos2[col[u]];
	else pos=pos1[col[u]];
	path_update(root,pos);//更新另一个点 
	del[u]=1;
	for(int i=head[u];i!=0;i=a[i].nxt)
	{
		int v=a[i].v;
		if(v==fa||del[v]) continue;
		modify(v,u);
	}
}
int main()
{
	n=read()*2;
	for(int i=1;i<=n;i++) 
	{
		col[i]=read();
		if(pos1[col[i]]) pos2[col[i]]=i;
		else pos1[col[i]]=i;
	}
	for(int i=1;i<n;i++)
	{
		int u=read(),v=read();
		add(u,v),add(v,u);
	}
	dfs(n,0);//以2n这个点为根 
	dfs2(n,0);
	for(int i=1;i<=n;i++)
	{
		int l=lca(pos1[i],pos2[i]);
		sum[pos1[i]]++,sum[pos2[i]]++,sum[l]--;
	}
	get_sum(n,0);
	if(check(n))//如果可以删2n这个点 
	{
		if(pos1[col[n]]==n) root=pos2[col[n]];
		else root=pos1[col[n]];
		cnta=0;
		memset(son,0,sizeof(son));
		dfs(root,0);//以root为根重构一下树 
		dfs2(root,0);
	}
	else root=n;//树根没变，可以不用重构 
	for(int i=1,l;i<=n;i++)
	{
		if(del[pos1[i]]) l=pos2[i];//如果只有一个该颜色的点未删，则它的祖先都不能删 
		else if(del[pos2[i]]) l=pos1[i];
		else l=lca(pos1[i],pos2[i]);//如果有两个同颜色的节点未被删，则它们的公共祖先都不能删 
		//更新哪些节点不能删 
		path_update(root,l);
	}
	for(int u=n;u>=1;u--)
	{
		if(del[u]) continue;//已经被删过 
		if(!query(1,n,1,id[u])) modify(u,f[u]);//如果能删 
		else ans.push_back(u);
	}
	printf("%d\n",ans.size());
	for(int i=ans.size()-1;i>=0;i--) printf("%d ",ans[i]);
	return 0;
}

（制作不易，若有错误请指出，如果对您有帮助，可以点个赞么，谢谢！）