2-SAT 简记

2-SAT 为一串的布尔变量，需要求我们求出一组解以满足所有布尔方程或报告无解。

先根据所有条件连边。\(如果a，则一定有b\)，则可以连边 \(a\to b\)。

注意，这里的边类似差分约束的边，是必须满足 所有边 的要求，而非选择一些边来满足要求。若 \(a\) 成立，则一定有 \(b\)。

判断无解

然后我们发现如果一些边和点构成强连通分量，则当其中一个成立时，该强连通分量内所有点都成立。

也就是说，如果 \(a_i=0\) 和 \(a_i=1\) 在同一强连通分量内时，因为两个当中必有一个成立，所以就会导致出一个情况就是 \(a_i=0且1\) ，明显是无解的。

所以当两个对立条件并且其中有且仅有一个成立时，若他们在同一连通分量内，则无解。

构造可行解

如果随意构造，可能出现一下情况：

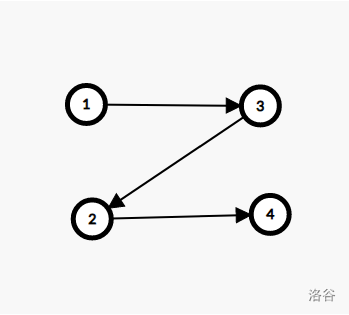
\(1\) 代表 \(a=0\)，\(3\) 代表 \(a=1\)，\(2\) 代表 \(b=0\)，\(4\) 代表 \(b=1\)。

如果我们令 \(a=0\)，那么会导致 \(a=1且0\)，不合法。所以我们按照拓扑序，将该变量赋值为拓扑序小的一方。

如果用 Tarjan 则缩点顺序为拓扑序的倒序，所以就赋值为缩点顺序大的一方。

CF1903F Babysitting

可以发现每一个点都有两种状态：选或不选。这就启发我们，可不可以用2-SAT来解决这个问题。

设 \(i\)为选第 \(i\) 个点， \(i+n\) 为不选第 \(i\) 个点。

最小点覆盖就是一个点集使得任意一条边的两个端点中至少有一个在点集内。那么对应如果不选 \(u\) 则必选 \(v\)，反之亦然。则有边 \((u+n,v)\)，\((v+n,u)\) 。

然后想要最小值最大，则考虑二分答案。

设当前值为 \(mid\)，那么如果选了 \(u\)，则 \([u-mid+1,u+mid-1]\) 的点都不能选，则有边 \((u,x)\) ，\(x\in[u-mid+1,u+mid-1]\)。

但是会发现这是区间连边啊，直接连可能回到 \(n^2\) 级别的啊，怎么开的下？

向区间连边，可以想到线段树优化建图。所以建一棵线段树，然后每个点向其两个儿子连有向边。然后进行区间连边。

所以就出来了，二分答案 \(mid\)，每一次重新建边并跑Tarjan进行判断是否有解就行了，找到最大的 \(mid\) 使得有解。

时间复杂度 \(O(n\log^2 n)\)。

提交记录