差分约束学习笔记

差分约束用来解决这一类问题：

有 $n $ 个形如 $a_x-a_y\le k$ 的二元一次不等式，求出一组合法解满足所有不等式，或报告无解。

可以发现这个等式有点像最短路中的 $dis_v\le dis_u+w$ 式子，所以可以类比最短路问题。如果我们把上式用图建出来，再跑最短路会怎么样？

先转化一下式子，变为 $a_x\le a_y+k$ ，即为边 $( y , x , k )$ ，（这里$ (u,v,w)$ 表示$u$ 为起点，$v$ 为终点，$w$ 为边权的有向边）。那么如果存在最短路，则对于上述的所有条件都一定满足，这里可以想一想。

但是序列中有些点可能并没有被限制，或者说可能建出的图并不是一个连通块，所以考虑建一个超级源点 $0$ ，向所有点建一条边权为 $0$ 的有向边。这样就能保证从 $0$ 号点出发能到达所有点了。

但是如果不存在最短路呢？不存在最短路，也就是建出的图中存在负环。举个例子：

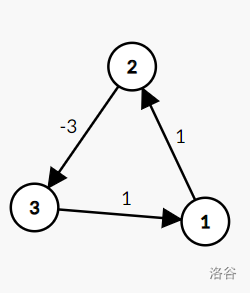
此时图中存在负环，那么对应回不等式中即 $\begin{cases}a_2\le a_1+1\\a_3\le a_2-3\\a_1\le a_3+1\end{cases}$ ，带入 $1$ 式到 $2$ 式得到 $a_3\le a_1-2$，再带入该式到 $3$ 式得$a_1\le a_1-1$，明显无解。可以自己手造一些例子找找规律，理解一下。

所以图中存在负环，则不等式无解，否则我们可以通过最短路来构造出一组解来。

但是最短路中的每一个解都一定小于等于 $0$，因为超级源点到每一个点的边的边权为 $0$。如果想求非负整数解，就将所有数减去所有数中的最小值，这样就是非负的了。因为同增同减，相对大小不变，还是满足所有不等式。

那么除了最短路，我们可不可以同样地跑最长路呢？

说干就干，最长路的不等式为 $dis_u+w\le dis_v$，所以将上式转化为 $a_x-k\le a_y$，则为边 $(x,y,-k)$。同样，如果存在正环则无解，最后我们跑最长路同样可以得到一组解。

那么，用最短路跑出的解与最长路跑出的解有什么区别呢？

首先考虑最短路，有式子 $dis_v\le dis_u+w$ ，则此处的 $dis_v$ 一定取的是最大的值使得满足所有要求，所以可以理解为最短路求得是最大解。

设 $x=\min_{u\in pre_v} (dis_u+w)$，则当 $dis_v\le x$ 时所有不等式成立，而按照最短路算法，我们最终会取 $dis_v$ 为 $x$，所以为最大解。

然后就是最长路，同理，有式子 $dis_v\ge dis_u+w$ ，则此处的 $dis_v$ 一定取的是最小的值使得满足所有要求，所以可以理解为最长路求得是最小解。

所以结论是：求最大解跑最短路，求最小解跑最长路。

接下来为例题（如需看题面请点击题目）：

1. P2868 [USACO07DEC] Sightseeing Cows G

求一张图上的一个环使得环上点权和与边权和的比值最大。

注：本题不是差分约束

这类和的比值最大/小的问题不难想到0/1分数规划，二分这个比值 $x$，则转化一下式子：

\[\frac{\sum F_u}{\sum T_e}\ge x \ \ \ \to\ \ \ \sum F_u\ge x\times \sum T_e \ \ \ \to\ \ \ \sum F_u-x\times \sum T_e\ge 0 \]

也就是说我们需要找到一个环使得 $点权-x\times 边权$ 的值不小于 $0 $，如果我们把左右两端同时乘上 $-1$，则有 $x\times \sum T_e-\sum F_u\le 0$，有点类似一个判负环的操作。但是还需要找有没有 $0$ 环，有点麻烦。

如果我们不管 $0$ 环，直接求负环从而得出的答案是否对呢？题目说四舍五入到两位，所以如果我们把精度开高一点，这样 $|最终答案-我们求出的答案|<10^{-2}$，就一定对。因为 $0$ 环只会在某几个特定值存在，而非一段连续的值，所以误差会非常小，足以通过本题。

所以最终思路为二分答案，然后对所有边进行重新赋值边权（ $w\to x\times w$ ）和点权（ $w\to -w$ ），然后跑spfa最短路来判断负环。

时间复杂度 $O(nm\log V)$，$V$为 $\frac{值域}{我们控制的精度}$，值域不会超过 $5\times 10^6$，精度大概控制在 $10^{-4}$ 左右即可通过本题。

代码：

#include<bits/stdc++.h>
#include<cstring>
using namespace std;
#define int long long
const int N=1e5+5;
const double eps=1e-4;
int head[N<<1],n,cnt,m,cnta[N],w[N];
double dis[N];
bool vis[N];
struct edge
{
	int v,nxt;
	double w;
}a[N<<1];
void add(int u,int v,double w)
{
	a[++cnt].v=v;
	a[cnt].w=w;
	a[cnt].nxt=head[u];
	head[u]=cnt;
}
int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
bool spfa(int s)
{
	for(int i=0;i<=n;i++) dis[i]=1e9,vis[i]=0,cnta[i]=0;
	queue<int> q;
	q.push(s);
	vis[s]=1;
	cnta[s]=1;
	dis[s]=0;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(int i=head[u];i!=0;i=a[i].nxt)
		{
			int v=a[i].v;
			if(dis[v]-dis[u]-a[i].w-w[v]>=eps)
			{
				dis[v]=dis[u]+a[i].w+w[v];
				if(!vis[v])
				{
					vis[v]=1;
					q.push(v);
					if(++cnta[v]==n+1) return true;
				}
			}
		}
	}
	return false;
}
bool check(double mid)
{
	for(int i=1;i<=cnt;i++) a[i].w*=mid;
	bool ans=spfa(0);
	for(int i=1;i<=cnt;i++) a[i].w/=mid;
	return ans;
}
signed main()
{
	n=read(),m=read();
	for(int i=1;i<=n;i++) w[i]=-read();
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read(),w=read();
		add(u,v,w);
	}
	for(int i=1;i<=n;i++) add(0,i,0);
	double l=0.0,r=1e7,ans=0.0;
	while(r-l>eps)
	{
		double mid=(l+r)/2;
		if(check(mid)) ans=mid,l=mid;
		else r=mid;
	}
	printf("%.2f",ans);
	return 0;
}

2. SPOJ INTERVAL-Interval

差分约束经典题。

如果我们记 $f_i$ 为 $[1,i]$ 中选了的个数，则限制 $\{a_i,b_i,c_i\}$，则可表示为 $f_{b_i}-f_{a_i-1}\ge c_i$，我们求最小值就跑最长路，转化一下式子为 $f_{b_i}\ge f_{a_i-1}+c_i$，即为边 $(a_i-1,b_i,c_i)$。

但是每一个数最多被取一次，且前缀和数组是单调不降的，所以还有隐藏的两个式子：$\begin{cases}f_i-f_{i-1}\ge 0\\ f_i-f_{i-1}\le 1\end{cases}$ 。即为边 $(i-1,i,0)$ 和 $(i,i-1,-1)$。

然后建一个超级源点跑最长路即可。答案为 $dis_{\max b_i}$。

时间复杂度 $O(nV)$

然后跑得比较快？spfa能过？反正挺玄学的，我也不会证。

代码：

#include<bits/stdc++.h>
#include<cstring>
using namespace std;
const int N=1e6+5;
int head[N<<1],n,m,dis[N],cnt,s,vis[N];
struct edge{int v,nxt,w;}a[N<<2];
void add(int u,int v,int w){a[++cnt].v=v,a[cnt].w=w;a[cnt].nxt=head[u];head[u]=cnt;}
int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
void spfa(int s)
{
	queue<int> q;
	q.push(s);
	dis[s]=0;
	vis[s]=1;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(int i=head[u];i!=0;i=a[i].nxt)
		{
			int v=a[i].v;
			if(dis[v]<dis[u]+a[i].w)
			{
				dis[v]=dis[u]+a[i].w;
				if(!vis[v])
				{
					vis[v]=1;
					q.push(v);
				}
			}
		}
	}
}
signed main()
{
	int t=read();
	while(t--)
	{
		m=read();
		memset(dis,-0x3f3f3f3f,sizeof(dis));
		memset(head,0,sizeof(head));
		cnt=0;
		int maxn=0;
		for(int i=1,u,v,w;i<=m;i++)
		{
			u=read()+1,v=read()+1,w=read();
			maxn=max(maxn,v);
			add(u-1,v,w);
		}
		s=maxn+1;
		for(int i=1;i<=maxn;i++) add(i-1,i,0),add(i,i-1,-1);
		for(int i=0;i<=maxn;i++) add(s,i,0);
		spfa(s);
		printf("%d\n",dis[maxn]);
	}
	return 0;
}

3. P4878 [USACO05DEC] Layout G

求最大解跑最短路，对于条件 $a_u-a_v\le k$ 转化为 $a_u\le a_v+k$，建边 $(v,u,k)$。对于条件 $a_u-a_v\ge k$ 转化为 $a_u-k\le a_v$，建边 $(u,v,-k)$。

然后以超级源点为起点跑最短路判断负环。但是以超级源点为起点跑最短路是钦定 $a_0=0$ 的最大解，而我们想求 $a_n-a_1$ 的最大解，所以从 $1$ 点开始再跑一遍最短路，答案为 $dis_n$。

时间复杂度 $O(nm)$。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int head[N<<1],cnt,s,n,m1,m2,dis[N],cnta[N];
bool vis[N];
struct edge
{
	int v,nxt,w;
}a[N<<1];
void add(int u,int v,int w)
{
	a[++cnt].v=v;
	a[cnt].w=w;
	a[cnt].nxt=head[u];
	head[u]=cnt;
}
int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
void spfa(int s)
{
	memset(dis,0x3f3f3f3f,sizeof(dis));
	queue<int> q;
	q.push(s);
	dis[s]=0;
	cnta[s]=1;
	vis[s]=1;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(int i=head[u];i!=0;i=a[i].nxt)
		{
			int v=a[i].v;
			if(dis[v]>dis[u]+a[i].w)
			{
				dis[v]=dis[u]+a[i].w;
				if(!vis[v])
				{
					cnta[v]++;
					vis[v]=1;
					q.push(v);
					if(cnta[v]==n+1) printf("-1"),exit(0);
				}
			}
		}
	}
}
int main()
{
	n=read(),m1=read(),m2=read();
	for(int i=1;i<=m1;i++)
	{
		int u=read(),v=read(),w=read();
		add(u,v,w);
	}
	for(int i=1;i<=m2;i++)
	{
		int u=read(),v=read(),w=read();
		add(v,u,-w);
	}
	s=0;
	for(int i=1;i<=n;i++) add(s,i,0);
	for(int i=2;i<=n;i++) add(i,i-1,0);
	spfa(s);
	spfa(1);
	if(dis[n]>=0x3f3f3f3f) puts("-2"),exit(0);
	cout<<dis[n];
	return 0;
}

4. CF803E Roma and Poker

好像dp能做。但是还是用差分约束吧。

设 $f_i$ 为 $[1,i]$ 中W的数量与L的数量之差。

因为是求一组可行解，所以跑最长路最短路皆可。这里我用的最短路。

首先对于出现次数差 $<k$，可以建立不等式 $-k<f_i-f_0 <k$，差分约束要求小于等于号或大于等于号，所以转化为 $-k+1\le f_i-f_0 \le k-1$则为边 $(0,i,k-1)$ 和 $(i,0,k-1)$$（i\neq n）$。

然后对于最终的出现次数差的绝对值为 $k$，则有 $f_n-f_0=k$ 或 $f_n-f_0=-k$ ，但是差分约束求的是所有要求皆满足而非其中一个被满足，所以这里进行分类讨论，分别枚举 $f_n-f_0$ 的大小为 $k$ 还是 $-k$ 。

再对于原串进行建边。

如果 $s_i=L$，则有 $-1\le f_i-f_{i-1}\le -1$，则有边 $(i,i-1,1)$ 和 $(i-1,i,-1)$。
如果 $s_i=W$，则有 $1\le f_i-f_{i-1}\le 1$，则有边 $(i,i-1,-1)$ 和 $(i-1,i,1)$。
如果 $s_i=?$，则有 $-1\le f_i-f_{i-1}\le 1$ ,则有边 $(i,i-1,1)$ 和 $(i-1,i,1)$。

跑一遍spfa即可。

时间复杂度 $O(n^2)$。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+5;
int head[N<<1],k,cnt,n,m,dis[N],cnta[N];
bool vis[N];
char e[N];
struct edge
{
	int v,nxt,w;
}a[N<<1];
void add(int u,int v,int w)
{
	a[++cnt].v=v;
	a[cnt].w=w;
	a[cnt].nxt=head[u];
	head[u]=cnt;
}
int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
bool spfa(int s)
{
	memset(dis,0x3f3f3f3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	memset(cnta,0,sizeof(cnta));
	queue<int> q;
	dis[s]=0;
	vis[s]=1;
	cnta[s]=1;
	q.push(s);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(int i=head[u];i!=0;i=a[i].nxt)
		{
			int v=a[i].v;
			if(dis[v]>dis[u]+a[i].w)
			{
				dis[v]=dis[u]+a[i].w;
				if(!vis[v])
				{
					vis[v]=1;
					q.push(v);
					if(++cnta[v]==n+2) return false;
				}
			}
		}
	}
	return true;
}
void ad(int u,int v,int l,int r)
{
	add(u,v,-l);
	add(v,u,r);
}
void print()
{
	for(int i=1;i<=n;i++) 
	{
		if(dis[i]>dis[i-1]) putchar('W');
		else if(dis[i]<dis[i-1]) putchar('L');
		else putchar('D');
	}
}
int main()
{
	n=read(),k=read();
	int s=n+1;
	for(int i=1;i<=n;i++) cin>>e[i];
	for(int i=1;i<=n;i++)
	{
		if(i!=n) ad(i,0,1-k,k-1);
		if(e[i]=='?') ad(i,i-1,-1,1);
		else if(e[i]=='L') ad(i,i-1,-1,-1);
		else if(e[i]=='W')ad(i,i-1,1,1);
		else ad(i,i-1,0,0);
	}
	ad(n,0,-k,-k);
	for(int i=0;i<=n;i++) add(s,i,0);
	if(spfa(s)) print(),exit(0);
	memset(head,0,sizeof(head));
	cnt=0;
	for(int i=1;i<=n;i++)
	{
		if(i!=n) ad(i,0,1-k,k-1);
		if(e[i]=='?') ad(i,i-1,-1,1);
		else if(e[i]=='L') ad(i,i-1,-1,-1);
		else if(e[i]=='W')ad(i,i-1,1,1);
		else ad(i,i-1,0,0);
	}
	ad(n,0,k,k);
	for(int i=0;i<=n;i++) add(s,i,0);
	if(spfa(s)) print(),exit(0);
	puts("NO");
	return 0;
}

5. CF241E Flights

从 $1$ 出发到达 $n$ 的所有路径长度相等，实际上就是从 $1$ 出发到达所有点的所有路径长度相等。

构造可行解，这里选择跑最短路。

因为我们可以先选择一些点使其边权从 $1$ 变为 $2$，也就是说如果原图有边 $(u,v)$，则有条件 $1\le dis_v-dis_u\le 2$ 。所以有边 $(u,v,2)$ 和 $(v,u,-1)$。

好像就完了？

但是会发现我们在一些原本有解的情况输出了无解。

实际上最初的结论有一点问题。如果有一些点无法满足要求但是 $1$ 到 $n$ 的所有路径都不经过它则仍然有解。但是跑差分约束时把它判为无解了。

所以还需从 $1$ 出发标记所有能到的点，再建反向图，从 $n$ 出发标记所有能到的点。如果该点既能从 $1$ 到，又能从 $n$ 到，则该点必须满足要求。因为是DAG，所以这样做是对的。

然后就可以跑差分约束。

时间复杂度 $O(nm)$。

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+5;
int head[N<<1],cnt,n,m,dis[N],cnta[N],u[N],v[N];
bool vis[N],b[N],b2[N];
struct edge
{
	int v,nxt,w;
}a[N<<1];
void add(int u,int v,int w)
{
	a[++cnt].v=v;
	a[cnt].w=w;
	a[cnt].nxt=head[u];
	head[u]=cnt;
}
int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
void spfa(int s)
{
	queue<int>q;
	q.push(s);
	memset(dis,0x3f3f3f3f,sizeof(dis));
	dis[s]=0;
	vis[s]=1;
	cnta[s]=1;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(int i=head[u];i!=0;i=a[i].nxt)
		{
			int v=a[i].v;
			if(dis[v]>dis[u]+a[i].w)
			{
				dis[v]=dis[u]+a[i].w;
				if(!vis[v])
				{
					vis[v]=1;
					q.push(v);
					if(++cnta[v]==n+2) puts("No"),exit(0);
				}
			}
		}
	}
}
void ad(int u,int v,int l,int r)
{
	add(v,u,-l);
	add(u,v,r);
}
void dfs(int u)
{
	for(int i=head[u];i!=0;i=a[i].nxt)
	{
		int v=a[i].v;
		if(!b[v]) b[v]=1,dfs(v);
	}
}
void dfs2(int u)
{
	for(int i=head[u];i!=0;i=a[i].nxt)
	{
		int v=a[i].v;
		if(!b2[v]) b2[v]=1,dfs2(v);
	}
}
int main()
{
	n=read(),m=read();
	for(int i=1;i<=m;i++)u[i]=read(),v[i]=read(),add(v[i],u[i],1);
	b[n]=1;
	dfs(n);
	memset(head,0,sizeof(head));
	cnt=0;
	for(int i=1;i<=m;i++) add(u[i],v[i],1);
	b2[1]=1;
	dfs2(1);
	for(int i=1;i<=n;i++) b[i]&=b2[i];
	memset(head,0,sizeof(head));
	cnt=0;
	int s=0;
	for(int i=1;i<=m;i++) if(b[u[i]]&&b[v[i]])ad(u[i],v[i],1,2);
	for(int i=1;i<=n;i++) add(s,i,0);
	spfa(s);
	puts("Yes");
	for(int i=1;i<=m;i++) 
	{
		if(!b[u[i]]||!b[v[i]]) printf("1\n");
		else printf("%d\n",abs(dis[u[i]]-dis[v[i]]));
	}
	return 0;
}

6. CF1450E Capitalism

这里想求最大值，则用最短路。

根据题意，如果 $ a_j-a_i=1$，则转化为 $1\le a_j-a_i\le 1$，则有边 $(i,j,1)$ 和 $(j,i,-1)$。但是还有一种，是 $a_j-a_i=1或-1$，$a_j-a_i$ 的范围不再是一整段，而是两段了。该怎么处理？

会发现在求最小解时，我们能通过 $-1$ 边更新则用 $-1$ 边更新，也就是说两个点之间的奇偶性一定不同。也就是说，如果可以，一定不会出现 $a_i=a_j$ 的情况。那么什么情况下会出现 $a_i=a_j$ 的情况呢？就是存在奇环的时候会导致两点奇偶性相同，此时无解。

所以我们可以直接连 $-1\le a_j-a_i \le 1$对应的 $(j,i,1)$ 和 $(i,j,1)$ 就行了，然后判断是否有负环，如果有负环则无解。

然后是答案的问题，我们在判断负环时跑的最短路是基于超级源点为 $0$ 的条件下的最大解。但是事实上，这可能并不是除 $0$ 号点外所有点极差的最大值，所以还需枚举所有点，然后以改点为源点跑一遍最短路，则答案为每一次所有点距离的最大值。

时间复杂度 $O(n^2m)$。

好像可以跑floyd，是 $O(n^3)$的，会更快，但是，懒得改了。

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+5;
int head[N<<1],cnta[N],dis[N],cnt,n,m,ans[N],col[N];
bool vis[N];
struct edge
{
	int v,nxt,w;
}a[N<<1];
void add(int u,int v,int w)
{
	a[++cnt].v=v;
	a[cnt].w=w;
	a[cnt].nxt=head[u];
	head[u]=cnt;
}
int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
void spfa(int s)
{
	queue<int> q;
	memset(dis,0x3f3f3f3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	memset(cnta,0,sizeof(cnta));
	vis[s]=1;
	q.push(s);
	cnta[s]=1;
	dis[s]=0;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(int i=head[u];i!=0;i=a[i].nxt)
		{
			int v=a[i].v;
			if(dis[v]>dis[u]+a[i].w)
			{
				dis[v]=dis[u]+a[i].w;
				if(!vis[v])
				{
					vis[v]=1;
					q.push(v);
					if(++cnta[v]==n+1) puts("NO"),exit(0);
				}
			}
		}
	}
}
void ad(int u,int v,int l,int r)
{
	add(v,u,-l);
	add(u,v,r);
}
bool dfs(int u)
{
	for(int i=head[u];i!=0;i=a[i].nxt)
	{
		int v=a[i].v;
		if(col[v]&&col[v]!=col[u]^1) return true;
		if(!col[v])
		{
			col[v]=col[u]^1;
			if(dfs(v)) return true;
		}
	}
	return false;
}
int main()
{
	n=read(),m=read();
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read(),w=read();
		if(w==0) ad(u,v,-1,1);
		else ad(u,v,1,1);
	}
	col[1]=2;
	if(dfs(1)) printf("NO"),exit(0);
	int s=0;
	for(int i=1;i<=n;i++) add(s,i,0);
	spfa(s);
	int maxn=0;
	for(int i=1;i<=n;i++)
	{
		spfa(i);
		int res=0;
		for(int i=1;i<=n;i++) res=max(res,dis[i]);
		if(res>maxn)
		{
			for(int i=1;i<=n;i++) ans[i]=dis[i];
			maxn=res;
		}
	}
	printf("YES\n");
	printf("%d\n",maxn);
	for(int i=1;i<=n;i++) printf("%d ",ans[i]);
	return 0;
}

7. P4926 倍杀测量者

首先，正难则反，考虑找到最小的 $T$ 使得没人女装，最终答案则为我们求出的 $T-$无穷小。同样，因为有 $10^{-4}$ 的误差可以被接受，所以当我们的精度足够大时，最终答案与 $T$ 的差值一定 $<10^{-4}$，也就是说，我们求出的 $T$，与正确答案近似相等，误差在可接受范围内，直接输出我们求出的 $T$ 可以过。

现在考虑如果找到这样一个 $T$。

首先对于第一类，他不女装当且仅当 $f_u\ge (k-T)f_v$。
对于第二类，他不女装当且仅当 $f_u(k-T)> f_v$。

会发现这是一个乘法啊，如果他是一个加法，那就可以直接跑差分约束了啊。

那么怎么转化为加法呢？

有一个常用的Trick：通过转化为对数使得乘法变为加法。

因为我们知道 $a>b\times c$，则根据函数 $f(x)=\log_2x$ 的单调性可知 $\log_2a>\log_2(b\times c)$，又根据对数的运算法则有：$\log_2(b\times c)=\log_2b+\log_2c$，所以则有 $\log_2a>\log_2b+\log_2c$，就变成了加法。

所以对于以上式子，则有如下转化：

对于第一类，他不女装当且仅当 $\log_2f_u\ge \log_2(k-T)+\log_2f_v$。
对于第二类，他不女装当且仅当 $\log_2f_u+\log_2(k-T)> \log_2f_v$。

然后下面那个式子是小于号，我们想要 $\ge$ 号，所以在右边加上无穷小，则有 $\log_2f_u+\log_2(k-T)>\log_2f_v+eps$。此处 $eps$ 为我们控制的精度大小，可以理解为无穷小。

这里选择跑最长路，然后记 $dis_u=\log_2f_u$，对于第一种情况，有边 $(v,u,\log2(k-T))$；对于第二种情况有边 $(v,u,-\log_2(k-T))$。

然后题目对于一些位置已经确定了值，设为 $a_i$，则有条件 $a_i\le f_u-f_0\le a_i$，转化一下，则有边 $(u,0,-\log_2a_i)$和边 $(0,u,\log_2a_i)$。然后对于没有确定值的位置，连接 $(0,i,0)$。

如果有解，则无人女装。所以判断是否有正环即可。

也就是二分后建图加判正环。

时间复杂度 $O(nm\log V)$。

洛谷讨论区里的hack主要是卡的前面的式子里 $>$ 转 $\ge$ 的操作。测试点里没卡这个。

代码：

#include<bits/stdc++.h>
#include<cstring>
using namespace std;
#define int long long
const int N=2e5+5;
const double eps=1e-7;
int head[N<<1],n,m,q,cnt,p[N];
int cnta[N];
bool vis[N];
double dis[N];
struct edge
{
	int v,nxt,type;
	double w;
}a[N<<1];
void add(int u,int v,double w,int f)
{
	a[++cnt].v=v;
	a[cnt].w=w;
	a[cnt].type=f;
	a[cnt].nxt=head[u];
	head[u]=cnt;
}
int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
bool spfa(int s,double T)
{
	for(int i=0;i<=n;i++) dis[i]=-1e9,cnta[i]=0,vis[i]=0;
	dis[s]=0.0;
	queue<int> q;
	q.push(s);
	vis[s]=1;
	cnta[s]=1;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(int i=head[u];i!=0;i=a[i].nxt)
		{
			int v=a[i].v;
			double w;
			if(a[i].type==3) w=a[i].w;
			else if(a[i].type==1) w=log2(a[i].w-T);
			else w=-log2(a[i].w+T)+eps;//加无穷小转>=
			if(eps<dis[u]+w-dis[v])
			{
				dis[v]=dis[u]+w;
				if(!vis[v])
				{
					vis[v]=1;
					q.push(v);
					if(++cnta[v]==n+2) return false;
				}
			}
		}
	}
	return true;
}
signed main()
{
	n=read(),m=read(),q=read();
	double l=0.0,r=1e9,ans=0.0;
	int minn=1e9;
	for(int i=1;i<=m;i++)
	{
		int op=read(),u=read(),v=read(),k=read();
		if(op==1) add(v,u,k,1),minn=min(minn,k);
		else add(v,u,k,2);
	}
	r=minn-eps;
	for(int i=1;i<=q;i++)
	{
		int x=read(),w=read();
		p[x]=w;
		add(0,x,log2(w),3);
		add(x,0,-log2(w),3);
	}
	for(int i=1;i<=n;i++) 
	{
		if(!p[i]) add(0,i,-1e7,3);
	}
	if(spfa(0,0)) printf("-1"),exit(0);
	while(eps<r-l)
	{
		double mid=(l+r)/2;
		if(spfa(0,mid)) r=mid-eps,ans=mid;
		else l=mid+eps;
	}
	printf("%.6f",ans);
	return 0;
}

8. P3275 [SCOI2011] 糖果

求最小解跑最长路。

$X=1$，对应 $f_u=f_v$，即 $0\le f_u-f_v\le 0$，为边 $(u,v,0)$ 和 $(v,u,0)$ 。
$X=2$，对应 $f_u<f_v$，即 $f_u-f_v\le -1$，为边 $(u,v,1)$。
$X=3$，对应 $f_u\ge f_v$，即 $0\le f_u-f_v$，为边 $(v,u,0)$ 。
$X=4$，对应 $f_u>f_v$，即 $1\le f_u-f_v$，为边 $(v,u,1)$ 。
$X=5$，对应 $f_u\le f_v$，即 $f_u-f_v\le 0$，为边 $(u,v,0)$ 。

如果有正环则无解。

但是 $n\le10^5$，直接跑 spfa 绝对会被卡。

所以考虑找找性质，会发现所有边的边权非负！这个性质挺好的，因为它告诉我们所有环都是边权和为 $0$ 的环。因为一旦有 $1$ 边出现在环里，则该环就变成了正环，直接无解。

所以每一个环内的所有 $f$ 值都相等，因为是从 $0$ 边扩展来的。

那么可以考虑用强连通分量缩点。这样缩下来后一定是一个DAG，因为如果存在环的话还可以再缩，不满足强连通分量的定义。现在我们需要对DAG中每一个点求出最长路，直接拓扑排序。

然后判正环就判是否存在一个强连通分量使得该强连通分量内所有边边权之和大于 $0$。

时间复杂度 $O(n)$。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+5;
int head[N<<1],cnt,n,m,dis[N],val[N];

int dfn[N],low[N],cnta,tmp,id[N],st[N],top;

int uu[N],vv[N],ww[N],ru[N],idx;

bool b[N];
struct edge
{
	int v,nxt,w;
}a[N<<1];
void add(int u,int v,int w,bool f)
{
	if(f) uu[++idx]=u,vv[idx]=v,ww[idx]=w;
	a[++cnt].v=v;
	a[cnt].w=w;
	a[cnt].nxt=head[u];
	head[u]=cnt;
}
int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
void tarjan(int u)
{
	dfn[u]=low[u]=++cnta;
	st[++top]=u;
	b[u]=1;
	for(int i=head[u];i!=0;i=a[i].nxt)
	{
		int v=a[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(b[v]) low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		tmp++;
		while(st[top+1]!=u)
		{
			id[st[top]]=tmp;
			b[st[top]]=0;
			top--;
		}
	}
}
void topsort()
{
	queue<int> q;
	for(int i=1;i<=tmp;i++) if(!ru[i]) q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=head[u];i!=0;i=a[i].nxt)
		{
			int v=a[i].v;
			ru[v]--;
			dis[v]=max(dis[v],dis[u]+a[i].w);
			if(!ru[v]) q.push(v);
		}
	}
}
signed main()
{
	n=read(),m=read();
	for(int i=1;i<=m;i++)
	{
		int op=read(),u=read(),v=read();
		if(op==1) add(u,v,0,1),add(v,u,0,1);
		else if(op==2) add(u,v,1,1);
		else if(op==3) add(v,u,0,1);
		else if(op==4) add(v,u,1,1);
		else if(op==5) add(u,v,0,1);
	}
	for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
	memset(head,0,sizeof(head));
	cnt=0;
	for(int i=1;i<=idx;i++) 
	{
		int cu=id[uu[i]],cv=id[vv[i]];
		if(cu!=cv) 
		{
			add(cu,cv,ww[i],0);
			ru[cv]++;
		}
		else val[cu]+=ww[i];
	}
	for(int i=1;i<=tmp;i++) if(val[i]>0) puts("-1"),exit(0);
	topsort();
	int ans=0;
	for(int i=1;i<=n;i++) ans+=dis[id[i]]+1;
	cout<<ans;
	return 0;
}

posted @ 2024-11-05 23:04 Twilight_star 阅读(73) 评论(1) 收藏举报

刷新页面返回顶部

Twilight_star

差分约束 学习笔记