【手撕红黑树 | 史上最详细注解】增删查改 原理剖析 代码实现
1、基本特征
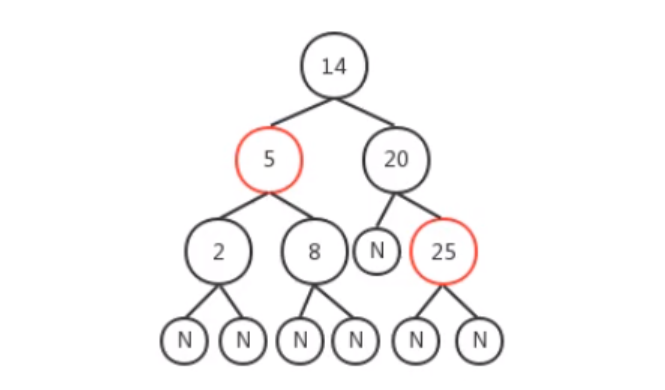
红黑树起源于2-3-4树(或2-3树),底层是二叉查找树,除二叉树的特性外,还有5大特性:
-
根是黑色
-
节点是黑色或红色
-
叶子节点都是黑色
叶子节点为NIL节点,不可忽略,见下图
-
每个红色节点的两个子节点必须是黑色
从每个叶子到根的路径上不能有两个连续的红节点
-
黑色平衡
从任一节点到其所有叶子节点的简单路径上黑色节点数量相同
2、内部节点类Node
双向链表:父 > 子 子 > 父
/**
* 内部节点类
*/
private class Node {
/**
* 键 key
*/
private K key;
/**
* 值 value
*/
private V value;
/**
* 父节点
*/
private Node parent;
/**
* 左子节点
*/
private Node left;
/**
* 右子节点
*/
private Node right;
/**
* 节点颜色
* 红色:true
* 黑色:false
*/
private boolean color;
/**
* 构造器
*
* @param key
* @param value
* @param parent
* @param left
* @param right
*/
public Node(K key, V value, Node parent, Node left, Node right) {
this.key = key;
this.value = value;
this.parent = parent;
this.left = left;
this.right = right;
this.color = BLACK;
}
}
3、成员变量与构造器
/**
* @author 土味儿
* Date 2021/9/10
* @version 1.0
* 红黑树
*/
public class RedBlackTree1<K extends Comparable<K>, V> {
/**
* 根节点
*/
private Node root;
/**
* 元素数量
*/
private int n;
/**
* 红色
*/
private static final boolean RED = true;
/**
* 黑色
*/
private static final boolean BLACK = false;
/**
* 构造器
*/
public RedBlackTree1() {
this.n = 0;
}
}
4、基础方法
4.1、元素数量 size()
public
/**
* 元素数量
*
* @return
*/
public int size() {
return n;
}
4.2、节点颜色 colorOf()
private
/**
* 节点颜色
*
* @param x
* @return
*/
private boolean colorOf(Node x) {
if (x != null) {
return x.color == RED;
}
return BLACK;
}
5、查询
5.1、get()
public
/**
* 得到 key 结点的值
*
* @param key
* @return
*/
public V get(K key) {
Node node = getNode(key);
return node != null ? node.value : null;
}
5.2、getNode()
private
/**
* 获取 key 节点
*
* @param key
* @return
*/
private Node getNode(K key) {
// 空树、空键
if (root == null || key == null) {
return null;
}
// 从根结点开始查找
Node node = root;
// 比较 key 与 h 键的大小
int cmp;
// 循环遍历
while (node != null) {
cmp = key.compareTo(node.key);
if (cmp < 0) {
node = node.left;
} else if (cmp > 0) {
node = node.right;
} else {
return node;
}
}
return null;
}
5.3、树根
public
/**
* 得到树根的value
* @return
*/
public V getRoot(){
return root.value;
}
5.4、最小
-
getMin()
public
/**
* 最小值
* @return
*/
public V getMin() {
Node minNode = getMinNode();
return minNode != null ? minNode.value : null;
}
-
getMinNode()
private
/**
* 最小节点
* 最左侧叶子
*
* @return
*/
private Node getMinNode() {
Node p = root;
if (p != null) {
while (p.left != null) {
p = p.left;
}
}
return p;
}
5.5、最大
-
getMax()
public
/**
* 最大值
*
* @return
*/
public V getMax() {
Node maxNode = getMaxNode();
return maxNode != null ? maxNode.value : null;
}
-
getMaxNode()
private
/**
* 最大节点
* 最右侧叶子
*
* @return
*/
private Node getMaxNode() {
Node p = root;
if (p != null) {
while (p.right != null) {
p = p.right;
}
}
return p;
}
5.6、前驱节点
private
小于当前节点的最大节点
就是当前节点左子树中的最右节点;在左子树中循环向右,最后一个
/**
* 前驱节点
* 小于 t 的最大节点
* t 左子树中最右节点
*
* @param t
* @return
*/
private Node predecessor(Node t) {
// t 为null时,返回null
if (t == null) {
return null;
}
Node p;
// t 有左子树:在左子树中找出最右侧节点即可
if (t.left != null) {
p = t.left;
// 向右循环查找
while (p.right != null) {
p = p.right;
}
return p;
}
// t 没有左子树:向父节点查找
// 在父辈节点中找出最近的左侧节点(t的左侧、最近的父辈节点)
else {
p = t.parent;
Node ch = t;
// 如果父辈在右侧就循环查找
while (p != null && ch == p.left) {
ch = p;
p = p.parent;
}
return p;
}
}
5.7、后继节点
private
大于当前节点的最小节点
就是当前节点右子树中的最左节点;在右子树中循环向左,最后一个
/**
* 后继结点
* 大于 t 的最小值
* t 右子树中最左叶子结点
*
* @param t
* @return
*/
private Node successor(Node t) {
// t 为null时,返回null
if (t == null) {
return null;
}
Node p;
// t 有右子树:在右子树中找出最左侧节点即可
if (t.right != null) {
p = t.right;
// 向左循环查找
while (p.left != null) {
p = p.left;
}
return p;
}
// t 没有右子树:向父节点查找
// 在父辈节点中找出最近的右侧节点(t的右侧、最近的父辈节点)
else {
p = t.parent;
Node ch = t;
// 如果父辈在左侧就循环查找
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
6、修改
public
/**
* 修改
* @param key
* @param value
* @return
*/
public int modify(K key,V value){
// 空树、空键
if (root == null || key == null) {
return 0;
}
// 从根结点开始查找
Node node = root;
// 比较 key 与 h 键的大小
int cmp;
// 循环遍历
while (node != null) {
cmp = key.compareTo(node.key);
if (cmp < 0) {
node = node.left;
} else if (cmp > 0) {
node = node.right;
} else {
node.value = value;
return 1;
}
}
return 0;
}
7、添加
思路:先添加、再调整
新增结点都是红色
都是从叶子节点新增
步骤:
- 空树时,直接添加
- 非空树时,查找要添加位置
public
/**
* 添加
* 当 key 存在时即为修改
* @param key
* @param value
*/
public void put(K key, V value) {
// 空指针
if (key == null) {
throw new NullPointerException();
}
Node t = root;
// 空树
if (t == null) {
// 新建节点
root = new Node(key, value, null, null, null);
// 数量加1
n++;
return;
}
// 非空树,查找插入位置
// 比较值
int cmp;
// 父节点
Node parent;
// 循环查找插入位置
do {
parent = t;
// 比较 key 与 t 节点的键的大小
cmp = key.compareTo(t.key);
// 小于:向左继续查找
if (cmp < 0) {
t = t.left;
}
// 大于:向右继续查找
else if (cmp > 0) {
t = t.right;
}
// 等于:值替换
else {
t.value = value;
// 退出循环,退出
return;
}
} while (t != null);
// 循环正常结束,表示已找到插入位置,就在 parent 的下面,即为 parent 的儿子;此时 t 为null,不能用
Node e = new Node(key, value, parent, null, null);
// 左儿子
if (cmp < 0) {
parent.left = e;
}
// 右儿子
else {
parent.right = e;
}
// 调整
fixAfterPut(e);
// 数量加1
n++;
return;
}
8、添加后调整
8.1、左旋
private
只做旋转,不变色
/**
* 左旋
* -------------------------------------
* P X
* / \\ // \
* a X 左旋后> P c
* / \ / \
* b c a b
* -------------------------------------
* 只做旋转,不做变色
* @param p
*/
private void rotateLeft(Node p) {
// 参数有效性检测
if (p == null || p.right == null) {
return;
}
// 当前节点为 p,它的右子节点为 x
Node x = p.right;
// 左旋后:
// 1、p、x节点的父亲、儿子都发生了变化
// 2、x左子节点的父亲发生变化,儿子不变
// 3、p的父亲的儿子发生变化
// 更新 x 的左子
if(x.left != null){
x.left.parent = p;
}
// 更新 p 的右子
p.right = x.left;
// 更新 x
x.parent = p.parent;
// 更新 p 的父亲
if(p.parent == null){
root = x;
}
else if(p.parent.left == p){
p.parent.left = x;
}
else{
p.parent.right = x;
}
x.left = p;
// 更新 p 的父亲
p.parent = x;
}
8.2、右旋
private
只做旋转,不变色
/**
* 右旋
* -------------------------------------
* P X
* // \ // \\
* X c 右旋后> a P
* // \ / \
* a b b c
* -------------------------------------
*
* @param p
*/
private void rotateRight(Node p) {
// 参数有效性检测
if (p == null || p.right == null) {
return;
}
// 当前节点为 p,它的左子节点为 x
Node x = p.left;
// 右旋后:
// 1、p、x节点的父亲、儿子都发生了变化
// 2、x右子节点的父亲发生变化,儿子不变
// 3、p的父亲的儿子发生变化
// 更新 x 的右子
if(x.right != null){
x.right.parent = p;
}
// 更新 p 的左子
p.left = x.right;
// 更新 x
x.parent = p.parent;
// 更新 p 的父亲
if(p.parent == null){
root = x;
}
else if(p.parent.right == p){
p.parent.right = x;
}
else{
p.parent.left = x;
}
x.right = p;
// 更新 p 的父亲
p.parent = x;
}
8.3、添加后调整分析
1)向2-3-4树中的1节点添加
1节点就是根节点,相当于空树
直接添加,不需要调整
2)向2-3-4树中的2节点添加
2节点就是包含:1个元素,有2个分叉
2节点都是黑色
直接添加,上黑下红;不需要调整
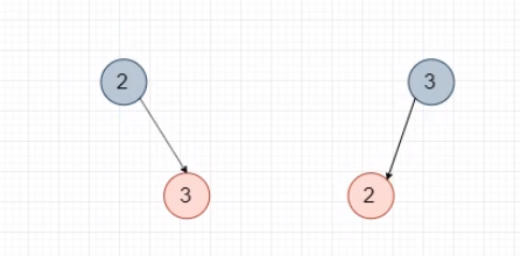
3)向2-3-4树中的3节点添加
3节点就是包含:2个元素,有3个分叉
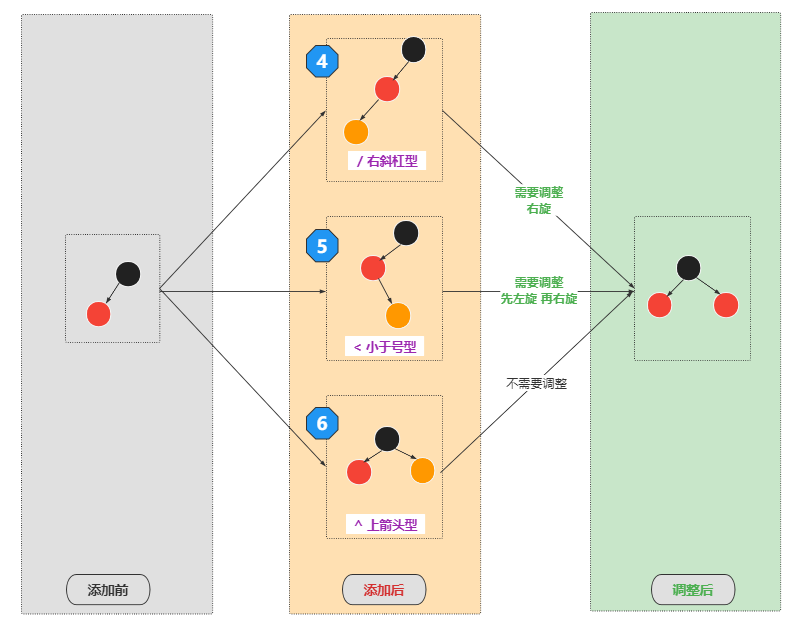
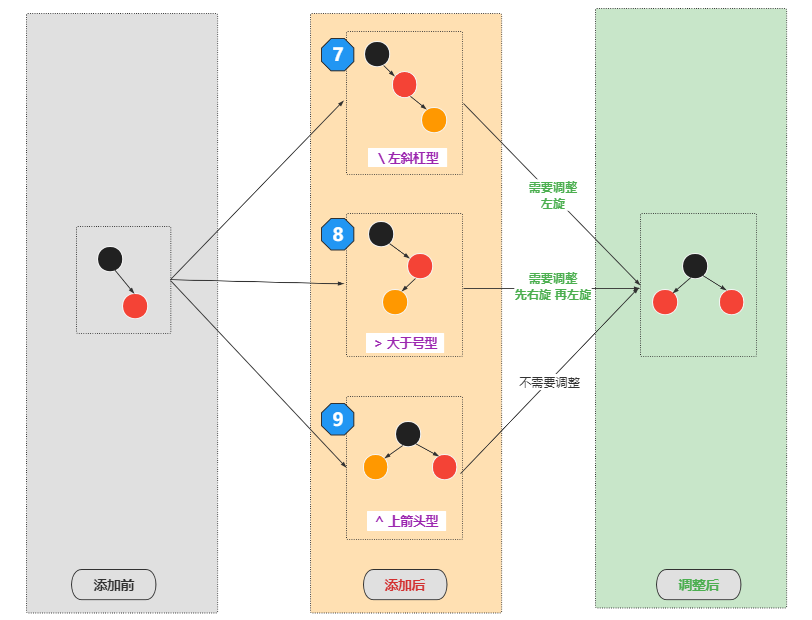
4)向2-3-4树中的4节点添加
4节点就是包含:3个元素,有4个分叉
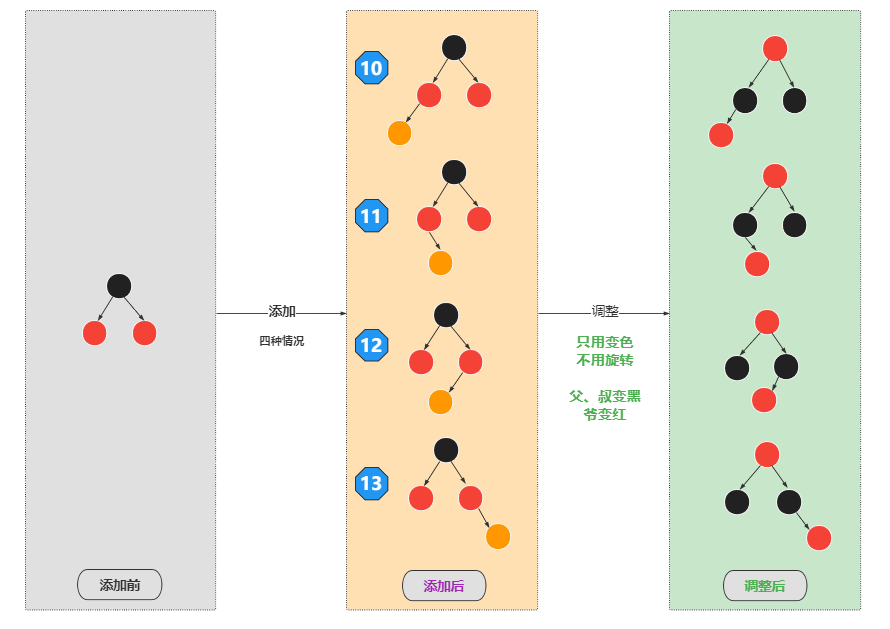
如果爷爷节点为根节点,则变黑
5)分析
-
节点需要调整的条件
-
不为null
-
不为根
-
父节点为红色
-
-
具体分类:
- 4、5、7、8 需要旋转
- 10、11、12、13 需要变色
-
循环操作
6)fixAfterPut()
private
/**
* 添加后调整
* 旋转、变色
*
* @param x
*/
private void fixAfterPut(Node x) {
// 新结点为红色
x.color = RED;
// x不为null,且不为root,父节点为红色时才需要调整
// 4、5、7、8 需要旋转、变色
// 10、11、12、13 需要变色
while (x != null && x != root && x.parent.color == RED) {
// 爷爷的左侧
// 【4、5、10、11 四种情况】
// x的父节点是爷爷的左孩子
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// 叔叔节点
Node y = rightOf(parentOf(parentOf(x)));
// 叔叔是红色:【10、11两种情况】只需要变色
if(colorOf(y) == RED){
// 父亲变黑
setColor(parentOf(x),BLACK);
// 叔叔变黑
setColor(y,BLACK);
// 爷爷变红
setColor(parentOf(parentOf(x)),RED);
// 以爷爷为起点,循环操作
x = parentOf(parentOf(x));
}
// 【4、5两种情况】旋转、变色
else{
// 【情况5】先左旋,变成4
if (x == rightOf(parentOf(x))) {
// x 指向父亲
x = parentOf(x);
// 以父亲为支点左旋
rotateLeft(x);
}
// 【情况4】变色、右旋
// 父亲变黑
setColor(parentOf(x), BLACK);
// 爷爷变红
setColor(parentOf(parentOf(x)), RED);
// 以爷爷为支点右旋
rotateRight(parentOf(parentOf(x)));
}
}
// 爷爷的右侧
// 【7、8、12、13 四种情况】
// x的父节点是爷爷的右孩子
else{
// 叔叔节点
Node y = leftOf(parentOf(parentOf(x)));
// 叔叔是红色:【12、13两种情况】只需要变色
if(colorOf(y) == RED){
// 父亲变黑
setColor(parentOf(x),BLACK);
// 叔叔变黑
setColor(y,BLACK);
// 爷爷变红
setColor(parentOf(parentOf(x)),RED);
// 以爷爷为起点,循环操作
x = parentOf(parentOf(x));
}
// 【7、8两种情况】旋转、变色
else{
// 【情况8】先右旋,变成7
if (x == leftOf(parentOf(x))) {
// x 指向父亲
x = parentOf(x);
// 以父亲为支点右旋
rotateRight(x);
}
// 【情况7】变色、左旋
// 父亲变黑
setColor(parentOf(x), BLACK);
// 爷爷变红
setColor(parentOf(parentOf(x)), RED);
// 以爷爷为支点左旋
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 根节点黑色
root.color = BLACK;
}
8.4、辅助方法
1、父节点 parentOf()
/**
* 获取父节点
*
* @param node
* @return
*/
private Node parentOf(Node node) {
return node != null ? node.parent : null;
}
2、左子节点 leftOf()
/**
* 获取左子节点
*
* @param node
* @return
*/
private Node leftOf(Node node) {
return node != null ? node.left : null;
}
3、右子节点 rightOf()
/**
* 获取右子节点
*
* @param node
* @return
*/
private Node rightOf(Node node) {
return node != null ? node.right : null;
}
4、设置颜色 setColor()
/**
* 设置颜色
* @param node
* @param color
*/
private void setColor(Node node, boolean color) {
if (node != null) {
node.color = color;
}
}
9、删除
9.1、思路
先删除,后调整
红黑树是平衡树,删除的节点只可能是叶子节点,或者是叶子节点的父节点(单叶子,没有兄弟)
即:叶子层,或叶子的上一层,不会再向上
如果要删除上面层的节点,会先用替代节点替换下来,转换成叶子或叶子的上一层节点
- 如果是叶子节点,直接删除
- 如果只有一个子节点,用子叶点替代
- 如果有两个子节点,需要用替代节点(前驱或后继),转换成上面两种情况
9.2、remove()
public
/**
* 删除 key 节点
* @param key
* @return
*/
public V remove(K key){
// 得到目标节点
Node p = getNode(key);
if(p==null){
return null;
}
V oldValue = p.value;
// 删除
deleteNode(p);
return oldValue;
}
9.3、deleteNode()
private
/**
* 删除目标节点 p
* 只修改指针
* 旋转、变色用其它方法
*
* @param p
*/
private void deleteNode(Node p) {
// 数量减1
n--;
// 如果p有两个孩子:用后继节点替换
// 有两个孩子对应于2-3-4树中的4节点(4个分叉,每个孩子各2个)
if (p.left != null && p.right != null) {
// 后继节点
Node s = successor(p);
// 【值传递】用后继节点替换p的key和value;p的left、right、parent指向并不变
p.key = s.key;
p.value = s.value;
// 【引用传递】更新p的指向:指向后继结点;相当于交换位置
p = s;
}
/**
* 此时有两个孩子的情况已被过滤掉;p是被删除节点,有三种情况:
* 1、有一个孩子:对应于2-3-4树中的3节点(3个分叉)
* 2、没有孩子:对应于2-3-4树中的2节点(2个分叉)
* 3、没有孩子的根节点:对应于2-3-4树中的1节点(1个分叉)
*/
// ----------针对上面三种情况,开始删除、调整----------
// 替补节点:就是要填补【被删除节点p】位置的节点
Node replacement = (p.left != null ? p.left : p.right);
// 有一个孩子:对应于2-3-4树中的3节点(3个分叉)
// 黑父亲 + 红独子
if (replacement != null) {
// 更新替补节点的父亲:跳过当前父亲,指向父亲的的父亲,因为当前父亲要被删掉
replacement.parent = p.parent;
// -----更新p父亲的孩子指针-----
// p的父亲是null,p是根节点:替补节点成为根
if (p.parent == null) {
root = replacement;
}
// p是父亲的左孩子
else if (p == p.parent.left) {
p.parent.left = replacement;
}
// p是父亲的右孩子
else {
p.parent.right = replacement;
}
// p的父亲和孩子指针更新完毕,开始删除p
// 把p的三个指针都设为null,从树中脱落,等待GC回收
p.parent = p.left = p.right = null;
// 如果p是黑色节点,开始调整
if (p.color == BLACK) {
// 【调整情况一:黑父亲 + 红独子(3节点)】
// 调整的是替补节点:红孩子
fixAfterDeletion(replacement);
}
}
// 没有孩子的根节点:对应于2-3-4树中的1节点(1个分叉)
else if (p.parent == null) {
root = null;
}
// 没有孩子:对应于2-3-4树中的2节点(2个分叉)
else {
// 被删除节点是黑色,开始调整
if (p.color == BLACK) {
// 【调整情况二:无孩子黑节点(2节点)】
// 调整的是被删除节点,没有替补节点
fixAfterDeletion(p);
}
// 更新【p】和【p的父亲】的指针
if (p.parent != null) {
// 更新【p的父亲】的孩子指针
// p是它父亲的左孩子
if (p == p.parent.left) {
p.parent.left = null;
}
// p是它父亲的右孩子
else if (p == p.parent.right) {
p.parent.right = null;
}
// 更新【p】的指针:p没有孩子,只更新父亲指针
p.parent = null;
}
}
}
10、删除后调整
10.1、删除调整分析
1)删除目标:2-3-4树叶子
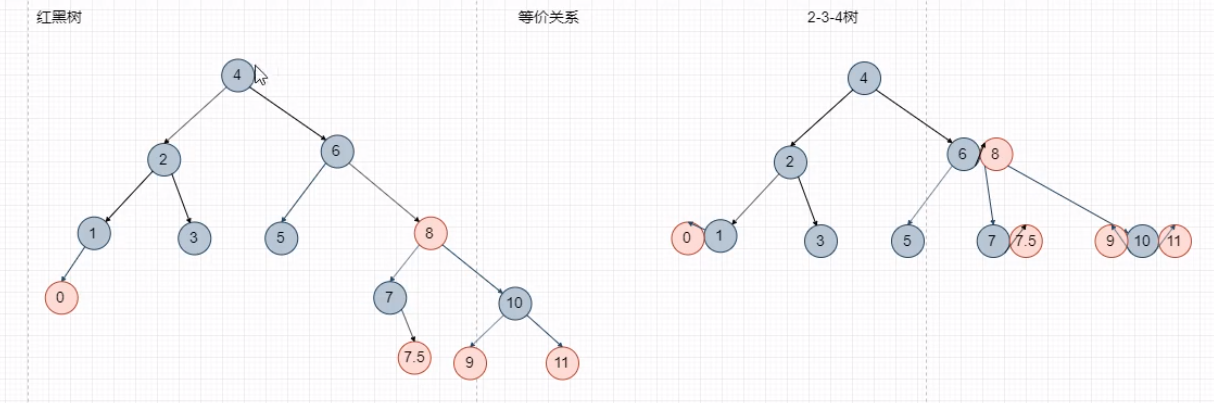
-
红黑树上要删除的节点,一定是 叶子节叶,或 叶子的上一层节点
叶子的上一层节点:这类节点只有一侧叶子,如果有左右叶子,需要先替换
-
如果是其它情况会通过替换节点,转换成上面的情况,再删除
-
通过等价关系,可以看出被删除节点,就是2-3-4树中的叶子节点
2-3-4树的叶子节点共有三种情况:(1节点表示空树)
- 2节点
- 3节点
- 4节点
2)【删3、4节点】 直接删
2-3-4树中的3节点、4节点可以直接删,删除后不会破坏对应红黑树的平衡
| 2-3-4树 | 红黑树 | 操作 |
|---|---|---|
| 3节点:2个元素、3个分叉 | 黑父亲 + 1个红儿子 | 删儿子:直接删 删父亲:用儿子替,再变黑 |
| 4节点:3个元素、4个分叉 | 黑父亲 + 2个红儿子 | 删儿子:直接删 删父亲:用儿子替,再变黑 |
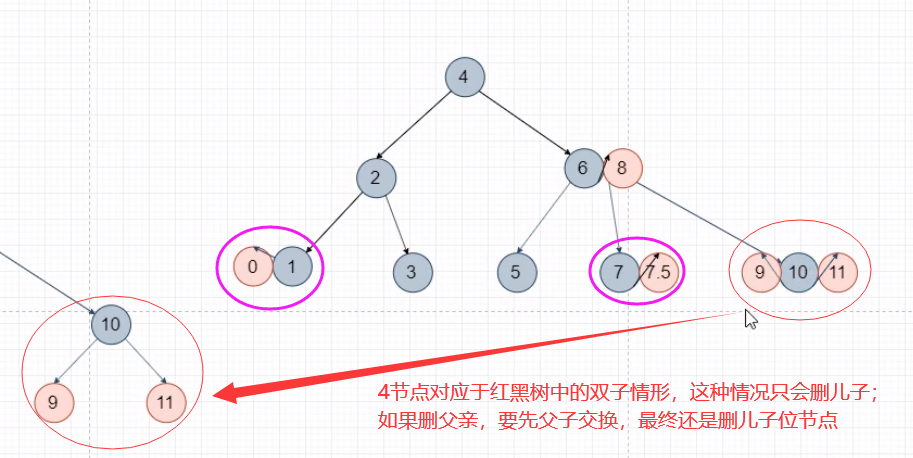
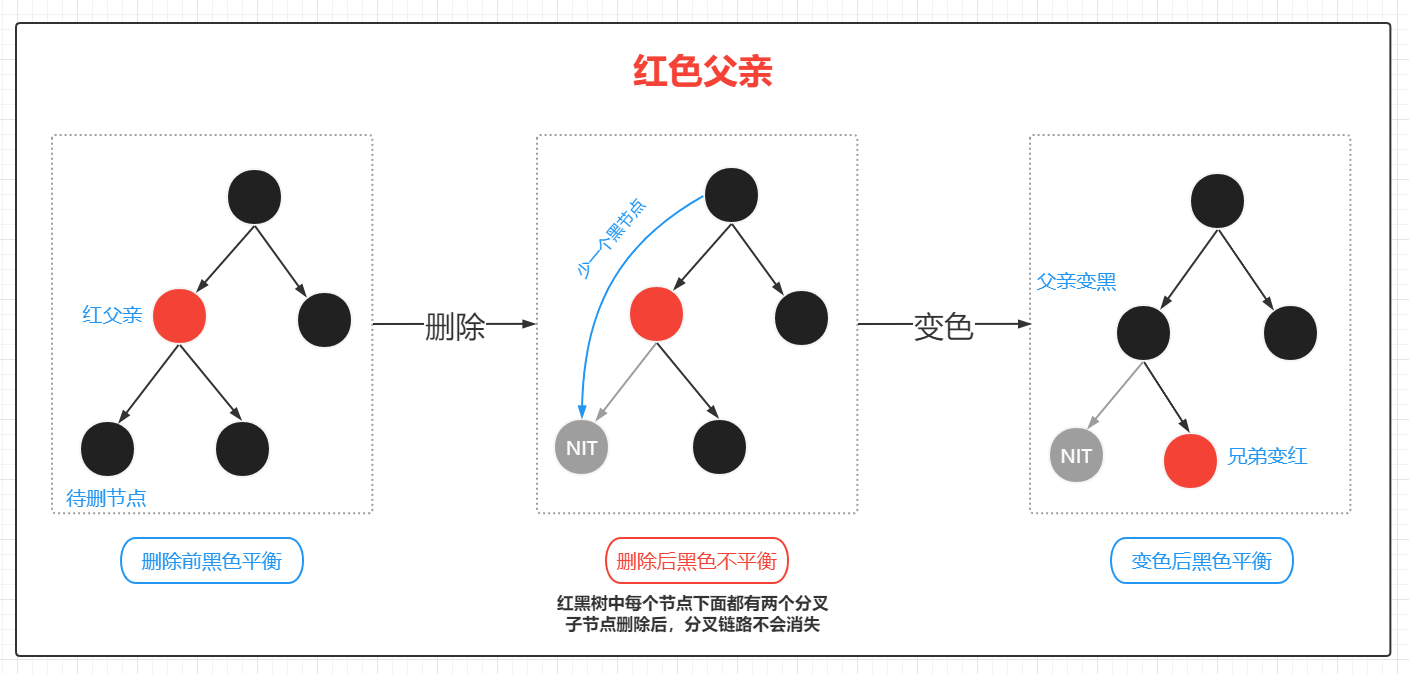
3)【删2节点】兄弟3、4节点
由于2节点没有孩子,2节点转换为红黑树后是黑色,删除黑色会打破平衡,需要先找替换节点,向下没有儿子,只能向上找父亲
自已搞不定,需要跟兄弟借,兄弟不借,找父亲借,父亲下来,兄弟找人上去替父亲当家
兄弟有得借
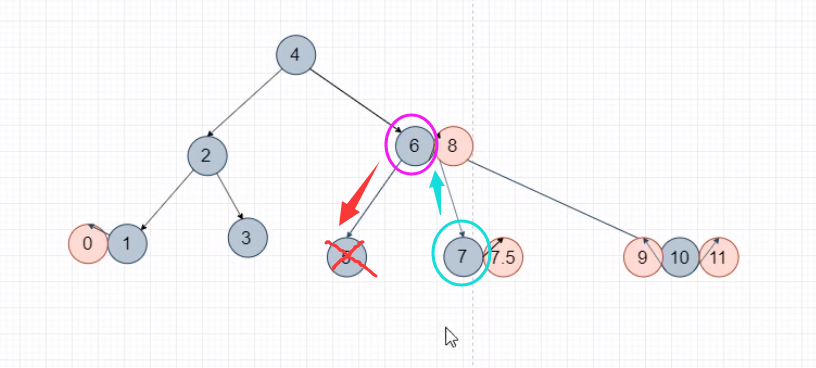
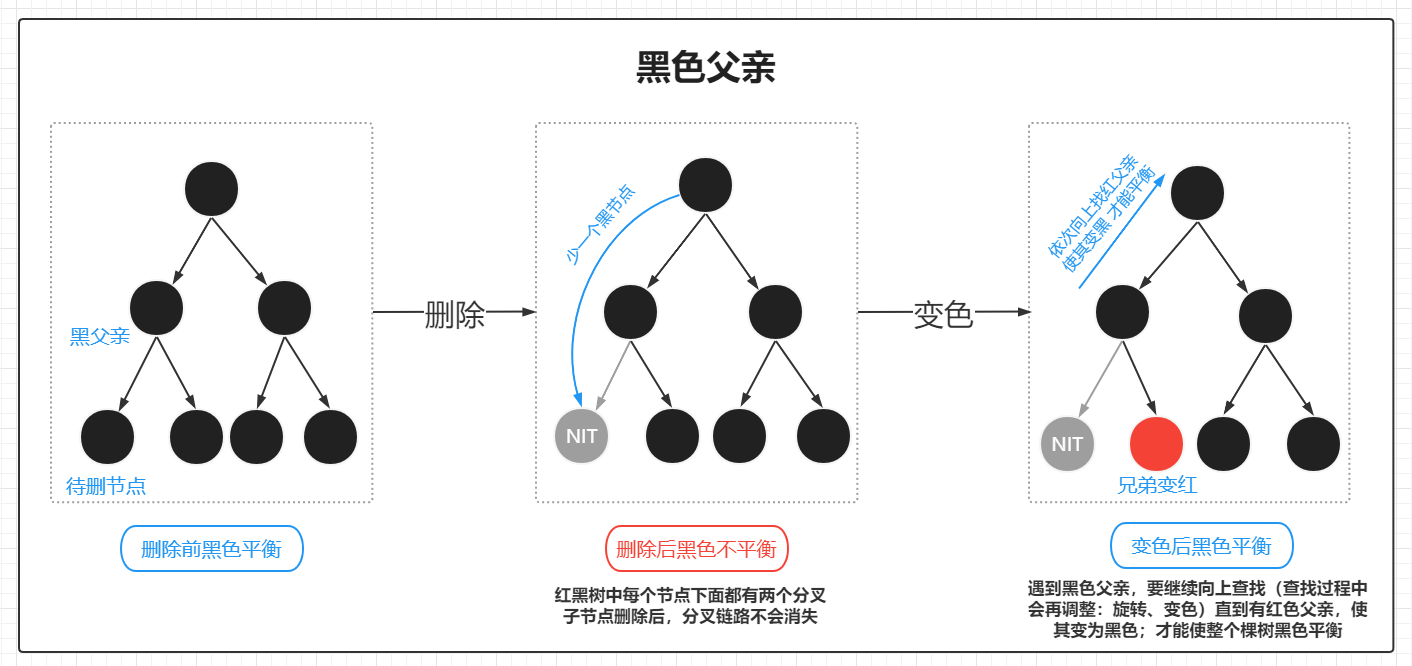
4)【删2节点】兄弟2节点
自已搞不定,兄弟也没有
10.2、fixAfterDeletion()
private
/**
* 删除后调整
* 旋转、变色
*
* @param x
*/
private void fixAfterDeletion(Node x) {
/**
* 不是根节点,并且是黑色节点,才需要调整
* 【调整情况二:无孩子黑节点(2节点)】
* 由于2节点没有孩子,2节点转换为红黑树后是黑色
* 删除黑色会打破平衡,需要先找替换节点,向下没有儿子,只能向上找父亲
*/
while (x != root && colorOf(x) == BLACK) {
// x 是父亲左孩子
if (x == leftOf(parentOf(x))) {
// 找兄弟借
// 兄弟节点:因为自已是左孩子,兄弟在右边
Node sib = rightOf(parentOf(x));
// 如果sib是红色,从2-3-4树中看,不是真正的兄弟节点,找真正的兄弟节点(黑色)
if (colorOf(sib) == RED) {
// 自已变黑
setColor(sib, BLACK);
// 父亲变红
setColor(parentOf(x), RED);
// 以父亲为支点左旋
rotateLeft(parentOf(x));
// 此时父亲的右孩子是真正的兄弟
sib = rightOf(parentOf(x));
}
// -----两种小情况-----
// 1、兄弟没得借:单身
// colorOf(leftOf(sib)) == BLACK 等价于 leftOf(sib) == null
if (colorOf(leftOf(sib)) == BLACK && colorOf(rightOf(sib)) == BLACK) {
/**
* 自已和兄弟都是黑色单身
* 自已被删后,为了保持黑平衡,兄弟由黑变红
* 然后,x 指向父亲,依次向上查找,直到找到一个红色父亲,退出循环
* 最后,把红色父亲变黑,实现整棵树黑平衡(变黑操作在退出循环后,由本方法最后一句实现)
*/
setColor(sib,RED);
x = parentOf(x);
}
// 2、兄弟有得借:3节点、4节点
else {
// -----再分两种小情况------
/**
* 【1、兄弟是3节点:有左孩子】
* --------------------------
* 有左孩子,没有右孩子
* 先变色,后右旋,把左孩子情况转换成右孩子情况
* 转换后【3节点】操作和【4节点】一致
* --------------------------
* colorOf(rightOf(sib)) == BLACK 等价于 rightOf(sib) == null
*/
if (colorOf(rightOf(sib)) == BLACK) {
// 兄弟的左孩子变黑
setColor(leftOf(sib), BLACK);
// 兄弟变红
setColor(sib, RED);
// 兄弟右旋
rotateRight(sib);
// 右旋后,当前节点x的父亲的右孩子成为兄弟,就是原来兄弟的左孩子
sib = rightOf(parentOf(x));
}
/**
* 【2、兄弟是4节点;或者兄弟是3节点,有右孩子】
* -------------------------
* 以当前节点 x 的父亲为支点左旋
* 左旋前先变色
* -------------------------
*/
// 兄弟颜色变为父亲颜色
// 兄弟是要上位,替换父亲位置的
setColor(sib, colorOf(parentOf(x)));
// 父亲颜色变黑
// 因为要删除的目标是没有孩子的【黑节点x】,父亲要下来替换x,为了保持黑平衡,父亲要变黑
setColor(parentOf(x), BLACK);
// 兄弟右孩子变黑
// 因为兄弟的右孩子,是要上位,替换兄弟位置的
// 真正的兄弟都是黑色,为了保持黑平衡,兄弟的右孩子要变黑
setColor(rightOf(sib), BLACK);
// 以当前节点 x 的父亲为支点左旋
rotateLeft(parentOf(x));
// 本轮调整完毕,结束循环
x = root;
}
}
// x 是父亲右孩子
else {
// 找兄弟借
// 兄弟节点:因为自已是右孩子,兄弟在左边
Node sib = leftOf(parentOf(x));
// 如果sib是红色,从2-3-4树中看,不是真正的兄弟节点,找真正的兄弟节点(黑色)
if (colorOf(sib) == RED) {
// 自已变黑
setColor(sib, BLACK);
// 父亲变红
setColor(parentOf(x), RED);
// 以父亲为支点右旋
rotateRight(parentOf(x));
// 此时父亲的左孩子是真正的兄弟
sib = leftOf(parentOf(x));
}
// -----两种小情况-----
// 1、兄弟没得借:单身
// colorOf(leftOf(sib)) == BLACK 等价于 leftOf(sib) == null
if (colorOf(leftOf(sib)) == BLACK && colorOf(rightOf(sib)) == BLACK) {
/**
* 自已和兄弟都是黑色单身
* 自已被删后,为了保持黑平衡,兄弟由黑变红
* 然后,x 指向父亲,依次向上查找,直到找到一个红色父亲,退出循环
* 最后,把红色父亲变黑,实现整棵树黑平衡(变黑操作在退出循环后,由本方法最后一句实现)
*/
setColor(sib,RED);
x = parentOf(x);
}
// 2、兄弟有得借:3节点、4节点
else {
// -----再分两种小情况------
/**
* 【1、兄弟是3节点:有右孩子】
* --------------------------
* 有右孩子,没有左孩子
* 先变色,后左旋,把右孩子情况转换成左孩子情况
* 转换后【3节点】操作和【4节点】一致
* --------------------------
* colorOf(leftOf(sib)) == BLACK 等价于 leftOf(sib) == null
*/
if (colorOf(leftOf(sib)) == BLACK) {
// 兄弟的右孩子变黑
setColor(rightOf(sib), BLACK);
// 兄弟变红
setColor(sib, RED);
// 兄弟左旋
rotateLeft(sib);
// 左旋后,当前节点x的父亲的左孩子成为兄弟,就是原来兄弟的右孩子
sib = leftOf(parentOf(x));
}
/**
* 【2、兄弟是4节点;或者兄弟是3节点,有左孩子】
* -------------------------
* 以当前节点 x 的父亲为支点右旋
* 右旋前先变色
* -------------------------
*/
// 兄弟颜色变为父亲颜色
// 兄弟是要上位,替换父亲位置的
setColor(sib, colorOf(parentOf(x)));
// 父亲颜色变黑
// 因为要删除的目标是没有孩子的【黑节点x】,父亲要下来替换x,为了保持黑平衡,父亲要变黑
setColor(parentOf(x), BLACK);
// 兄弟左孩子变黑
// 因为兄弟的左孩子,是要上位,替换兄弟位置的
// 真正的兄弟都是黑色,为了保持黑平衡,兄弟的左孩子要变黑
setColor(leftOf(sib), BLACK);
// 以当前节点 x 的父亲为支点右旋
rotateRight(parentOf(x));
// 本轮调整完毕,结束循环
x = root;
}
}
}
/**
* 以下代码适用于两种情况
* ============== 1 ================
* -----如果 x 是红色,上面代码不执行-----
* 【调整情况一:黑父亲 + 红独子(3节点)】
* 这种情况 x 是红孩子,真正删除的是它的黑父亲
* x 作为替补,替换父亲的位置
* 需要调整的是 x
* 为了保持黑平衡,只需要把 x 染黑即可
* 父亲已亡,红孩子升级为黑父亲
* ============== 2 ================
* 两个黑兄弟,删除一个后,另一个变红
* 为了保持黑平衡,会循环查找红父亲
* 找到后把红父亲变黑
*/
setColor(x, BLACK);
}
参考:
视频:https://www.bilibili.com/video/BV1864y1S7si
源码:java.util.TreeMap (简直是艺术品)

源码作者:Josh Bloch and Doug Lea(道格·利)
本文来自博客园,作者:土味儿,转载请注明原文链接:https://www.cnblogs.com/tuwer/articles/15269133.html

 浙公网安备 33010602011771号
浙公网安备 33010602011771号