基于RSA的消息盲签名（控制台Edition）
盲签名体制是保证参与者匿名性的基本密码协议。自从出现对电子现金技术的研究以来，盲签名已成为其最重要的实现工具之一。
一个盲签名体制是一个协议，包括两个实体:消息发送者和签名者。它允许发送者让签名者对给定的消息签名，并且没有泄露关于消息和消息签名的任何信息。
1982年，Chaum首次提出盲签名的概念，并利用盲签名技术提出了第一个电子现金方案。利用盲签名技术可以完全保护用户的隐私权，因此，盲签名技术在诸多电子现金方案中广泛使用。
盲数字签名的基本原理是两个可换的加密算法的应用，第一个加密算法是为了隐蔽信息，可称为盲变换，第二个加密算法才是真正的签名算法。
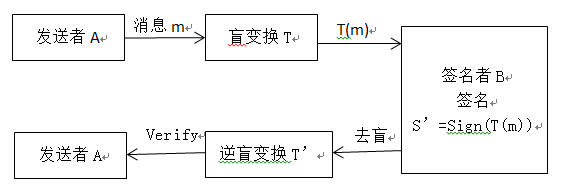
盲签名的特点是：
- 消息的内容对签名者是盲的；
- 签名者不能将所签文件T(m)和实际要签的文件m联系起来，即使他保存所有签过的文件，也不能确定出所签文件的真实内容。
基于RSA的盲签名体制
签名者B选两个大素数p、q，计算n=pq，随机选择e（不必是素数）满足
，再由
求出d，最后选择一个单向函数f（即老外常说的TrapDoor函数）。公开n、e和f。（如果选择一个单向函数作为f（反向计算几乎不可能），就可以公开f;但如果处于某种原因使用较简单的函数作为f，就不可以公开了，否则Bob就有可能知道内容了）
设发送者Alice要求签名者Bob对消息m进行盲签名。则Alcie和Bob遵从如下协议：
（1)Alice随机选择盲因子k结合盲化函数f计算：
并将m'发送给Bob;
(2) Bob接收到m’后，用RSA的私钥d对其进行签名：
并将S’发送会Alice;
(3)Alice收到s’后，计算来自Bob的签名S:
Alice通过验证 
来判断S是否是Bob的签名。
分析：在签名过程中，Bob从未看到过m和对m的盲签名s（实际上是对f(m)的盲签名），所以他无法将(m,s)和(m’,s’)联系起来，因而Bob无法确定他所签文件的内容。
程序实现时非常要注意的一点：
在对S’去盲计算真实签名S时，要使用S=S’/k，而不能使用
。因为请求签名方没有私钥d（要是有的话，还请求Bob干嘛呀-.-）。
但是，直接使用S’=S/k，在程序计算上是不可行的。为什么这么说呢？
举个例子: ，直接从左向右计算的话，结果为4。但是如果根据(a*b) mod c=a mod c * b mod c的话，就变成
，结果为1（计算机整数相除默认结果取整）。这就出现了窘境。岂不是两个式子都不能用，难道盲签名无法真正投入实际应用？NO.
解决方法：既然原因是因为本来可以消掉分数的部分给“模掉”了，那么我们就给它加回来：给13加上若干个15，使得其可以整除7，然后整除7模15，done.
但是，这个运算在理论上是可行的，你看下面的证明没有任何问题：
首先给个结论，根据费马小定理，下面的等式是成立的：
证明：
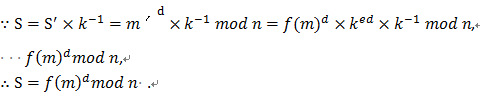
代码贴上：
#include <iostream>
using std::cout;
using std::endl;
#include <cstdlib>
#include <iomanip>
using std::hex;
#include <string>
using std::string;
#include <rsa.h>
using CryptoPP::RSA;
#include <integer.h>
using CryptoPP::Integer;
#include <osrng.h>
using CryptoPP::AutoSeededRandomPool;
int main(int argc, char** argv)
{
cout<<"======================================================="<<endl;
cout<<" 基于RSA的盲签名演示程序 "<<endl;
cout<<"======================================================="<<endl;
AutoSeededRandomPool prng;
/////////////////////////////////////////////////////////
/*
RSA::PrivateKey privKey;
privKey.GenerateRandomWithKeySize(prng, 128);
RSA::PublicKey pubKey(privKey);
cout << "modulus: " << hex << privKey.GetModulus() << endl;
cout << "private exp: " << hex << privKey.GetPrivateExponent() << endl;
cout << "public exp: " << hex << privKey.GetPublicExponent() << endl;
cout << endl;
*/
/////////////////////////////////////////////////////////
Integer n("0xbeaadb3d839f3b5f"), e("0x11"), d("0x21a5ae37b9959db9");
RSA::PrivateKey privKey;
privKey.Initialize(n, e, d);
RSA::PublicKey pubKey;
pubKey.Initialize(n, e);
//输出相关参数信息
cout<<"选取的2个素数:"<<"p:"<<hex<<privKey.GetPrime1()<<"\tq:"<<hex<<privKey.GetPrime2()<<endl;
cout<<"公钥(e,n):"<<"("<<hex<<e<<","<<hex<<n<<")"<<endl;
cout<<"私钥(d,n):"<<"("<<hex<<d<<","<<hex<<n<<")\n\n"<<endl;
/////////////////////////////////////////////////////////
string message, recovered;
Integer m, fm,c, r, k(128), m_, s_, s;
message = "NCEPU Sci&Teque";
cout << "message原文: " << message << endl;
// Treat the message as a big endian array
m = Integer((const byte *)message.data(), message.size());
cout << "盲化的消息m: " << hex << m << endl;
// Encrypt and Blind
//c = pubKey.ApplyFunction(m);
//cout << "c: " << hex << c << endl;
fm=m;
m_=a_exp_b_mod_c(k,e,n);
m_=m_*fm%n;
cout<<"加密后的盲化消息m_:"<<hex<<m_<<endl<<endl<<endl;
// Decrypt
//r = privKey.CalculateInverse(prng, c);
//cout << "r: " << hex << r << endl;
//Sign
s_=a_exp_b_mod_c(m_,d,n);
cout<<"签名后的加密消息s_:"<<hex<<s_<<endl;
//unblind
for(int nani=1;;nani++)
{
s_+=n;
if(s_%k==0)
{
s=s_/k%n;
cout<<"nani:"<<nani<<endl;//29
cout<<"s:"<<hex<<s<<endl;
break;
}
}
//验证是否与上面的相等
s=a_exp_b_mod_c(fm,d,n);
cout<<"s:"<<hex<<s<<endl;
cout<<"解盲后的签名s:"<<endl;
cout<<"\n开始验证签名的合法性.."<<endl;
bool bVerify=true;
if(fm%n == a_exp_b_mod_c(s,e,n))
{
bVerify=true;
cout<<"Verify Success!\n"<<endl;
}
else
{
bVerify=false;
cout<<"Vefify Failed.\n"<<endl;
}
// Round trip the message
if(bVerify)
{
cout<<"\n开始解密消息.."<<endl;
size_t req=fm.MinEncodedSize();
recovered.resize(req);
fm.Encode((byte*)recovered.data(),recovered.size());
cout<<"解密后的消息recovered:"<<recovered<<endl;
cout<<"解密成功！"<<endl;
}
system("pause");
return 0;
}
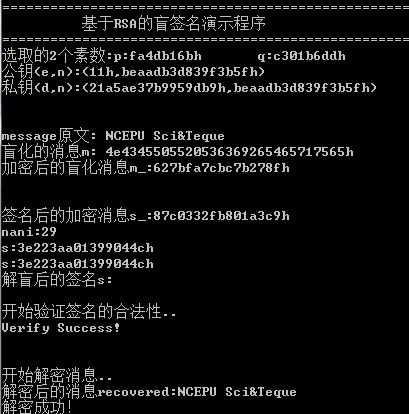
结果附上：
浙公网安备 33010602011771号