数据结构与算法

1. 数据结构定义

数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。

• 数组：物理存储单元上连续、顺序的存储结构
• 链表：链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。
• 队列：队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。队列的实现方式如下：
  • 基于链表来实现队列。
  • 使用linkedList来实现队列。
  • 使用两个栈来实现一个队列。
• 栈：栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。
• 堆：堆通常是一个可以被看做一棵完全二叉树的数组对象。将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆。建堆时间复杂度O（n），堆总是满足下列性质：堆总是一棵完全二叉树；堆中某个结点的值总是不大于或不小于其父结点的值；
• 散列表：（Hash table，也叫哈希表），是根据关键码值(Key value)而直接进行访问的数据结构
• 树：是元素的集合。树有多个节点(node)，用以储存元素。某些节点之间存在一定的关系，用连线表示，连线称为边(edge)。边的上端节点称为父节点，下端称为子节点。树像是一个不断分叉的树根。严格定义：
  • 树是元素的集合。
  • 该集合可以为空。这时树中没有元素，我们称树为空树 (empty tree)。
  • 如果该集合不为空，那么该集合有一个根节点，以及0个或者多个子树。根节点与它的子树的根节点用一个边(edge)相连。
• 二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。
• 图：是由顶点的有穷非空集合和顶点之间边的集合组成，通过表示为G(V,E)，其中，G标示一个图，V是图G中顶点的集合，E是图G中边的集合。

 

1. 堆的创建、插入、删除、堆排序

• 堆的插入：在已经建成的最小堆的后面插入元素，堆的结构可能被破坏，再向上调整使其满足性质。
• 堆的删除：删除时每次删除堆顶元素

  删除方法：

1. 将堆中最后一个元素代替堆顶元素。
2. 将堆中元素个数减少一个，相当于将堆中最后一个元素删除。
3. 此时堆的结构可能被破坏，在向下调整使其满足性质。

• 堆排序：
  • 将堆顶元素与第size-1个元素交换。
  • hp->size–
  • 将其余的元素调整为最小堆
  • 重复1、2、3步hp->size-1次。

 

1. 树

• AVL树

平衡二叉搜索树（Self-balancing binary search tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。查询logN、增删的复杂度N。

• 哈夫曼树

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

 

1. 跳表

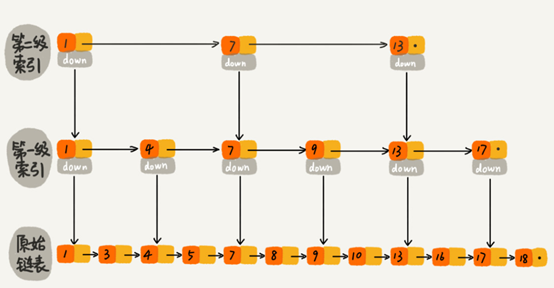
跳表，是基于链表实现的一种类似"二分"的算法。它可以快速地实现增，删，改，查操作。这种链表加多级索引的结构，就叫做跳表。跳表的查询时间复杂度可以达到O(logn)。跳表也可以实现高效的动态更新，定位到要插入或者删除数据的位置需要的时间复杂度为O(logn)，最坏O(N)。

在插入的时候，我们需要考虑将要插入的数据也插入到索引中去。在这里使用的策略是通过随机函数生成一个随机数K，然后将要插入的数据同时插入到k级以下的每级索引中。https：//www.jianshu.com/p/43039adeb122

 

1. 排序算法

见网址（https：//www.cnblogs.com/onepixel/articles/7674659.html）

• 排序算法稳定性
  • 定义：指待排序的序列中有两相邻元素相等，排序之后它们的先后顺序不变。
• 不同条件下，排序方法的选择

1. 若n较小(如n≤50)，可采用直接插入或直接选择排序。当记录规模较小时，直接插入排序较好；否则因为直接选择移动的记录数少于直接插入，应选直接选择排序为宜。
2. 若文件初始状态基本有序(指正序)，则应选用直接插入、冒泡或随机的快速排序为宜；
3. 若n较大，则应采用时间复杂度为O(nlgn)的排序方法：快速排序、堆排序或归并排序。
   1. 快速排序是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；
   2. 堆排序所需的辅助空间少于快速排序，并且不会出现快速排序可能出现的最坏情况。这两种排序都是不稳定的。
   3. 若要求排序稳定，则可选用归并排序。
4. TopK或优先队列通常用堆排序来实现

• 快速排序基准值的选取及优化：三数取中+插排+聚集相等元素（在一次分割结束后，可以把与Key相等的元素聚在一起，继续下次分割时，不用再对与key相等元素分割）

  https://blog.csdn.net/lxk2017/article/details/102779042

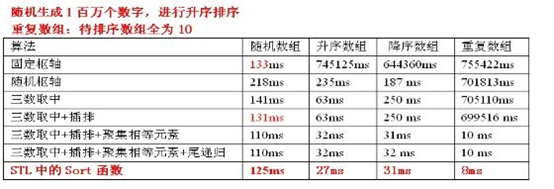
void QSort(int arr[],int low,int high)

{

    int first = low;

    int last = high;

 

    int left = low;

    int right = high;

 

    int leftLen = 0;

    int rightLen = 0;

 

    //待排序序列的长度小于10使用插入排序

    if (high - low + 1 < 10)

    {

        InsertSort(arr,low,high);

        return;

    }

    

    //一次分割

    int key = SelectPivotMedianOfThree(arr,low,high);//使用三数取中法选择枢轴

        

    while(low < high)

    {

        while(high > low && arr[high] >= key)

        {

//处理相等元素

            if (arr[high] == key)

            {

                swap(arr[right],arr[high]);

                right--;

                rightLen++;

            }

            high--;

        }

        arr[low] = arr[high];

        while(high > low && arr[low] <= key)

        {

            if (arr[low] == key)

            {

                swap(arr[left],arr[low]);

                left++;

                leftLen++;

            }

            low++;

        }

        arr[high] = arr[low];

    }

    arr[low] = key;

 

    //一次快排结束

    //把与枢轴key相同的元素移到枢轴最终位置周围

    int i = low - 1;

    int j = first;

    while(j < left && arr[i] != key)

    {

        swap(arr[i],arr[j]);

        i--;

        j++;

    }

    i = low + 1;

    j = last;

    while(j > right && arr[i] != key)

    {

        swap(arr[i],arr[j]);

        i++;

        j--;

    }

    QSort(arr,first,low - 1 - leftLen);

    QSort(arr,low + 1 + rightLen,last);

}

 

/*函数作用：取待排序序列中low、mid、high三个位置上数据，选取他们中间的那个数据作为枢轴*/

int SelectPivotMedianOfThree(int arr[],int low,int high)

{

//计算数组中间的元素的下标

    int mid = low + ((high - low) >> 1);

    //使用三数取中法选择枢轴

//目标: arr[mid] <= arr[high]

    if (arr[mid] > arr[high])

    {

        swap(arr[mid],arr[high]);

    }

//目标: arr[low] <= arr[high]

    if (arr[low] > arr[high])

    {

        swap(arr[low],arr[high]);

    }

//目标: arr[mid] >= arr[low]

    if (arr[low] > arr[mid])

    {

        swap(arr[low],arr[mid]);

    }

    //此时，arr[low] <= arr[mid] <= arr[high]

    return arr[mid];

}

 

1. Bitmap位图算法

https：//blog.csdn.net/lucky52529/article/details/90172264

位图是指内存中连续的二进制位，用于对大量的整型数据做去重和查询。Bit-map就是用一个bit位来标记某个元素对应的Value，而Key即是该元素。由于采用了Bit为单位来存储数据，因此在存储空间方面，可以大大节省。

• bitmap应用

1）可进行数据的快速查找、判重、删除，一般来说数据范围是int的10倍以下。

2）去重数据而达到压缩数据

位图只是可以映射数字类型的数据，变成字符串以及其他文件好像就不再那么得心应手了，这时就要使用布隆过滤器

 

1. 布隆过滤器

bloom算法类似一个位图，用来判断某个元素（key）是否在某个集合中。和一般的位图不同的是，这个算法无需存储key的值，对于每个key，只需要k个比特位，每个存储一个标志，用来判断key是否在集合中。

应用场景：比如网络爬虫抓取时url去重，邮件提供商反垃圾黑名单Email地址去重，之所以需要k个比特位是因为我们大多数情况下处理的是字符串，那么不同的字符串就有可能映射到同一个位置，产生冲突。

优点：不需要存储key，节省空间

缺点：算法判断key在集合中时，有一定的概率key其实不在集合中，已经映射的数据无法删除

 

1. （Tire）字典树

定义：又称单词查找树，Tire树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

• 3个基本性质：
  • 根节点不包含字符，除根节点外每一个节点都只包含一个字符；
  • 从根节点到某一节点路径上经过的字符连接起来，为该节点对应的字符串；
  • 每个节点的所有子节点包含的字符都不相同。

 

1. 海量数据找出前K大的数

top K类问题，通常比较好的方案是分治+Tire树/hash+小顶堆，即先将数据集按照Hash方法分解成多个小数据集，然后使用Trie树或者Hash统计每个小数据集中的query词频，之后用小顶堆求出每个数据集中出现频率最高的前K个数，最后在所有top K中求出最终的top K。

 

1. 2个2T文件qq号交集

2. 布隆过滤器（有两个文件，分别有20亿个QQ号（bigint类型，8字节），我们只有2G内存，如何找到两个文件交集？）

• 步骤1: 使用hash函数将第一个文件的所有整数映射到10个文件中，每个文件有2亿个整数，大约1600M内存，2G的内存就可以放下了，把10个文件记为a1,a2,....,a10;
• 步骤2：用同样的hash函数映射第二个文件到10个文件中，这10个文件记为b1,b2,b3,......,b10；
• 步骤3：由于使用的是相同的hash函数，所以两个文件中一样的数字会被分配到文件下标一致的文件中，分别对a1和b1求交集，a2和b2求交集，ai和bi求交集；
• 步骤4：最后将步骤3的结果汇总，即为两个文件的交集。

1. Bit位枚举

直接用bit位来枚举，假设QQ号最长11个号码，那么就是2^37的大小，就是用37位bit表示所有QQ。然后我们再对应每个37bit之外用2bit记录，第一个文件和第二个文件有没有

• 00 表示都没有
• 10 表示仅第一个文件有
• 01 同理仅第二个文件有
• 11 表示两个文件都有此QQ号

所以就是39个bit位，我们可以用一个int 32位，和一个char 8 位来一个记录

 

1. 海量数据排序——1TB的数据需要排序，但只有32GB的内存如何排序处理？

2. 把磁盘上的1TB数据分割为40块（chunks），每份25GB。（注意，要留一些系统空间！）
3. 顺序将每份25GB数据读入内存，使用quick sort算法排序。
4. 把排序好的数据（也是25GB）存放回磁盘。
5. 循环40次，现在，所有的40个块都已经各自排序了。（剩下的工作就是如何把它们合并排序！）
6. 从40个块中分别读取25G/40=0.625G入内存（40 input buffers）。
7. 执行40路合并，并将合并结果临时存储于2GB 基于内存的输出缓冲区中。当缓冲区写满2GB时，写入硬盘上最终文件，并清空输出缓冲区；当40个输入缓冲区中任何一个处理完毕时，写入该缓冲区所对应的块中的下一个0.625GB，直到全部处理完成。

• 优化

磁盘I/O通常是越少越好（最好完全没有），那么如何降低磁盘I/O操作呢？关键就在第5和第6步中的40路输入缓冲区，我们可以先做8路merge sort，把每8个块合并为1路，然后再做5-to-1的合并操作。

 

1. 五大查找方式

 

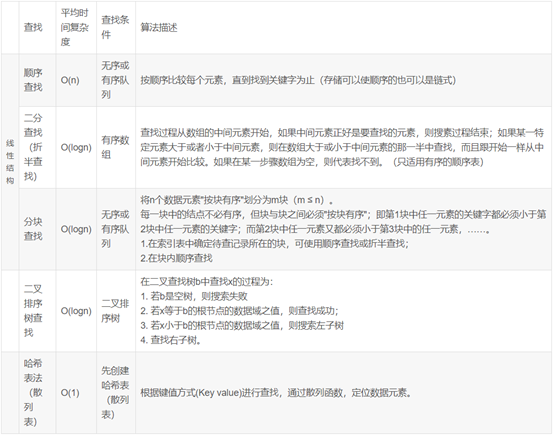
1. 常见搜索算法

• 广度优先搜索（BFS）：是一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以寻找结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。
  • 能够解决的问题：
    • 第一类问题：从节点A出发，有前往节点B的路径吗？
    • 第二类问题：从节点A出发，前往节点B的哪条路径最短？
  • 工作原理
    • Peggy既是Alice的朋友又是Bob的朋友，因此她将被加入队列两次：检查完一个人后，应将其标记为已检查，且不再检查他。

  

  • 算法实现：

import java.util.ArrayList;

import java.util.HashMap;

import java.util.List;

import java.util.concurrent.LinkedBlockingQueue;

 

public class BFS {

/**

* 打印出到达节点target所经过的各个节点信息

* @param target

*/

static void printSearPath(Node target) {

if (target != null) {

System.out.print("找到了目标节点:" + target.id + "\n");

 

List<Node> searchPath = new ArrayList<Node>();

searchPath.add(target);

Node node = target.parent;

while(node!=null) {

searchPath.add(node);

node = node.parent;

}

String path = "";

for(int i=searchPath.size()-1;i>=0;i--) {

path += searchPath.get(i).id;

if(i!=0) {

path += "-->";

}

}

System.out.print("步数最短："+path);

} else {

System.out.print("未找到了目标节点");

}

}

 

static Node findTarget(String startId,String targetId,HashMap<String,String[]> map) {

List<String> hasSearchList = new ArrayList<String>();

LinkedBlockingQueue<Node> queue=new LinkedBlockingQueue<>();

queue.offer(new Node(startId,null));

while(!queue.isEmpty()) {

Node node = queue.poll();

if(hasSearchList.contains(node.id)) {

continue;

}

System.out.print("判断节点:" + node.id +"\n");

if (targetId.equals(node.id)) {

return node;

}

hasSearchList.add(node.id);

if (map.get(node.id) != null && map.get(node.id).length > 0) {

for (String childId : map.get(node.id)) {

queue.offer(new Node(childId,node));

}

}

}

return null;

}

 

static class Node{

public String id;

public Node parent;

public Node(String id,Node parent) {

this.id = id;

this.parent = parent;

}

}

 

public static void main(String[] args) {

HashMap<String,String[]> hashMap=new HashMap<>();

hashMap.put("YOU",new String[]{"CLAIRE","ALICE","BOB"});

hashMap.put("CLAIRE",new String[]{"YOU","JONNY","THON"});

hashMap.put("JONNY",new String[]{"CLAIRE"});

hashMap.put("THOH",new String[]{"CLAIRE"});

hashMap.put("ALICE",new String[]{"YOU","PEGGY"});

hashMap.put("BOB",new String[]{"YOU","PEGGY","ANUJ"});

hashMap.put("PEGGY",new String[]{"BOB","ALICE"});

hashMap.put("ANUJ",new String[]{"BOB"});

Node target = findTarget("YOU","ANUJ",hashMap);

//打印出最短路径的各个节点信息

printSearPath(target);

}

}

• 深度优先搜索（DFS）：深度优先搜索是图论中的经典算法，利用深度优先搜索算法可以产生目标图的相应拓扑排序表，利用拓扑排序表可以方便的解决很多相关的图论问题，如最大路径问题等等。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。
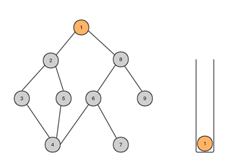
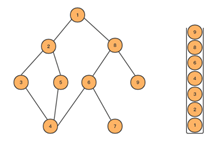
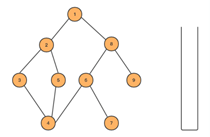
  • 对于下面的树而言，DFS方法首先从根节点1开始，其搜索节点顺序是1,2,3,4,5,6,7,8（假定左分枝和右分枝中优先选择左分枝）。

  

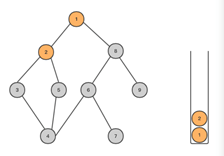
  • 从stack中访问栈顶的点；

  

  • 找出与此点邻接的且尚未遍历的点，进行标记，然后放入stack中，依次进行；

  

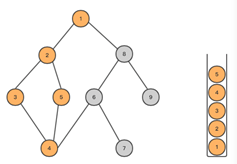
  • 如果此点没有尚未遍历的邻接点，则将此点从stack中弹出，再按照（3）依次进行；

  

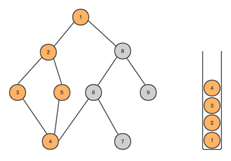
  • 直到遍历完整个树，stack里的元素都将弹出，最后栈为空，DFS遍历完成。

  

• 爬山法（Hill Climbing）：DFS的变形，不同的是每次选择的是最优的一个子结点，即局部最优解
  • 建立一个栈，将根结点放入栈
  • 判断栈顶元素是否是目标结点，如果是，算法结束，如果不是，进入第三步
  • 栈顶元素出栈，根据评估函数计算的顺序将此结点的子结点入栈
  • 如果栈空，则输出失败，否则，进入第二步
• 最佳优先算法（Best-first search strategy） ：是DFS和BFS的结合，每次找到的是所有结点中最好估计值的那个结点，找到的是全局最优解
  • 根据评估函数建立一个堆（或用优先队列），将根结点放入堆中
  • 判断栈顶元素是否是目标结点，如果是，算法结束，如果不是，进入第三步
  • 移出堆顶元素结点，将此结点的所有子结点加入堆
  • 如果堆空，输出失败，否则，进入第二步
• 回溯法 （Backtracking）：找到所有选择，走不通则回溯
  • 建立一个问题的部分解v=(a1,a2,...,ak)
  • 若这个部分解是可行解，则继续，若不是可行解，删除ak，加入ak情况的另一种可能
  • 若ak的可能已经遍历完，回溯并寻找ak-1的下一个可能
• 分支限界算法（Branch-and-bound Search Algorithm）：分支限界算法可以用来寻找最优解，在平均情况下不必穷尽搜索。用一种方法预测一系列解的最小界（lower bound），用一种方法预测最优解的最大界（upper bound）。如果一个解的最小界超出了整个解空间的最大界，那么这个解不可能是最优的，我们就可以提前终止此分支，分支界限适合最小化问题
• A*算法：对于优先队列，每取出一个结点n，将他的所有儿子结点n'放入优先队列，优先级由函数f(n)计算出

 

1. BFS、DFS优缺点

2. 深搜优缺点

• 优点
  • 能找出所有解决方案
  • 优先搜索一棵子树，然后是另一棵，所以和广搜对比，有着内存需要相对较少的优点
• 缺点
  • 要多次遍历，搜索所有可能路径，标识做了之后还要取消。
  • 在深度很大的情况下效率不高

1. 广搜优缺点

• 优点
  • 对于解决最短或最少问题特别有效，而且寻找深度小
  • 每个结点只访问一遍，结点总是以最短路径被访问，所以第二次路径确定不会比第一次短
• 缺点
  • 内存耗费量大（需要开大量的数组单元用来存储状态）

 

1. 动态规划

• 核心思想：将大问题分为小问题进行解决，从而一步步获得最优解的处理算法，与分治算法不同的是适合于动态规划求解的问题，经分解得到的子问题往往不是相互独立的。
• 求解方式：填表
• 思想：w[i]为第i个商品的重量，v[i]代表第i个商品的价值，v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值

1. v[i][0]=v[0][j]=0；//使得i和j刚好和第几个商品对应
2. 当w[i]>j时：v[i][j]=v[i-1][j]；//当准备加入新增的商品的容量w[i]大于当前背包的容量j时就直接使用上一单元格的装入策略
3. 当w[i]<=j时：v[i][j]=max{v[i-1][j]， v[i]+v[i-1][j-w[i]]}；

//上一个单元格的装入的最大值v[i-1][j]

//v[i]当前商品的价值

//v[i-1][j-w[i]]装入i-1个商品剩余空间j-w[i]的最大值

//根据前面得到公式来动态规划处理

for(int i = 1; i < v.length; i++) {//不处理第一行i是从1开始的

for(int j=1; j < v[0].length; j++){//不处理第一列，j是从1开始的

//公式

if(w[i-1]> j){//因为我们程序i是从1开始的，因此原来公式中的w[i]修改成w[i-1]

v[][j]=v[i-1][j];

}else{

//说明:

//因为我们的i从1开始的,因此公式需要调整成

//v[i][j]=Math.max(v[i-1][j],val[i-1]+v[i-1][j-w[i-1]]);

v[][j]=Math.max(v[i-1][j], val[i]+v[i-1][j-w[i-1]]);

}

}

}

 

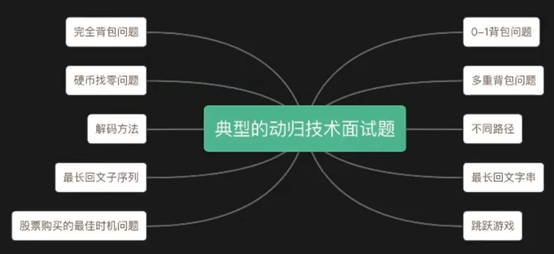
1. 什么样的题适合用动态规划？

• 最值型动态规划，比如求最大，最小值是多少
• 计数型动态规划，比如换硬币，有多少种换法
• 坐标型动态规划，比如在m*n矩阵求最值型，计数型，一般是二维矩阵
• 区间型动态规划，比如在区间中求最值

 

1. 暴力匹配算法

public static int ViolenceMatch(String str1， String str2) {

char[] s1 = str1.toCharArray()；

char[] s2 = str2.toCharArray()；

   

int i = 0；

int j = 0；

   

while (i < s1.length && j < s2.length) {

if (s1[i] == s2[j]) {

i++；

j++；

} else {

i = i - (j - 1)；

j = 0；

}

}

   

if (j == s2.length) {

return i - j；

}

   

return -1；

}

1.  

    

1. KMP算法

2. 建立部分匹配表

搜索词	A	B	C	D	A	B	D
部分匹配值	0	0	0	0	1	2	0

移动位数 = 已匹配的字符数 – 对应的部分匹配值

public static int[] KmpMatchTable(String str) {

int[] matchTable = new int[str.length()]；

matchTable[0] = 0；

for (int i = 1， j = 0； i < str.length()； i++) {

//不等时重新获取前一个的值，kmp算法核心

while (j > 0 && str.charAt(i) != str.charAt(j)) {

j = matchTable[j - 1]；

}

//部分匹配则值+1

if (str.charAt(i) == str.charAt(j)) {

j++；

}

matchTable[i] = j；

}

return matchTable；

}

   

1. KMP搜索

public static int KMPMatch(String str1， String str2) {

int[] matchTable=KmpMatchTable(str2)；

   

for (int i = 0，j=0； i < str1.length()； i++) {

//处理不等情况

while(j>0&&str1.charAt(i)!=str2.charAt(j)){

j = matchTable[j-1]；

}

   

if (str1.charAt(i)==str2.charAt(j)){

j++；

}

if (j==str2.length()){

return i-j+1；

}

}

   

return -1；

}

    

1. 贪心算法

• 概念：在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，它所做出的仅仅是在某种意义上的局部最优解。
• 基本思路
  • 建立数学模型来描述问题
  • 把求解的问题分成若干个子问题
  • 对每个子问题求解，得到子问题的局部最优解
  • 把子问题的解局部最优解合成原来问题的一个解
• 存在的问题
  • 不能保证求得的最后解是最佳的
  • 不能用来求最大值或最小值的问题
  • 只能求满足某些约束条件的可行解的范围

 

1. 普利姆算法（prim）

• 求最小生成树
• 普里姆算法介绍
  • 普利姆(Prim)算法求最小生成树，也就是在包含n个顶点的连通图中，找出只有(n-1)条边包含所有n个顶点的连通子图，也就是所谓的极小连通子图
  • 普利姆的算法如下:

1. 设G=(V,E)是连通网，T=(U,D)是最小生成树，V,U是顶点集合，E,D是边的集合
2. 若从顶点u开始构造最小生成树，则从集合V中取出顶点u放入集合U中，标记顶点v的visited[u]=1
3. 若集合U中顶点ui与集合V-U中的顶点vj之间存在边，则寻找这些边中权值最小的边，但不能构成回路，将顶点vj加入集合U中，将边（ui,vj）加入集合D中，标记visited[vj]=1
4. 重复步骤②，直到U与V相等，即所有顶点都被标记为访问过，此时D中有n-1条边
5. 提示：单独看步骤很难理解，我们通过代码来讲解，比较好理解.

 

1. 二叉树的中序遍历

List<Integer> list = new ArrayList<>()；

public TreeNode increasingBST(TreeNode root) {

if(null==root)return null；

Deque<TreeNode> queue = new ArrayDeque<>()；

while(root!=null||!queue.isEmpty()){

while(root!=null){

queue.add(root)；

root = root.left；

}

root = queue.pollLast()；

list.add(root.val)；

root=root.right；

}

return list；

}

 

1. 二叉树层序遍历

public List<List<Integer>> levelOrder(TreeNode root) {

List<List<Integer>> res = new ArrayList<>()；

Queue<TreeNode> queue = new ArrayDeque<>()；

if (root != null) {

queue.add(root)；

}

while (!queue.isEmpty()) {

int n = queue.size()；//记录节点个数

List<Integer> level = new ArrayList<>()；

//遍历每个节点的左右子节点

for (int i = 0； i < n； i++) {

TreeNode node = queue.poll()；

level.add(node.val)；

if (node.left != null) {

queue.add(node.left)；

}

if (node.right != null) {

queue.add(node.right)；

}

}

res.add(level)；

}

return res；

}

 

1. 二叉树之字形打印

public List<List<Integer>> zigzagLevelOrder(TreeNode root) {

List<List<Integer>> res = new ArrayList<>()；

if (root == null){

return res；

}

//创建队列，保存节点

Queue<TreeNode> queue = new LinkedList<>()；

queue.add(root)；//先把节点加入到队列中

boolean leftToRight = true；//第一步先从左边开始打印

while (!queue.isEmpty()) {

//统计这一层有多少个节点

int count = queue.size()；

//记录每层节点的值

List<Integer> level = new ArrayList<>()；

//遍历这一层的所有节点，把他们全部从队列中移出来，顺便

//把他们的值加入到集合level中，接着再把他们的子节点（如果有）

//加入到队列中

for (int i = 0； i < count； i++) {

//poll移除队列头部元素（队列在头部移除，尾部添加）

TreeNode node = queue.poll()；

//判断是从左往右打印还是从右往左打印。

if (leftToRight) {

//如果从左边打印，直接把访问的节点值加入到列表level的末尾

level.add(node.val)；

} else {

//如果是从右边开始打印，每次要把访问的节点值加入到列表的最前面

level.add(0， node.val)；

}

//左右子节点如果不为空会被加入到队列中

if (node.left != null){

queue.add(node.left)；

}

if (node.right != null){

queue.add(node.right)；

}

}

//把这一层的节点值加入到集合res中

res.add(level)；

//改变下次访问的方向

leftToRight = !leftToRight；

}

return res；

}

 

1. 判断A是否是B的子树

public class Solution {

//分为两个函数，一个用于遍历节点当做子树的根节点，

public boolean hasSubtree(TreeNode root1，TreeNode root2) {

if(root1==null||root2==null) return false；

//直接判断isSubTree(root1，root2)，并且采取||的方式确定结果。

return isSubTree(root1，root2)||hasSubtree(root1.left，root2)

||hasSubtree(root1.right，root2)；

}

//另一个用于判断是否是子树（必须要root2先空）

public boolean isSubTree(TreeNode root1，TreeNode root2){

if(root2==null) return true；

if(root1==null) return false；

if(root1.val==root2.val){

return isSubTree(root1.left，root2.left)&&

isSubTree(root1.right，root2.right)；

}else{

return false；

}

}

}

    

1. 最小硬币数

• 动态规划算法题：给定不同面额的硬币数组coins和总额amounts，求能够组成总额的最小硬币数。如coins=[1，2，5]，amounts=11，那么最少硬币数为5+5+1=3.

public static int CoinsChange(int[] coins， int amount， int coinSize) {

if (null == coins || amount == 0) return -1；

   

int[] temp = new int[amount + 1]；

for (int i = 0； i <= amount； i++) {

temp[i] = amount + 1；

}

temp[0] = 0；

for (int i = 1； i <= amount； i++) {

for (int j = 0； j < coinSize； j++) {

if (i >= coins[j]) {

temp[i] = Math.min(temp[i]， 1 + temp[i - coins[j]])；

}

}

}

return temp[amount] > amount ? -1 ： temp[amount]；

}

   

1. 二叉树反转左右子树

public class Solution {

public TreeNode InvertTree(TreeNode root) {

if(root == null){

return null;

}

TreeNode tmp = root.left;

root.left = InvertTree(root.right);

root.right = InvertTree(tmp);

return root;

}

}

 

1. 查找链表的倒数第k个节点

/**

*通过两个指针p1,p2，首先让p1往前走k-1步，然后让p1,p2一起往前走，当p1走到尾的时候，p2即为倒数第k个。总共走了n次。时间复杂度为O(n).

*/

public ListNode getKthFromEnd(ListNode head, int k) {

ListNode p1 = head;

ListNode p2 = head;

   

int temp=0;

while(p1.next!=null){

if(temp==k-1){

break;

}

p1=p1.next;

temp++;

}

   

while(p1.next!=null){

p1=p1.next;

p2=p2.next;

}

   

return p2;

}

 

1. 判断数组是否为搜索二叉树的后序遍历

二叉树的后序遍历：左孩子—>右孩子—> 父结点

• step1:如果一个数组arr是搜索二叉树的后序遍历结果，那arr的最后一个元素就是树的根结点root
• step2:去掉最后一个元素arr[End]=root后, arr可以分成两段，(前一段 = 左子树）小于root，(后一段 = 右子树)大于root
• step3: 分别递归前后两段，如果这（两段 = 子树）都是符合上述规则的。则输出true，否则输出false

public class verifySquenceOfBSTpostOrder {

    public boolean solve(int[] arr){

        if(arr == null || arr.length == 0){

            return true;

        }

        return judge(arr,0,arr.length-1);

    }

    

    boolean judge(int[] arr, int Start, int End){

        if(Start >= End){return true;}

         //找到，根节点位置

        int i = End ;

        //找到左右子树临界位置

        while (i > 0 && arr[i-1] > arr[End]){

            --i;

        }

        

        //判断左边部分是不是都小于根节点

        for( int j = i-1; j > 0; --j){

            if(arr[j] > arr[End])

             return false;

        }

        

        //分别递归左右子树

        return judge(arr, Start, i-1) && judge(arr, i, End-1);

    }

}

 

1. 删除链表中重复的元素（leetcode82）

public ListNode deleteDuplicates(ListNode head) {

if(head==null||head.next==null){

return head;

}

   

if(head.val==head.next.val){

ListNode move = head.next;

while(move!=null&&head.val==move.val){

move = move.next;

}

head = deleteDuplicates(move);

}else{

head.next = deleteDuplicates(head.next);

}

   

return head;

}