图的DFS遍历
2012-07-12 17:39 coodoing 阅读(781) 评论(0) 收藏 举报深度优先搜索(Depth-First Search—DFS)是指按照深度方向搜索,它类似于树的先根遍历,是树的先根遍历的推广
深度优先搜索连通子图的基本思想是:
假设图G初态为所有顶点未被访问(visited[i]=false),从G中任选一顶点vi :
- 从该顶点vi出发,首先访问vi,,置visited [vi ]=true;
- 然后依次搜索vi的每一个邻接点vj ;
- 若vj未被访问过,则以vj为新的初始出发点,重复1;若vj已被访问过,则返回到vi另一个邻接点,重复3
- 如果经过1、2、3后,图中仍有未被访问的顶点,再从中任选一顶点,重复1、2、3,直至所有顶点都被访问过,遍历结束。
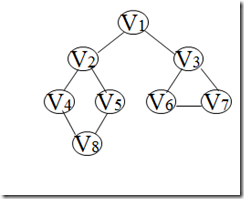
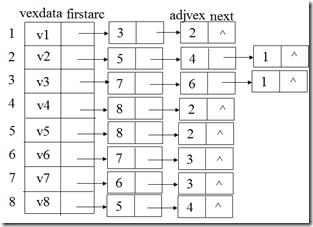
以无向连通图为例,其对应的邻接表为:
遍历过程如下:
令vi=v1
1. 访问 v1。
2. 求 vi的邻接点 vj。
3. 若vj未被访问过,则以vj为新的初始出发点,重复1
若vj已被访问过,则返回到vi另一个邻接点,重复3
其遍历结果为:
1: package Graph;
2:
3: public class DFSTest {
4:
5: int[] visited;
6: ALGraph graph = new ALGraph();
7:
8: private void createGraph(int[] vexs, int[][] arcs) {
9: graph.createGraph(vexs, arcs);
10: visited = new int[graph.vexNum];//new int[]{0};
11: }
12:
13: public void DFSTraversal(ALGraph graph, int v) {
14: for (int i = 0; i < graph.vexNum; i++)
15: visited[i] = 0;
16: System.out.println();
17: visited[v] = 1;
18: System.out.print(v + 1 + " ");
19: DFS(graph, v);
20: }
21:
22: private void DFS(ALGraph graph, int v) {
23: VNode node = graph.vertices.get(v);
24: ArcNode p = node.firstNode;
25: if (node != null)//遍历完以及v头结点对应的链表不为空
26: {
27: while (p != null) {
28: if (visited[p.vex - 1] == 0) {
29: System.out.print(p.vex + " ");
30: visited[p.vex - 1] = 1;
31: DFS(graph, p.vex - 1);
32: }
33: //System.out.println("next"+p.vex);
34: p = p.next;
35: }
36: } else {
37: return;
38: }
39:
40: }
41:
42: public static void main(String[] args) {
43: DFSTest dfs = new DFSTest();
44: int[] vexs = new int[5];
45: int[][] arcs = new int[2][];
46: // 初始化图
47: dfs.createGraph(vexs, arcs);
48:
49: ALGraph g = dfs.graph;
50: // 获取邻接表
51: g.getAdjList(g.vertices);
52:
53: // 从V1开始遍历
54: dfs.DFSTraversal(g, 0);
55: // 从V2开始遍历
56: dfs.DFSTraversal(g, 1);
57: }
58:
59: }



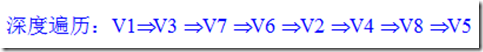

 浙公网安备 33010602011771号
浙公网安备 33010602011771号