强化学习Chapter3——贝尔曼方程

强化学习Chapter3——贝尔曼方程

上一节介绍了衡量回报 \(R\) 的相关函数，包括状态价值函数与动作价值函数，并且介绍了二者之间的等式关系

\[V^\pi(s)=E_{a\sim\pi}[Q^\pi(s,a)]=\sum_{a}\pi(a|s)Q^\pi(s,a)\\ Q^\pi(s,a)=r(s,a)+\gamma\sum_{s'}P(s'|s,a)V^\pi(s') \]

本节将通过这两个式子，导出贝尔曼方程

一、贝尔曼方程（Bellman equation）

根据 V 和 Q 的相互表示关系，可以预想到的是，从这两个式子可以导出类似动态规划的递归方程。下面将展示这个过程。

1、状态价值函数的贝尔曼方程

\[\begin{aligned} V^\pi(s)&=\sum_{a}\pi(a|s)Q^\pi(s,a)\\ &=\sum_{a}\pi(a|s)[r(s,a)+\gamma\sum_{s'}P(s'|s,a)V^\pi(s')]\\ &=\sum_{a}\pi(a|s)r(s,a)+\gamma\sum_{a}\pi(a|s)\sum_{s'}P(s'|s,a)V^\pi(s')\\ &=E_{a\sim \pi}[r(s,a)]+\gamma E_{a\sim\pi}[E_{s'\sim P}[V^\pi(s')]]\\ &=E_{a\sim\pi,s'\sim P}[r(s,a)+\gamma V^\pi(s')] \end{aligned} \]

为了突出时间线的递推性，也可以写成：

\[V^\pi(s_t)=E_{a\sim\pi,s_{t+1}\sim P}[r(s_t,a)+\gamma V^\pi(s_{t+1})] \]

其中 \(P\) 给定 \(s_t\) 和 \(a\) 的条件下，\(s_{t+1}\) 的分布。策略分布 \(\pi\) 与并不显式与 \(t\) 有关，毕竟大伙都只有一个脑子。

2、动作价值函数的贝尔曼方程

\[\begin{aligned} Q^\pi(s,a)&=r(s,a)+\gamma\sum_{s'}P(s'|s,a)V^\pi(s')\\ &=r(s,a)+\gamma\sum_{s'}P(s'|s,a)\sum_{a}\pi(a'|s)Q^\pi(s,a')\\ &=r(s,a)+\gamma\sum_{s'}P(s'|s,a)E_{a'\sim\pi}[Q(s,a')]\\ &=r(s,a)+\gamma E_{s'\sim P,a'\sim\pi}E[Q(s',a')]\\ &=E_{a'\sim \pi, s'\sim P}[r(s,a)+\gamma Q(s',a')] \end{aligned} \]

同理，也可以写成时间线的递推形式，此处不再赘述。可见，二者的形式其实十分相近。

二、贝尔曼最优方程（Bellman optimal equation）

即采用最优策略得到的 \(V\) 和 \(Q\) 的最值 \(V^*\) 和 \(Q^*\)，下面直接写出

\[V^*(s)=\max_a E_{s'\sim P}[r(s,a)+\gamma V^*(s')]\\ Q^*(s,a)=E_{s'\sim P}[r(s,a)+\gamma \max_{a'}Q^*(s',a')] \]

可以看到的是，这里“最优”的约束全在动作上，而动作是由策略决定，因此贝尔曼最优方程，其实是最优策略对应的贝尔曼方程。

三、向量形式

为了导出贝尔曼方程（BE）与贝尔曼最优方程（BOE），首先对 BE 公式进行重写：

\[V_\pi(s)=r_\pi(s)+\gamma\sum_{s'}P_\pi(s'|s)V_\pi(s')\\ \]

这里将策略 \(\pi\) 作为参数，简化贝尔曼方程。若将各值写成向量形式：

\[\begin{aligned} &V_\pi = [V_\pi(s_1),...,V_\pi(s_n)]^T\in \R^n\\ &r_\pi = [r_\pi(s_1),...,r_\pi(s_n)]^T\in \R^n\\ \\ &P_\pi\in R^{n\times n}\ \ where\ [P_\pi]_{ij}=p_\pi(s_j|s_i) \end{aligned} \]

就能得出向量形式的贝尔曼方程：

\[V_\pi=r_\pi+\gamma P_\pi V_\pi \]

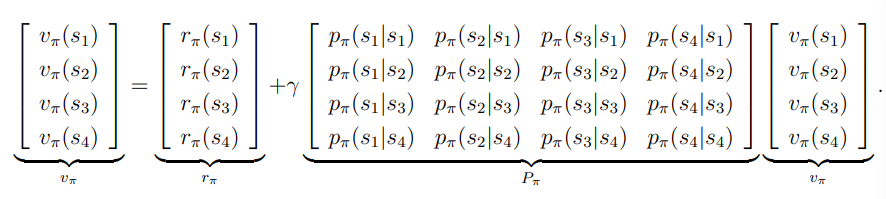
向量形式极大简化了贝尔曼公式，如此简洁精炼，大大简化了相关公式的证明。同时这也给解贝尔曼方程提供了思路。

\[V_\pi=(I-\gamma P_\pi)^{-1}r_\pi \]

通过矩阵运算，能够在给定 \(P_\pi,r_\pi\) 的条件下（所有状态切换信息透明），求出给定策略的状态价值函数 \(V_\pi\). 上式可直接导出下面的几个性质：

• 由于 \(P_\pi\) 半正定，有 \((I-\gamma P_\pi)^{-1}=I+\gamma P_\pi+\gamma^2 P_\pi^2+...\ge I\ge 0\)，所以 \(if\ r\ge 0, then\ (I-\gamma P_\pi)^{-1}r\ge r\ge 0\).
• \(if\ r_1\ge r_2,then\ (I-\gamma P_\pi)^{-1}r_1\ge (I-\gamma P_\pi)^{-1}r_2\)，即 \(v_1\ge v_2\).

由于基于矩阵求逆的算法求解贝尔曼方程，对信息需求苛刻，在某些复杂情况下可用性十分有限，因此更多寻找最优策略的算法被逐渐提出。

Reference：

• Mathematical Foundations of Reinforcement Learning. https://github.com/MathFoundationRL