自注意力机制

自注意力机制

O、前置知识——单词向量编码

在文字处理中，我们对单词进行向量编码通常有两种方式：

1. 独热编码(one-hot encoding)：用N位的寄存器对N个状态编码，通俗来讲就是开一个很长很长的向量，向量的长度和世界上存在的词语的数量是一样多的，每一项都表示一个词语，只要把其中的某一项置1，其他的项都置0，那么就可以表示一个词语，但这样的编码方式没有考虑词语之间的相关性，并且内存占用也很大

2. 词向量编码(Word Embedding)：将词语映射(嵌入)到另一个数值向量空间，可以通过向量空间内的距离（如点积）来表征不同词语之间的相关性。

独热编码的方式，基本被遗弃了，通过一个线性层，将一个单词映射为一个词向量，成为目前 LLM(Large Language Model) 主流的做法。

一、注意力机制

深度学习中的注意力机制通常可分为三类：软注意（全局注意）、硬注意（局部注意）和自注意（内注意）

1. Soft/Global Attention(软注意机制)：对每个输入项的分配的权重为0-1之间，也就是某些部分关注的多一点，某些部分关注的少一点，因为对大部分信息都有考虑，但考虑程度不一样，所以相对来说计算量比较大。

2. Hard/Local Attention(硬注意机制)：对每个输入项分配的权重非0即1，和软注意不同，硬注意机制只考虑那部分需要关注，哪部分不关注，也就是直接舍弃掉一些不相关项。优势在于可以减少一定的时间和计算成本，但有可能丢失掉一些本应该注意的信息。

3. Self/Intra Attention（自注意力机制）：对每个输入项分配的权重取决于输入项之间的相互作用，即通过输入项内部的"表决"来决定应该关注哪些输入项。和前两种相比，在处理很长的输入时，具有并行计算的优势。

二、自注意力机制

理解自注意力机制的关键在于，理解Q、K、V机制计算加权的方法。该部分应当了解四个矩阵 \(W^q,W^k,W^v,W^o\).

1、自注意力机制的目标

注意力机制的最本质的思路是 “加权”，不论是软注意力还是硬注意机制，都是在输入模型真正逻辑结构之前，为输入的系列词向量加上权重。而自注意力机制，同样如此。下图是自注意力机制的目标：

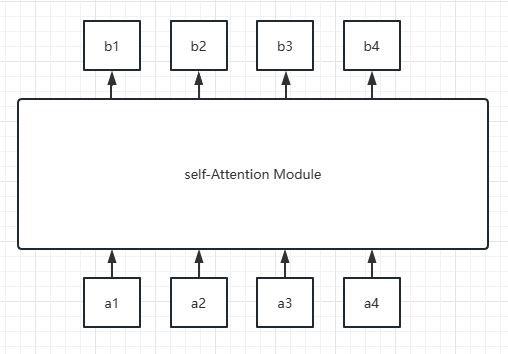
即有一系列词向量 \(\{a_i\}\)，输出的 \(\{b_i\}\) 为各个词向量的加权结果：

\[\begin{equation} b_j=\sum_iw^j_ia_i \end{equation} \]

可以看出，此处的权重 \(w^j_i\) 并不固定，还与 \(b_j\) 的位置 \(j\) 有关。这是区别于软注意力和硬注意力机制最显著的地方，从现实情况看，所谓关注上下文的信息，也并不是关注上下文固定位置的信息，而是动态的观察周围单词的信息。

2、自注意力的 Q、K、V

自注意力机制，首先引出了三个矩阵：\(W^q,W^k,W^v\).

矩阵	计算
\(W^q\)：query 矩阵	\(q_i=W^qa_i\)
\(W^k\)：key 矩阵	\(k_i=W^ka_i\)
\(W^v\)：value 矩阵	\(v_i=W^va_i\)

可以看出，三个矩阵分别与输入的单词向量相乘，获得对应的 q,k,v 向量。下面直接给出解释：

• \(q_i\) 向量：作为 \(a_i\) 的 query 向量，用于与每个词向量 \(a_j\) 的 key 向量相乘，获得相关性常数 \(\alpha_{i,j}\)
• \(k_i\) 向量：作为 \(a_i\) 的 key 向量，用于被每个词向量的 query 向量相乘。
• \(v_i\) 向量：作为 \(a_i\) 的 value 向量，用于表征 \(a_i\) 的内容信息，同时也是 \(b_i\) 的加权对象。

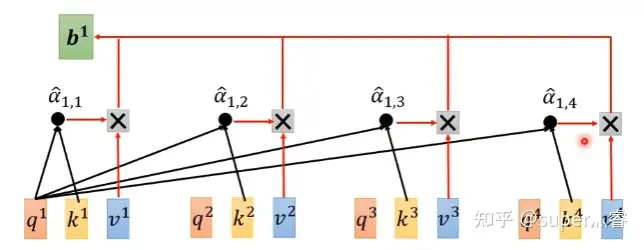
结合该图，可以很清晰的看出自注意力机制的计算过程（这里以计算 \(b_1\) 为例）：

• 将向量 \(a_1\) 的 query 向量与每个词向量的 key 向量相乘得到相关性得分
• 对所有相关性得分 \(\alpha_i\) 归一化
• 对向量 \(a_i\) 的 value 向量使用相关性得分归一化的结果加权，得到 \(b_1\) 向量

总的来说，自注意力机制基本完成了前文所述的目标，不过加权的并不是 \(a_i\) 而是其 value 向量。所谓自注意力，其实从 \(q,k,v\) 三个向量的计算可以看出，都是从 \(a_i\) 得来，这也是称之为自注意力的缘由。除此之外，具体到计算过程中，q、k、v向量的计算是可以并行的，即可以对多个单词向量 \(a_i\) 同时计算其 \(q_i,k_i,v_i\) ，因此实际上计算的是 \(Q,K,V\) （\(q_i,k_i,v_i\) 计算的结果矩阵）。

3、多头自注意力

多头自注意力引出了 \(W^o\) .

从自注意力矩阵的思路，是利用了三个矩阵，将 \(a_i\) 映射到不同的子空间中，并分别得到有用的 \(q,k,v\) 向量。多头自注意力的想法是，仅仅单个的 \(q,k,v\) 并不能将 \(a_i\) 所在的空间信息完全的表达出来，因此对于每一个词向量 \(a_i\) 都应用多个 \(W^q,W^k,W^v\) （原论文中为 8 个），同时并行进行上述的 \(q,k,v\) 操作。

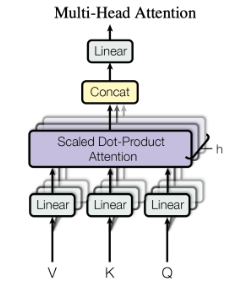
这就使得最终的输出有 8 个矩阵，但是输给前馈层仅需要一个矩阵就行，所以这里将这 8 个结果进行 concat，强行连接成为一个矩阵。为了契合维数的要求，在 concat 之后，将这个 “长长” 的矩阵进行投影，即乘以一个 \(W^o\) 将其压缩到需要的维度。这就是 \(W^o\) 的由来。

多头自注意力的思路，提高了模型关注不同位置的能力，因为 8 个头所关注的位置并不完全相同，提高了模型的鲁棒性。同时也为注意力层提高了多个“表示子空间”，能够更加充分的表征单词的距离、内容等信息。它也增加了模型的参数量，从而能够容纳更多信息。

这部分之后准备融到 transformer 论文的阅读里去~