题解 P1073 【最优贸易】
首先,SPFA大法没死!!!
步入正题
开始
因为我刚学完最短路没多久(所以这应该会是一篇对新手比较友好的题解QAQ),这题涉及到了费用问题所以可以考虑最短路,但是我只会Floyd,dijkstra还有SPFA,但是一想到买和卖,当然是一个正数一个负数,于是果断选择SPFA(课上说一有负权边就用SPFA,QAQ)
核心思想
引入
课上讲了这道题的大概轮廓,核心思想是分层图,
通俗来讲就是把不同的状态用不同层的图来表达
感觉其实点都不通俗,举个例子,一道简单的求最短路的题目,它硬是加上了某些花里胡哨的条件,让你不能那么顺利的求最短路,这时就可以将限制条件转变成某种状态并单独作为一层图
就比如这题,本来可以是一个旅者找前往某个城市的最短路劲,但是它又加上了balabala水晶球贸易水晶球什么的,还要你求最大收益。
可能可能很容易想到建一张图,用城市与城市之间的权值来表示,但试问如何用一条边来选择购买,出售,还是直接路过呢?
假如旅行者一开始有一个面包,沿途经过某个城市需要吃一定量的面包,这时上述的做法就很方便了,将吃的面包量作为权值求最短路。
但是这里则不然,这时分层图的优势就体现出来了——将不同状态分别作为一张图。
实操
首先我用一组乱打的简单的数据来举例
3 3
3 4 5
1 2 1
1 3 1
2 3 1
建图(邻接表)
关于层
因为题目说只会买卖一次,所以我们可以将什么都没有作为一层,购买了水晶球作为一层,出售了水晶球作为一层,再考虑到是先购买再出售,我们可以将它们向下分别作为1,2,3层(顺序不重要)。
如下
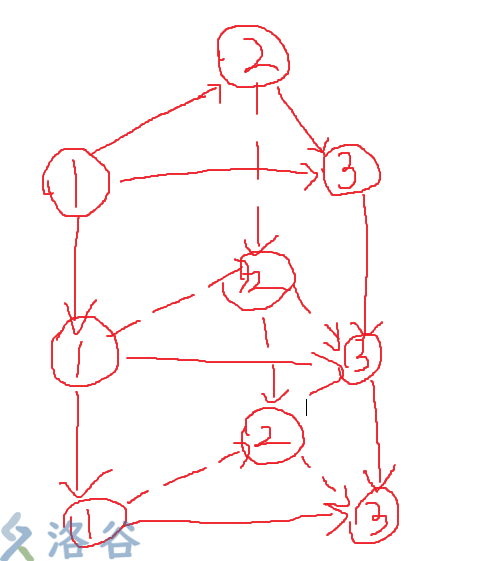
我们将跨层的操作对应到状态的变化或转移,也就是从第一层到第二层就是购买,第二层到第三层就是出售。
代码实现
void ins_self(int node,int val){
G[node].push_back(make_edge(node+n,-val));
G[node+n].push_back(make_edge(node+2*n,val));
}
for (int i = 1; i <= n; i++) {
cin>> v[i];
ins_self(i,v[i]);
}
//在一开始输入数据的时候就可以完成层之间的连通
//G[N]是用于存图的,n是城市的数量,v[i]是不同城市的标价
//make_edge函数是将某条边的终点和边权打包成结构体以方便存入G[N]中
//N是某个常数
关于边
实现的方式还是利用边的权值,我们在层与层之间连边,对应的权值就是到某个城市购买或出售的费用。
例如我要在一号城市购买,那么只需要从第一层的一号点走向第二层的一号点,用某种手段(一个记录点i到起点距离的数组dis[ i ])来记录权值的变化。另外由于移动不需要费用,所以层内部边之间的边权都是0。
代码实现
void ins(int node,int next,int val) {
G[node].push_back(make_edge(next,val));
G[node+n].push_back(make_edge(next+n,val));
G[node+2*n].push_back(make_edge(next+2*n,val));
}
//层内部的点之间的建边
for (int i = 1; i <= l; i++) {
cin>> a>> b>> c;
if (c == 1)
ins(a,b,0);
else if (c == 2) {
ins(a,b,0);
ins(b,a,0);
}
}
// l 是道路的数量,也就是边的数量
关于点
在这里并不需要真的去建三张图,而是给不同层点以不同的编号,直接举例就很容易明白的了
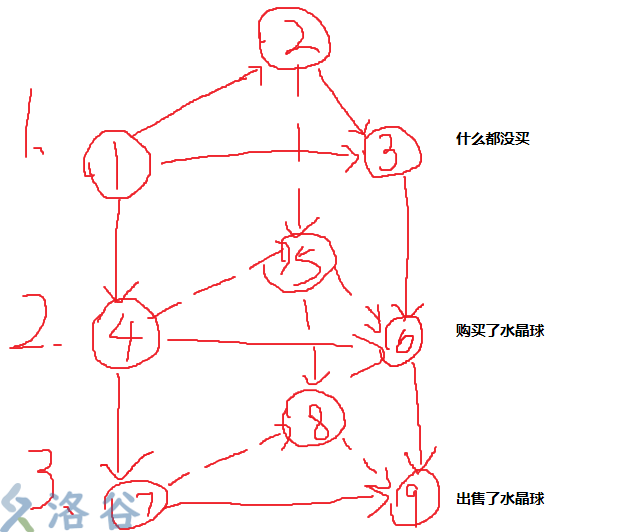
每一层图的节点编号就是它上一层对应的点的编号加上点的个数。
SPFA的实现
很明显我们希望在从第一层到第二层的时候边权能尽量小,第二到第三层的边权能尽量大,那这样我们就需要求出1号点到9号点的最长路就好了!
可是我没学过最长路QAQ(后来发现最长路好像更简单),于是,重点!精髓!我开了个脑洞,能否把买当作卖,把卖当作买,把一开始没有变成一开始有,目的是在途中以廉价卖掉,最后高价购买,这样原来赚的钱最多,反过来之后不久变成了亏的钱最多吗!比如我的例子中显然最赚是,1点买3点卖,赚两块钱,要是反过来,1点卖,3点买,那么就是亏了两块,正好就是原正解的相反数!
这样就完美的解决了最短路的问题,就可以直接把模板复制上去了,这里附上我的模板
代码实现
queue<int> Q;
int spfa(int ed){
Q.push(1);
inq[1] = true;
memset(dis,0x3f,sizeof(dis));
dis[1] = 0;
while (!Q.empty()){
int now = Q.front();
Q.pop();
inq[now] = false;
for (int i = 0;i < G[now].size();i++){
edge e = G[now][i];
if (dis[e.next]>dis[now]+e.val){
dis[e.next] = dis[now] + e.val;
if (inq[e.next] == false) {
Q.push(e.next);
inq[e.next] = true;
}
}
}
}
return dis[ed]==INF ? 0 : dis[ed];
}
最后
最后输出spfa(3*n),也就是1号城市经过购买和出售两步操作后到n号城市(对应第三层的3n号)的结果的的相反数就好了!!!没了!!!
结尾
用了这么一种诡异的做法还是有点心虚的,看到这么多dalao的神奇做法,还是打算学习一下,改进改进,希望这篇题解能帮到一些像我一样刚学的小白QAQ,最后我的代码附上(时间和空间好像都不是很好的亚子)。
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 210011;//这里不知道为什么不能是200011,有dalao看到求教教怎么定数组大小QAQ
const int INF = 0x3f3f3f3f;
int n,l,v[N];//节点,边数 ,权值
int dis[N];
bool inq[N];
struct edge {
int next,val;
};
vector<edge> G[N];
edge make_edge(int next, int val) {
edge cum;
cum.next=next;
cum.val=val;
return cum;
}
void ins(int node,int next,int val) {
G[node].push_back(make_edge(next,0));
G[node+n].push_back(make_edge(next+n,0));
G[node+2*n].push_back(make_edge(next+2*n,0));
}
void ins_self(int node,int val){
G[node].push_back(make_edge(node+n,val));
G[node+n].push_back(make_edge(node+2*n,-val));
}
queue<int> Q;
int spfa(int ed){
Q.push(1);
inq[1] = true;
memset(dis,0x3f,sizeof(dis));
dis[1] = 0;
while (!Q.empty()){
int now = Q.front();
Q.pop();
inq[now] = false;
for (int i = 0;i < G[now].size();i++){
edge e = G[now][i];
if (dis[e.next]>dis[now]+e.val){
dis[e.next] = dis[now] + e.val;
if (inq[e.next] == false) {
Q.push(e.next);
inq[e.next] = true;
}
}
}
}
return dis[ed]==INF ? 0 : dis[ed];
}
int main(void) {
int a,b,c;
cin>> n>> l;
for (int i = 1; i <= n; i++) {
cin>> v[i];
ins_self(i,v[i]);
}//自己建自己(层与层)
for (int i = 1; i <= l; i++) {
cin>> a>> b>> c;
if (c == 1) {
ins(a,b,0);
}
else if (c == 2) {
ins(a,b,0);
ins(b,a,0);
}//自己建别人(层内部)
}
spfa(3*n);
cout << -dis[n*3]<<endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号