动态规划之0-1背包问题

动态规划之0-1背包问题

---

1. 问题描述

​ 给定\(n\)件物品和一背包，物品\(i\)的重量是\(w_i\)，其价值为\(v_i\)，背包的容量为\(c\)。问应如何选择装入背包中的物品，使得装入背包中物品的总价值最大？
​ 在选择装入背包的物品时，对于每种物品\(i\)只有俩种选择，即装入背包或不装入背包。不能将物品\(i\)装入背包多次，也不能只装入部分的物品\(i\)，该问题称为0-1背包问题。即价值和重量数组中只能是整数。

2.问题分析

​ 该问题具有最优子结构的性质，符合动态规划的前提。主要看该问题的递归关系：
​ \(k\)表示为第k件物品，\(j\)表示当前背包剩余容量，\(B(k, j)\)表示前\(k\)件物品装入容量为\(j\)的背包时，背包中此时的价值，\(value_k\)表示物品\(k\)的价值，\(weight_k\)表示物品\(k\)的重量

\[B(k, j) = \begin{cases} B(k - j, j) &\text value_k > j \quad ① \\ \max\{B(k - 1, j), B(k - 1, j - w_k) + v_k\} &\text value_k \le j \quad ② \\ \end{cases} \]

​ 即有当决定物品\(k\)是否装入时有以下俩种情况：

• 当前物品重量大于背包剩余重量时：直接考虑这个物品不加入，继续计算前一个物体加入时的价值

• 当前物品重量小于等于背包剩余重量时：分别计算第\(k\)件物品加入背包时的价值\(B(k - 1, j - w_k) + v_k\)和第\(k\)件物品不加入背包时的价值\(B(k - 1, j)\)，将较大的值赋给当前的\(B(k, j)\)

  解决该问题实际上就是填写下面的表格的过程：

  

  

3.代码分析

​ 所用变量：

/**
 * N        表示物品的数目 + 1
 * C        表示背包容量 + 1 
 * weight   存储物品重量数组
 * value    存储物品价值数组
 * B        存储各个时刻的最优解
 **/
#define N 11
#define C 35

int weight[N] = {0, 4, 5, 7, 2, 8, 3, 9, 6, 1, 10};
int value[N] = {0, 25, 14, 15, 4, 14, 5, 14, 8, 1, 10};
int B[N][C] = {0};

​ 核心计算代码：
​ 计算最优解函数：

void knapsack() {
    int i, j;
    for (i = 1;i < N;i++) {
        for (j = 1;j < C;j++) {
            if (weight[i] > j) {
                // 等价于递推式①
                B[i][j] = B[i - 1][j];
            } else {
                // 等价于递推式②
                int value1 = B[i - 1][j - weight[i]] + value[i];
                int value2 = B[i - 1][j];
                B[i][j] = value1 > value2 ? value1 : value2;
            }
        }
    }
}

​ 构造最优解函数：

/**
 * matrix   记录最优解二维数组
 * n        物品数目
 * j        背包容量
 * 
 * 从最优解最后一行，即最后一个物品向前推算
 * 若未加入当前物品和加入当前物品的总价值一样，则表示当前物品不加入背包，即x[i] = 0
 * 否则当前物品需要加入背包(x[i] = 1)，且将当前背包容量j修改为加入当前物品后的状态(j -= weight[i])
 **/
void TraceBack(int (*matrix)[C], int n, int j) {
    for (int i = n; i > 0; i--) {
        if (matrix[i][j] == matrix[i - 1][j]) {
            x[i] = 0;
        } else {
            x[i] = 1;
            j -= weight[i];
        }
    }
}

4. 完整代码

/**
 * 0-1背包问题
 * 递推式
 **/
#include "stdio.h"
#include "stdlib.h"

/**
 * N        表示物品的数目 + 1
 * C        表示背包容量 + 1 
 * weight   存储物品重量数组
 * value    存储物品价值数组
 * B        存储各个时刻的最优解
 * x        存储物品选择信息
 **/
#define N 11
#define C 35

int weight[N] = {0, 4, 5, 7, 2, 8, 3, 9, 6, 1, 10};
int value[N] = {0, 25, 14, 15, 4, 14, 5, 14, 8, 1, 10};
// int weight[N] = {0, 9, 3, 4, 5, 2};
// int value[N] = {0, 10, 4, 5, 8, 3};
int B[N][C] = {0};
int article[N] = {0};
int x[N];

void print_matrix(int (*matrix)[C], int i, int j) {
    for (int a = 0;a < i;a++) {
        for (int b = 0;b < j;b++)
            printf("%-4d", matrix[a][b]);
        printf("\n");
    }
}

void knapsack() {
    int i, j;
    for (i = 1;i < N;i++) {
        for (j = 1;j < C;j++) {
            if (weight[i] > j) {
                B[i][j] = B[i - 1][j];
            } else {
                int value1 = B[i - 1][j - weight[i]] + value[i];
                int value2 = B[i - 1][j];
                B[i][j] = value1 > value2 ? value1 : value2;
            }
        }
    }
    print_matrix(B, N, C);
}

void TraceBack(int (*matrix)[C], int n, int j) {
    for (int i = n; i > 0; i--) {
        if (matrix[i][j] == matrix[i - 1][j]) {
            x[i] = 0;
        } else {
            x[i] = 1;
            j -= weight[i];
        }
    }
}

int main(int argc, char const *argv[]) {
    knapsack();
    printf("%d\n", B[N - 1][C- 1]);
    TraceBack(B, N - 1, C - 1);
    for (int i = 1; i < N; i++)
        printf("%d ", x[i]);
    printf("\n");
    system("pause");
    return 0;
}

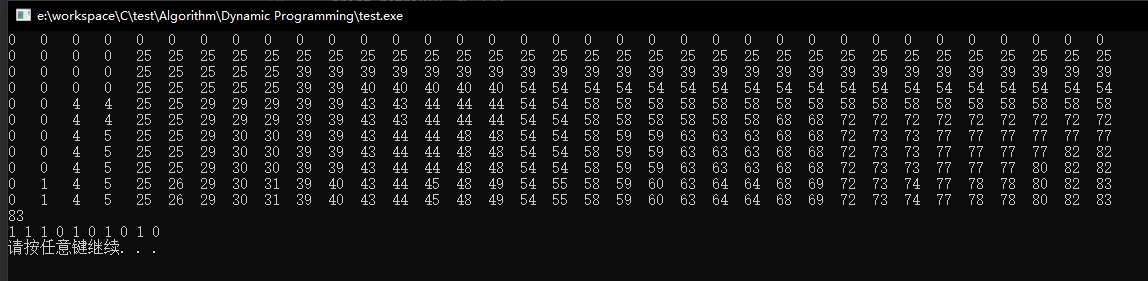
5.运行结果

​ 其中前面的二维数组为最优解的记录数组B中的值，\(83\)为最优解，下面的一维数组表示物品的是否装入的状态，\(1\)表示装入，\(0\)表示不装入
​