回溯法的总结

回溯法的总结

---

​ 回溯法的解空间树主要包含\(n\)叉树、排列树、子集树。

​ 例如在回溯法求解\(N\)皇后问题时，采用\(n\)叉树的结构，如下图所示：
​

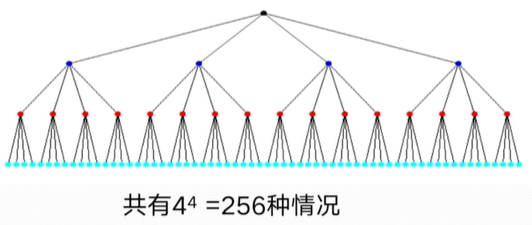
​ 该解空间即为\(n\)叉树的情况，当\(x_1\)选择\(1\)时，即进入第一个分支，进而在通过剪枝函数判断，当前分支是否有可能为最优解，若为可能产生最优解则展开第一个分支；若不可能，则剪去该分支。依次递归下去对\(x_2, x_3, ...\)分别求解，当到达最后树的叶子结点，即表示这种情况可行，就可以进行后续操作，包括保存路径或保存最优解等。
​ 当一条分支执行完毕后，退出当前递归，即返回上一层的状况，这就需要我们将进入分支时，对数据的修改撤回，体现在BackTrack1(t + 1);代码前后的对称性。这样就能确保从第一条分支递归结束，返回根节点再执行第二条分支时，数据恢复到根节点最初的数据。
​ 最大团问题求解时，该特点明显，如下：

void BackTrack(int i) {
    if (i > n) {
        for (int j = 1; j <= n; j++)
            bestx[j] = x[j];
        bestn = cn;
        return ;
    }
    int ok = 1;
    for (int j = 1; j < i; j++)
        if (x[j] == 1 && a[i][j] == 0) {
            ok = 0;
            break;
        }
    if (ok) {
        x[i] = 1;
        cn++;
        BackTrack(i + 1);
        cn--;
    }
    if (cn + n - i > bestn) {
        x[i] = 0;
        BackTrack(i + 1);
    }
}

​ 可以发现在\(17\)行中BackTrack(i + 1);的前后代码是对称的，cn++在退出递归时，进行了cn--撤销了对cn的操作。而x[i] = 1;由于每次递归时都需要重新赋值，因此无需写出其对称代码。
​ 9~13行即为剪枝函数，将结点与已成团的结点不相连的分支直接剪去，不进行递归访问，提高搜索效率。20~23为限界函数，要求右子树中，剩下的所有结点数和以及抱团的结点数大于当前最优解数，这样才有可能有更好的解，进行递归访问，

​ 总得来说，回溯法主要是遍历问题的所有可行解，将所有的解构成树的解空间，在通过剪枝函数和限界函数，剪去错误的分支，降低无效的搜索，以此提高搜索效率。