回溯法之图的m着色问题
回溯法之图的m着色问题
1. 问题描述
给定无向连通图\(G\)和\(m\)种不同的颜色。用这些颜色为图\(G\)的各个顶点着色,每个顶点着一种颜色。是否有一种着色发使\(G\)中每条边的2个顶点着不同颜色。这个问题是图的\(m\)可着色判定问题。若一个图最少需要\(m\)种颜色才能使图中每条边链接的2个顶点着不同颜色,则称这个数\(m\)为该图的色数。求一个图的色数\(m\)的问题称为图的\(m\)可着色优化问题。
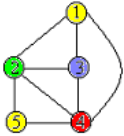
2.问题分析
本问题只探讨对于给定的\(m\),求解其可\(m\)着色的方案数
解向量:\((x_1, x_2, ..., x_n)\)表示顶点\(i\)所着颜色\(x_i\)
可行性约束函数:顶点\(i\)与已着色的相邻顶点颜色不重复
3.代码求解
使用变量:
/**
* n 国家数
* m 可用颜色数
* a 图的邻接矩阵
* x 当前解
* sum 着色方案数
**/
int n = MAX;
int 0m;
int a[MAX + 1][MAX + 1] = {
{0, 0, 0, 0, 0, 0},
{0, 0, 1, 1, 1, 0},
{0, 1, 0, 1, 1, 1},
{0, 1, 1, 0, 1, 0},
{0, 1, 1, 1, 0, 1},
{0, 0, 1, 0, 1, 0}
};
int x[MAX + 1];
long sum = 0;
核心代码:
// ok约束函数
// 要求a[k][j] == 1即俩顶点相邻
// x[j] == x[k]即二者的颜色重复
// 当二者都满足时,即该节点不符合剪枝函数,剪去
int ok(int k) {
for (int j = 1; j < k; j++)
if (a[k][j] && (x[j] == x[k]))
return 0;
return 1;
}
// t > n代表一种着色方案通过
// 通过遍历m,对各个结点设置不同的颜色
// 然后通过剪枝函数,只留下相邻顶点颜色不重复的分支,继续递归求解
void BackTrack(int t) {
if (t > n)
sum++;
else
for (int i = 1; i <= m; i++) {
x[t] = i;
if (ok(t))
BackTrack(t + 1);
}
}
4. 完整代码
/**
* 回溯法之图的n着色问题
**/
#include <stdio.h>
#include <stdlib.h>
#define MAX 5
/**
* n 国家数
* m 可用颜色数
* a 图的邻接矩阵
* x 当前解
* sum 着色方案数
**/
int n = MAX;
int m;
int a[MAX + 1][MAX + 1] = {
{0, 0, 0, 0, 0, 0},
{0, 0, 1, 1, 1, 0},
{0, 1, 0, 1, 1, 1},
{0, 1, 1, 0, 1, 0},
{0, 1, 1, 1, 0, 1},
{0, 0, 1, 0, 1, 0}
};
int x[MAX + 1];
long sum = 0;
// ok约束函数
// 要求a[k][j] == 1即俩顶点相邻
// x[j] == x[k]即二者的颜色重复
// 当二者都满足时,即该节点不符合剪枝函数,剪去
int ok(int k) {
for (int j = 1; j < k; j++)
if (a[k][j] && (x[j] == x[k]))
return 0;
return 1;
}
// t > n代表一种着色方案通过
// 通过遍历m,对各个结点设置不同的颜色
// 然后通过剪枝函数,只留下相邻顶点颜色不重复的分支,继续递归求解
void BackTrack(int t) {
if (t > n)
sum++;
else
for (int i = 1; i <= m; i++) {
x[t] = i;
if (ok(t))
BackTrack(t + 1);
}
}
void main() {
m = 3;
BackTrack(1);
printf("%d\n", sum);
system("pause");
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号