回溯法之最大团问题

回溯法之最大团问题

---

1. 问题描述

​ 给定无向图\(G = (V, E)\)。如果\(U \subseteq V\)，且对任意\(u, v \in U\)，有\((u, v) \in E\)，则称\(U\)是\(G\)的完全子图。
​ 完全子图\(U\)是\(G\)的团\(\iff\)不包含在比\(G\)更大的完全子图中。
​ \(G\)的最大团是指在\(G\)中所含顶点数最多的团。
​

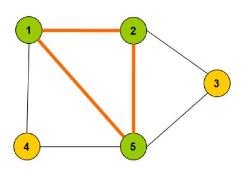
2.问题分析

​ 设当前扩展节点\(Z\)位于解空间树的第\(i\)层。在进入左子树前，必须确认从顶点\(i\)到已选入的顶点集中每个顶点都有边相连。在进入右子树前，必须确认还有足够多的可选顶点，使得算法有可能在右子树中找到更大的团。
​ 解空间：子集树
​ 可行性约束函数：\(x[j] == 1 \&\& !a[i][j]\)，顶点\(i\)到已选入的顶点集中每一个顶点都有边相连
​ 上界函数：\(cn + n - i > bestn\)，即以选择的结点数加上剩下的结点数需大于当前最优解的结点数

3. 代码求解

​ 使用变量：

/**
 * a    图G的邻接矩阵
 * n    图G的顶点数
 * x    当前解
 * bestx当前的最优解
 * cn   当前顶点数
 * bestn当前最大顶点数
 **/
int a[MAX + 1][MAX + 1] = {
    {0, 0, 0, 0, 0, 0},
    {0, 0, 1, 0, 1, 1},
    {0, 1, 0, 1, 0, 1},
    {0, 0, 1, 0, 0, 1},
    {0, 1, 0, 0, 0, 1},
    {0, 1, 1, 1, 1, 0}
};
int n = MAX;
int x[MAX + 1] = {0};
int bestx[MAX + 1];
int cn;
int bestn;

​ 核心代码：

// i > n 表示找到当前的最优解，将路径保存到bestx数组，将顶点数保存到bestn
// 设置标志变量ok，标识可行性约束函数的结果，ok = 1即表示当前节点可以加入到结果集中
// 对于通过约束函数的结点访问其左子树，并将当前结点添加到路径中，并++结点数
// 再进行上界函数讨论，即访问结点右子树，当右子树中有足够多的结点构成更大的团时，访问右子树
void BackTrack(int i) {
    if (i > n) {
        for (int j = 1; j <= n; j++)
            bestx[j] = x[j];
        bestn = cn;
        return ;
    }
    int ok = 1;
    for (int j = 1; j < i; j++)
        if (x[j] == 1 && a[i][j] == 0) {
            ok = 0;
            break;
        }
    if (ok) {
        x[i] = 1;
        cn++;
        BackTrack(i + 1);
        cn--;
    }
    if (cn + n - i > bestn) {
        x[i] = 0;
        BackTrack(i + 1);
    }
}

4.完整代码

#include <stdio.h>
#include <stdlib.h>

#define MAX 5

/**
 * a    图G的邻接矩阵
 * n    图G的顶点数
 * x    当前解
 * bestx当前的最优解
 * cn   当前顶点数
 * bestn当前最大顶点数
 **/
int a[MAX + 1][MAX + 1] = {
    {0, 0, 0, 0, 0, 0},
    {0, 0, 1, 0, 1, 1},
    {0, 1, 0, 1, 0, 1},
    {0, 0, 1, 0, 0, 1},
    {0, 1, 0, 0, 0, 1},
    {0, 1, 1, 1, 1, 0}
};
int n = MAX;
int x[MAX + 1] = {0};
int bestx[MAX + 1];
int cn;
int bestn;

// i > n 表示找到当前的最优解，将路径保存到bestx数组，将顶点数保存到bestn
// 设置标志变量ok，标识可行性约束函数的结果，ok = 1即表示当前节点可以加入到结果集中
// 对于通过约束函数的结点访问其左子树，并将当前结点添加到路径中，并++结点数
// 再进行上界函数讨论，即访问结点右子树，当右子树中有足够多的结点构成更大的团时，访问右子树
void BackTrack(int i) {
    if (i > n) {
        for (int j = 1; j <= n; j++)
            bestx[j] = x[j];
        bestn = cn;
        return ;
    }
    int ok = 1;
    for (int j = 1; j < i; j++)
        if (x[j] == 1 && a[i][j] == 0) {
            ok = 0;
            break;
        }
    if (ok) {
        x[i] = 1;
        cn++;
        BackTrack(i + 1);
        cn--;
    }
    if (cn + n - i > bestn) {
        x[i] = 0;
        BackTrack(i + 1);
    }
}

void main() {
    BackTrack(1);
    printf("%d\n", bestn);

    for (int i = 1; i <= n; i++)
        printf("%d ", x[i]);
    printf("\n");

    system("pause");
}