25noip 集训

Round 1

light

给出一共 \(2n\) 个数 \(A_i,B_i\)。选取其中一些 \(a\subseteq A,b\subseteq B\)，使得 \(\min(\sum\limits_{i\in a}i,\sum\limits_{j\in b}j)-\vert a\vert-\vert b\vert\) 最大。

\(n\le1\times 10^5\)。

显然，选越大的数约优。于是考虑分别对 \(A,B\) 从大到小排序，设排序后 \(sa_i,sb_i\) 分别表示二者前缀和，答案为 \(\max\limits_{1\le i,j\le n}\min(sa_i,sb_j)-i-j\)。直接做是 \(\mathcal O(n^2)\) 的。

直接分离开，枚举每个 \(i\)，记录比 \(sa_i\) 小的最大的 \(sa_j-j\) 以及最小的使得 \(sb_j>sa_i\) 的 \(j\)，随便什么东西都能维护。

set

给出包含 \(0\sim n-1\) 元素的集合 \(S\)，每个元素的个数为 \(f_i\)。

每次可以删除一个子集 \(T\subseteq S\)（相同元素删除一个），并加入 \(\operatorname{mex}(T)\)。

求最少操作次数使得 \(n\) 在集合内。

\(n\le 50\)。

发现加入 \(i\) 的最优方案就是删除 \(0\sim i-1\)。

倒过来做就做完了。

dist

\(n\) 个人，每个人有位置 \(a_i\)。

\(m\) 次操作，每次加入位置为 \(b_i\) 的人。操作会继承。

人移动速度为 \(1\) 个单位每秒，一段时间所有人都可以自由移动。

对于每次操作，求使得任意两人距离不少于 \(D\) 的最小时间。

\(n\le 2\times 10^5\)。

发现 \(b_i\) 实际上和 \(a_i\) 等价，相当于依次有 \(n+1,n+2,\cdots,n+m\) 个人的最小移动时间。于是只考虑一个数组的情况，把每个人的坐标设为 \(p_i\)，升序。

注意到这个最小移动时间，就是对于任意的 \(i< j\)，都有 \(D(j-i)-(p_j-p_i)\le 2t\)，即 \((p_i-iD)-(p_j-jD)\le2t\)。设 \(f(i)=p_i-iD\)，维护最大的差即可。可以用线段树维护。

注意一点，这个 \(i\) 随着新增元素并不固定。因此考虑维护 \(p_i\) 与 \(D\) 的后缀和，即 \(p_i-(n-i+1)D\)，其中 \(i\) 是当前排名，\(n\) 是当前元素数。那么只需维护最大最小值以及左减右最大差即为答案。

trap

给出大小为 \(n\) 的无根树。一个老鼠从 \(s\) 出发，走过的边会变脏，老鼠不会走脏的边，初始边都是干净的。

每一轮管理员先手，可以选择边堵塞或者打扫一条边（不能打扫堵塞的），或者什么都不做。后手是老鼠走一条边。如果没有干净邻边，老鼠不会走。

管理员的目的是使老鼠走到 \(t\)，且最小化你的操作数（不算不做的轮），老鼠想最大化这个次数。

输出这个次数。

\(n\le 10^6\)。

不妨将 \(t\) 设为根。

考虑 \(s,t\) 相邻的情况。可以发现，在合法的情况下老鼠一定会向下走，否则直接结束。也就是说，老鼠一定尽量往深度更深的地方走。管理员的操作，一定是使老鼠无法继续往更深的地方走。老鼠只有在没有向下的边时，才会往上走。另外，当老鼠无法移动时，管理员可以任意操作任意次。

于是考虑 dp，设 \(f(u)\) 表示老鼠从 \(u\) 走，回到 \(u\) 且只能向上走，对于管理员的最优操作数。根据前文的论述，所有通向子节点的边一定无法走。而要回到 \(u\)，其中一条边必然经过两次。故有转移式：

\[f(u)=\operatorname{2th}\max\limits_{v\in son_u} f(v)+\vert son_u\vert \]

那么在相邻条件下，答案就是 \(f(s)\)。

把这个情况拓展到更一般的情况。老鼠必然会走 \(s\to t\) 的这一路径。同样的，老鼠最多只会向下走一条链。但是我们不知道老鼠从哪个点开始向下。注意到答案具有单调性，即若操作 \(k\) 次满足，操作 \(t\ge k\) 次必然满足。考虑二分，\(mid\) 表示操作次数的上界。check 函数实际上就是在 \(s\to t\) 的链上，堵上 \(f(v)>mid\) 的所有子节点。再维护一个 \(cnt\)，表示当前可用次数，只要最终的 \(mid\ge 0\) 就合法。

Round 2

gift

二分一下长度就可以了。

lis

注意到选中间段一定比选前后缀不优，而前后缀的 LIS 是好求的，再用随便一个数据结构维护一下就做完了。

lego

根号分治做法。

\(\mathcal O(n^2)\) 做法

设 \(f(x)\) 为不考虑连通，\(x\) 列的答案。有转移 \(f(x)=f(x-1)+f(x-2)\)。答案为 \(f(n)^m\)。

设 \(g(x)\) 为考虑连通，\(x\) 列的答案。有转移 \(g(x)=f(x)-\sum\limits_{j=1}^{x-1}g(j)f(x-j)\)。

\(\mathcal O(nm^2)\) 做法

设 \(f(i,j)\) 表示第 \(i\) 列有 \(j\) 个凸起的答案。有转移 \(f(i,j)=\sum\limits_{k=1}^{m}f(i-1,k)\times\dbinom{m-k}{j}\)。答案为 \(f(n,0)\)。

rain

要求的是期望，转化一下，实际上就是看一个货架要被选的概率，显然是可以覆盖它水龙头数量之倒数。

手玩几组样例，画图发现，被统计到的货架是形如下图粉色阴影的类型。

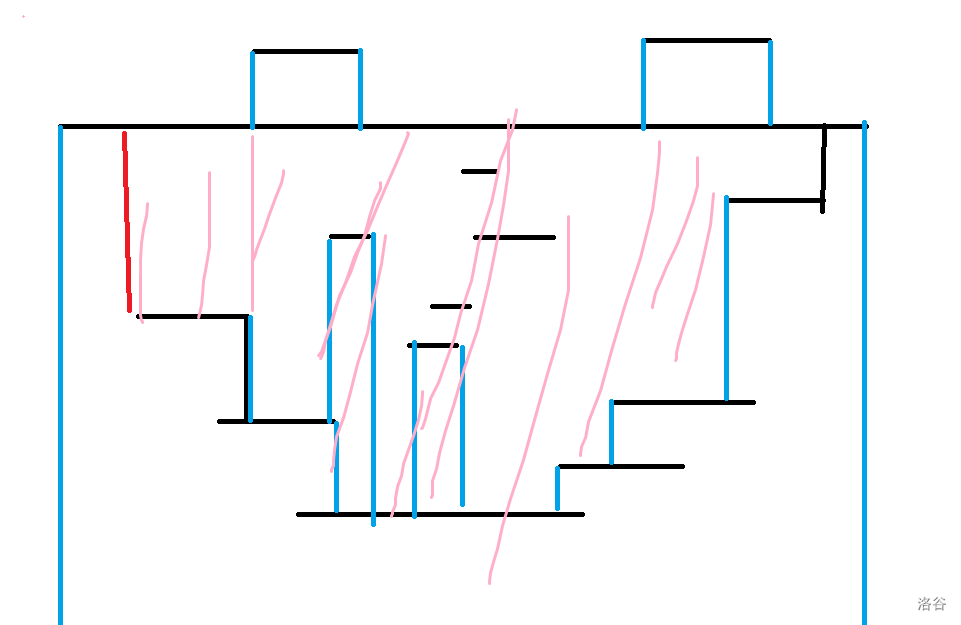
是一个多边形区域，注意到下面的线段覆盖每次都和最低的把其端点覆盖的线段有关，我们称这两种线段为其左右父亲节点。

这个东西满足差分性，于是扫描线一下就做完了？

不是很会写，感觉很麻烦啊我靠。

Round 3

buy

给出 \(n\) 件商品价格 \(p_i\)，你要花费若干轮买完。每轮买的方案如下：

• 买不少于三个，那么最便宜的不要钱。
• 买少于三个，统一 \(q\%\) off。

最小化购买价格。

\(n\le1\times 10^5\)。

显然买少于三个，相当于一个一个买。买三个一定比买多于三个更优，且连续价格比不连续更优。

因此考虑对价格排序，然后设 \(f_i\) 表示买完前 \(i\) 个最小代价。于是 \(f_i=\min(f_{i-1}+(100-q)\times p_{i},f_{i-3}+p_{i-1}+p_i)\)，做完了。

similar

给出长度为 \(n\) 的序列 \(a_i\)，对于他所有长度为 \(l\) 共 \(n-l+1\) 个子段，设第 \(i\) 个子段表示区间 \([i,i+l-1]\)。定义对于任意两个子段 \(x,y\) 距离为对应位置不同字符数量。

\(q\) 次询问，对于每个子段，求其他与其距离不超过 \(k\) 的子段个数。

\(n\le 10000,q\le1000\)。

32 MiB。

可以把询问存下来，总共有 1e7 个，考虑用 short 优化一下，只有 ~19MiB。

然后发现对于两个字段 \([l_1,r_1],[l_2,r_2]\) 拓展到 \([l_1+1,r_1+1],[l_2+1,r_2+1]\) 可以在 \(\mathcal O(1)\) 的时间内完成。于是考虑计算所有子串与 \([1,l]\) 的距离。再反过来做一遍，就统计完了。复杂度 \(\mathcal O(n(n+q))\)。

point

给出平面上 \(n\) 个关键点，求使得左下角和右上角为关键点，且矩形内部不存在其他关键点（不包括边界）的矩形个数。

保证横纵坐标互不相同，\(n\le2\times 10^5\)。

看来平面上关于点对的问题，差不多都能想到有关分治的做法，第一眼感觉和平面最近点对很像。

固定左下角的点 \((x_1,y_1)\)，考虑什么样的点可以与其配对。假设 \((x_2,y_2)\) 与其配对。那么一定不存在点 \((a,b)\) 使得 \(a\in(x_1,x_2),b\in(y_1,y_2)\)。即不存在在这个范围内被 \((x_2,y_2)\) 二维偏序的点，转化一下，如果按照横坐标排序，那么 \(y_2\) 就是横坐标限定在 \(x>x_1\)，纵坐标限制在 \(y>y_1\) 的关于纵坐标的 前缀最小值。

直接枚举复杂度甚至不如 \(\mathcal O(n^2)\)，于是考虑分治。由于没有横纵坐标都可以任选，于是随便取一维，这里就取横坐标。考虑左侧点怎么样才可以与右侧点匹配。

设在左侧点为 \(P\)，右侧可以与 \(P\) 匹配的点为 \(Q\)，中线横坐标为 \(m\)。根据前面的限制，\(Q\) 必然是横坐标从 \(P_x\) 起，所有 \(y>y_P\) 的前缀最小值。然而倘若引入左侧点，难以维护这个前缀最小值。于是考虑转化，这就相当于对于 \(P_x\sim m\) 中的最小的比 \(y_P\) 大的点 \(U\)，使得 \(y_Q\) 为从 \(m\) 起的前缀最小值且 \(y_Q<y_U\)。也就是说，左侧点 \(P\) 要统计纵坐标在 \((y_P,y_U)\) 之间所有为前缀最小值的右侧点。

考虑对纵坐标扫描线，这样我们就能实时维护对纵坐标有限制的前缀最小值。维护一个单调栈。 由于我们是对纵坐标做的扫描线，因此已经天然满足纵坐标递减的性质。假设栈为 \(S\)，新增点为 \((a,b)\)，只要当栈顶 \(S_{top}\) 的横坐标大于 \(a\)，一直弹出。剩下的就是用数据结构维护单点加区间求和，用树状数组维护即可。

复杂度 \(\mathcal O(n\log^2n)\)。

trade

决策单调性+四边形不等式

我不会，所以不补了。

Round 换掉后的 4

原来的 Round 4 大洋里出问题了，遂换成 Round 5 的题。

permutation

设 \(v(i,j)=\vert p_i-p_j\vert\times\vert i-j\vert\text{ for }j>i\)。对于排列 \(p_i\)，求前 \(k\) 小的 \(v(i,j)\) 的和。
\(1\le k<n\le5\times 10^4\)。

考虑在统计范围内的 \(v(i,j)\) 最大为 \(n-1\)，然后根号乱搞就行了。

sequence

对于 \(n\) 个数 \(a_i\)（不给出），给出 \(m\) 个限制。每个限制形如 \(a_{l}\oplus a_{l+1}\oplus\cdots\oplus a_r=x\)。判断是否合法。
\(n,m\le 2\times 10^5,a_i< 2^{60}\)

并查集板子，扩展域一下就做完了。

and

给出长度为 \(n\) 的环 \(a_i\)，划分这个环，使得每个子环内按位与均非 \(0\)。计数。

\(n\le2\times 10^5,a_i\le 2^{60}\)。

不在环上的做法是简单的，设 \(f_i\) 表示以 \(i\) 为子段结尾的方案数，设 \(p\) 为最靠前的使按位与运算非零的位置，可以直接双指针维护。有 \(f_i=\sum\limits_{j=p-1}^{i-1}f_j\)，前缀和优化可以做到 \(\mathcal O(n\log n)\)。

考虑序列上丢失了哪些情况，发现是序列上前缀和后缀成环的情况。枚举前缀，直接做是 \(\mathcal O(n^2\log n)\) 的。

由于与运算的性质，前缀按位与运算的值至多有 \(\mathcal O(\log V)\) 种，即本质不同的情况有 \(\mathcal O(\log V)\) 种。对这些本质不同值分别 dp，复杂度可以做到 \(\mathcal O(n\log V\log n)\)。

osu