动态规划优化 I
线段树优化
我们已经接触过了许多动态规划的类型, 可以使一个问题在多项式复杂度如 \(\mathcal O(n^3)\), \(\mathcal O(n^2)\) 求解. 但是有时 \(n\) 上限会达到 \(10^5\) 甚至 \(10^6\), 此时这种复杂度就显得过于拙劣了. 那么有没有有一种方法能优化复杂度呢?
考虑形如 \(f(i)=\max\limits_{j=1}^{i-1}\{g(f(j))\}+h(i)\) 的转移方程, 若以朴素算法转移, 那么时间复杂度会达到 \(\mathcal O(n^2)\). 但是我们注意到, 这个式子实际上在查询一段区间的最值, 于是自然可以引入数据结构, 线段树是一种处理区间问题的数据结构.
我们只需要定义线段树节点 \(c[l,r]\) 表示区间 \([l,r]\) 的最大 \(g(f(j))\), 即可以 \(\log n\) 的复杂度进行转移. 线段树优化 DP 的思想大致如此.
模板: CF115F Linear Kingdom Races
有 \(n\) 条路可以修, 修第 \(i\) 条路的花费是 \(w_i\). 有 \(k\) 个活动, 第 \(i\) 个活动由三元组 \([l_i,r_i,p_i]\) 表示, 指若修了 \([l_i,r_i]\) 内所有路则有收益 \(p_i\). 求最大收益.
Solution:
设 \(f(i)\) 表示前 \(i\) 条路的最大值. 若第 \(i\) 条不修, 答案为 \(f(i)\). 若修, 则枚举从哪个位置修. 故 \(f(i)=\begin{cases}f(i-1),\\\max\{f(j)+val(j+1,i)-cost(j+1,i)\end{cases}\)
可能会对第二个式子有疑惑, 如果越过 \(j\) 的收益如何统计? 不必担心, 这种情况会导致答案偏小, 然而我们 \(j\) 取遍整个区间, 且取最大值, 故这种情况必定被答案排除在外.
直接 dp 复杂度是 \(\mathcal O(n^2)\).
我们现在 dp 的瓶颈是降低第二个式子的复杂度, 我们考虑线段树优化.
由于比赛以 \(r\) 结尾才有贡献, 故以 \(r\) 偏序, 枚举以 \(r\) 结尾的所有比赛. 我们设线段树节点 \(c[l,r']\) 的意义为 \(\max\limits_{i=l+1}^{r'}\{f(i)+val(i,r)-cost(i,r)\}\). 每次枚举到一个新的 \(r\) 时, 即需要修新路, 故将 \(c[0,r-1]\) 减去 \(w_r\). 即 \(cost(i,r+1)=cost(i,r)+w_r\). 后枚举可以作出贡献的 \(l\), \(c[0,l-1]\) 加上贡献 \(p\), 即包含区间 \([l,r]\) 的所有区间加上 \(p\). 于是, 进行状态转移, \(f(r)=\max\{f(r-1),c[0,r-1]\}\). 最后, \(r\gets r+1\), 令 \(r'=r+1\), 已求出 \(f[r]\), 故将 \(c[r,r']\gets f[r]\)
scanf ("%d%d", &n, &m);
for (int i = 1; i <= n; i ++) scanf ("%lld", w + i);
for (int i = 1; i <= m; i ++) {
ll L, R, P;
scanf ("%lld%lld%lld", &L, &R, &P);
range[R].push_back ({L, P});
}
for (int R = 1; R <= n; R ++) {
add (1, 0, n, 0, R - 1, -w[R]);
for (auto A : range[R]) {
auto L = A.first, P = A.second;
add (1, 0, n, 0, L - 1, P);
}
dp[R] = max (dp[R - 1], query (1, 0, n, 0, R - 1));
modify (1, 0, n, R, R, dp[R]);
}
练习 [NOIP2023] 天天爱打卡
与模板并无区别, 离散化一下即可.
例题 ARC073D Many Moves
长度为 \(n\) 整数轴上的两个点 \(A,B\) 初始处于 \(a,b\), 共 \(Q\) 次操作, 每次操作给出 \(x_i\), 要求将任意一个点移动到 \(x_i\), 移动一个单位长度需要 1s. 求最短时间. \(n,Q\le2\times10^5\).
Solution:
设 \(f(i,j)\) 操作完前 \(i\) 个要求, 表示一个棋子在 \(x_i\), 另一个棋子在 \(j\) 的最短操作时间. 显然有状态转移式:
爆空间, 怎么办?
状态优化.
从状态定义中, 我们发现需要根据操作顺序进行 DP, 故将第一维省去, 空间线性.
直接 DP 是 \(\mathcal O(nQ)\) 的, 怎么办?
线段树优化.
第一个式子无需优化.
第二个式子可以拆成 \(\begin{cases}\min\{f(i-1,j)+j\}-x_{i}, & j\ge x_i, \\ \min\{f(i-1,j)-j\}+x_{i},&j<x_i\end{cases}\)
对于当前枚举到的 \(i\), 我们设 \(c_k[l,r]\) 表示 \(\min\limits_{j=1}^n\{f(i-1,j)-j\times(-1)^{k}\}\), 则上式即可化为
\(\min\{c_0[x_i,n],c_1[1,x_i]\}\). 于是复杂度就变成了 \(\mathcal O(Q\log n)\).
scanf ("%d%d%d%d", &n, &q, &a, &b); SMT :: build (1, 1, n); x[0] = a;
SMT :: modify (1, b, b, 0);
for (int i = 1; i <= q; i ++) {
scanf ("%d", x + i);
ll fir = SMT :: query (1, x[i], n, 1) - x[i]; // query 的第四个元素指哪一个线段树.
ll sec = SMT :: query (1, 1, x[i], 0) + x[i];
SMT :: add (1, 1, n, abs (x[i] - x[i - 1]));
SMT :: modify (1, x[i - 1], x[i - 1], min (fir, sec));
}
printf ("%lld\n", SMT :: query (1, 1, n, 2));
单调队列优化
形如 \(f(i)=\min/\max \{f(j)+A(i)+B(j)\}\) 的式子,其中 \(A(i)\) 是关于 \(i\) 的函数,\(B(j)\) 是关于 \(j\) 的函数。我们将 \(A(i)\) 分离出来,式子变为 \(f(i)=\min/\max \{f(j)+B(j)\}+A(i)\),对 \(f(j)+B(j)\) 进行单调维护,即可将原 \(\mathcal O(n^2)\) 的复杂度降到 \(\mathcal O(n)\)。
P1886 滑动窗口 /【模板】单调队列
给出一段 \(n\) 的序列,求每个长度为 \(k\) 的子段中元素的最大值。\(n\le 10^6\)。
以元素大小为第一关键字,构成单调队列。每次的队头即为答案。
代码以前写的太丑陋了,看下面例题的吧。
P3572 [POI 2014] PTA-Little Bird
\(n\) 棵树,第 \(i\) 树树高为 \(d_i\)。从第 \(1\) 棵开始,每次可以从第 \(i\) 棵飞到第 \(j\in[i+1,i+k]\) 棵。若 \(d_j\ge d_i\),则劳累值加 \(1\)。求飞到第 \(n\) 棵树的最小劳累值。\(n\le 10^6\)。
设 \(f(i)\) 表示飞到第 \(i\) 棵的最小劳累值,则 \(f(i)=\min\limits_{j\in[i-k,i)}\{f(j)+[d_j\ge d_i]\}\)。时间复杂度 \(\mathcal O(n^2)\),爆了。
注意到每次增加值至多为 \(1\),那么可以想到用单调队列维护。比较第一关键字是 \(f(i)\) 大小,第二关键字是 \(d_i\) 大小。每次 dp 直接选队头元素进行比较即可。
memset (f, 0x3f, sizeof f);
f[1] = 0; int l = 1, r = 0;
q[++ r] = 1;
for (int i = 2; i <= n; i ++) {
while (l <= r && i - q[l] > k) l ++;
f[i] = f[ q[l] ] + (d[i] >= d[ q[l] ]);
while (l <= r && (f[i] < f[ q[r] ] || f[ q[r] ] == f[i] && d[i] >= d[ q[r] ])) r --;
q[++ r] = i;
}
printf ("%d\n", f[n]);
斜率优化
对于形如 \(F(i)=\min/\max\{F(j)+A(i)+B(j)+A(i)B(j)\}\) 且满足 \(A(i)\) 单调增的状态转移式,可以进行 斜率优化 来降低复杂度。通过下面这道 经典例题 来入门。
P3195 [HNOI2008] 玩具装箱
设 \(S_i=\sum\limits_{j=1}^iC_i\),\(F(i)\) 表示答案。\(F(i)=\min\{F(j)+(S_i+i-S_j-j-L-1)^2\}\),设 \(A(i)=S_i+i\),\(B(j)=S_j+j+L+1\)。
\(\begin{aligned}F(i)&=F(j)+(A(i)-B(i))^2 \\ &=F(j)+A(i)^2+B(j)^2-2A(i)B(j) \\ &=F(j)+B(j)^2-2A(i)B(j)+A(i)^2 \end{aligned}\)
即 \(F(j)+B(j)^2=2A(i)B(j)+F(i)-A(i)^2\)。
我们令 \(Y(j)=F(j)+B(j)^2\),\(k=2A(i)\),\(X(j)=B(j)\),\(b=F(i)-A(i)^2\)。
则上式即为 \(Y(j)=k\cdot X(j)+b\),呈直线的点斜式。
对于所有的 \(j\),构成多个点 \((B(j),F(j)+B(j)^2)\)。
由于 \(A(i)^2\) 是定值,\(b=F(i)-A(i)^2\)。故截距 \(b\) 越小,\(F(i)\) 就越小。
我们只需找到依次过所有点的直线中,截距最小的,即可求得 \(F(i)\)。
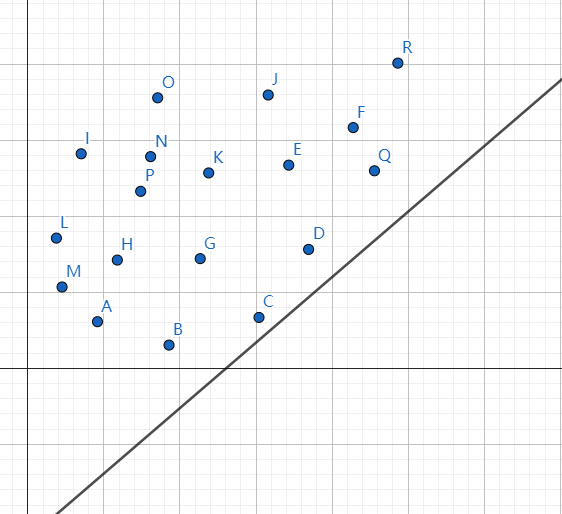
我们以这张图为例,这条直线的斜率介于 \(BC\) 和 \(CD\) 之间,那么我们向上平移这条直线,显然最先触碰到 \(C\) 点。那么 \(C\) 点就是这条直线的最优解。
也就是说,我们取 \(C\) 点的 \(j\) 值,这个 \(j\) 就是这个斜率为 \(k=2A(i)\) 直线即 \(F(i)\) 的最优策略。直接转移即可得到 \(F(i)\)。
这条直线可以介于许多对线段斜率之间,然而为了使截距最小,我们选择的点必须在这所有点的外围,也就是这些点的 凸包 上。由于直线的斜率 \(k=2A(i)\) 是单调增的,因此可以考虑使用 单调队列 维护所有点,这也与上一个优化方式不谋而合。
问题也便转化为了如何动态维护凸包。不妨假设已经维护了 \(k\) 个点的凸包,那么如何处理新增点?
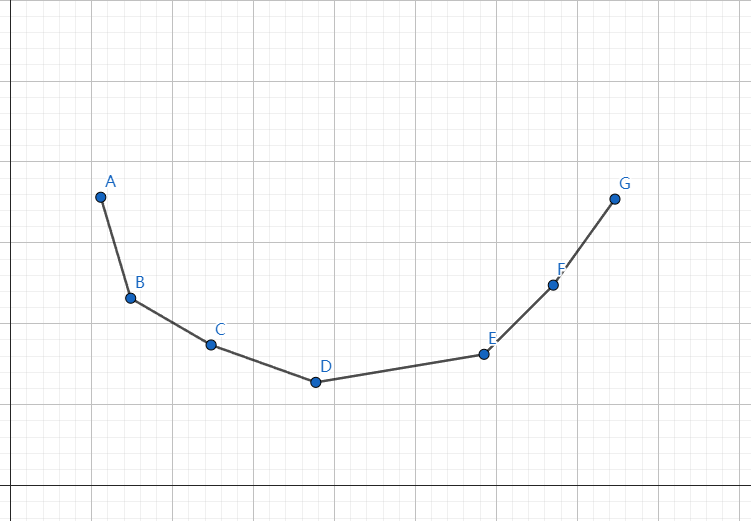
我们很容易发现凸包上相邻两点连线的斜率是不断递增的,于是可以做出以下分类讨论:
假设新增点为 \(P\)。
- 如若 \(k_{PG}\ge k_{FG}\),那么直接入队即可。
- 如若 \(k_{PG}<k_{FG}\),那么需要一直从队尾出队,直至 \(P\) 与队尾点的斜率不小于上一个点与队尾点的斜率。
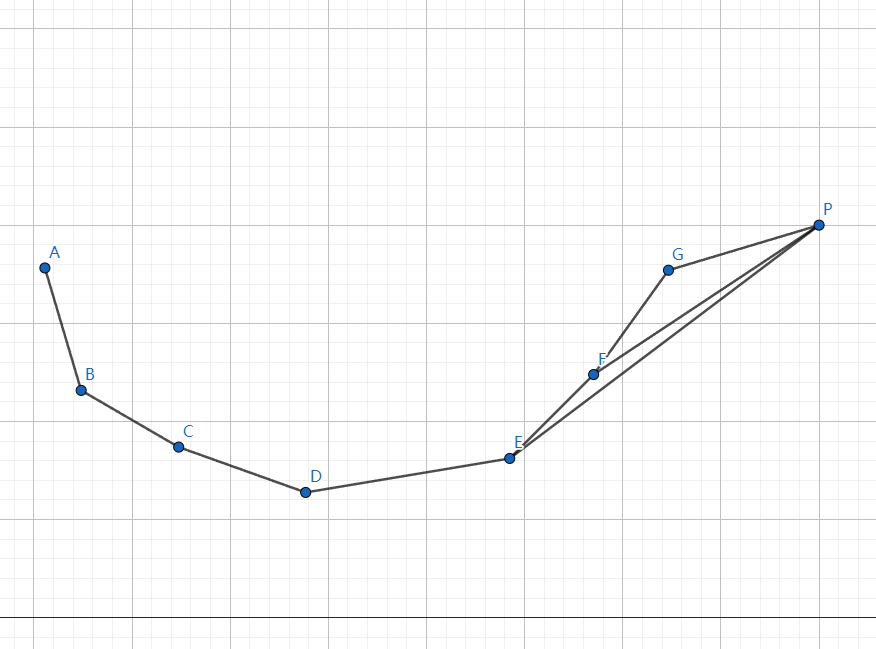
那么如若新增的 \(P\) 点在 \(G\) 点左侧,怎么办?
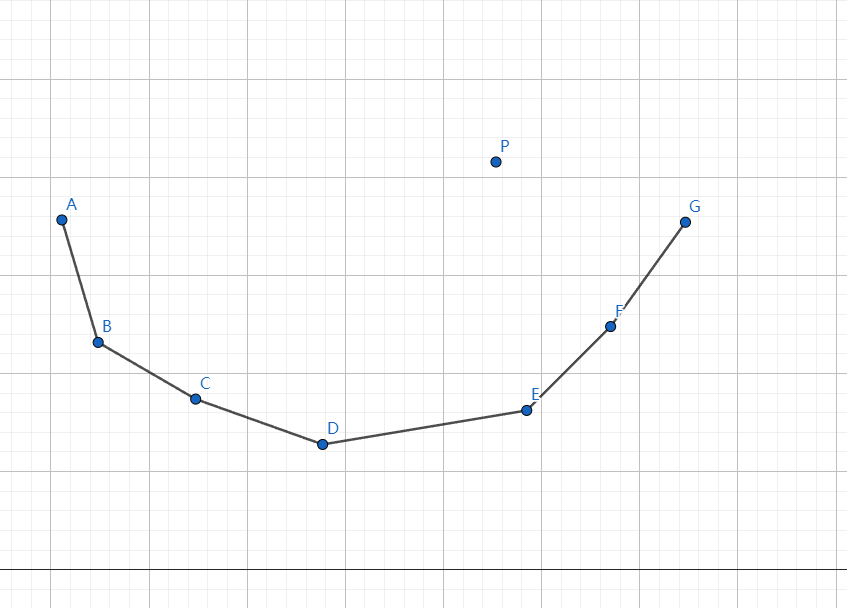
很简单,不入队即可。而且由于本题的 \(X(j)=S_j+L+1+j\),即每个点的横坐标是递增的,因此无需考虑这种情况。
其实到这里已经可以发现,我们实际上维护的是并非完整的凸包,而是凸包的 下凸壳,这是因为我们需要求得截距的 最小值,并非每道斜率优化的题目都必须维护下凸壳,例如求截距最大值便是维护上凸壳。
如此,我们基本上已经了解了斜率优化的所有步骤,总结一下如下:
- 从队头开始,若队头与其相邻点连成线段的斜率小于 \(k=2A(i)\),出队;
- 那么队头就为所说的最优解,取队头点进行状态转移;
- 删除队尾点直至使相邻斜率单调增,后加入当前点 \((X(i),Y(i))\)。
值得注意的是,至少有两个点才能进行斜率计算,如若没有两个点,那么无需操作。
#include <cmath>
#include <iostream>
#define ll long long
using namespace std;
const int MAXN = 5e4 + 10;
int n, l;
ll s[MAXN], A[MAXN], B[MAXN], dp[MAXN], q[MAXN];
ll sq (ll x) { return x * x; }
ll X (int i) { return B[i]; }
ll Y (int i) { return dp[i] + sq (B[i]); }
double slope (int i, int j) { return (double)(Y (i) - Y (j)) / (X(i) - X(j)); }
int main (void) {
scanf ("%d%d", &n, &l); l ++;
for (int i = 1; i <= n; i ++) scanf ("%lld", s + i), s[i] += s[i - 1], A[i] = s[i] + i, B[i] = s[i] + i + l;
B[0] = l;
int l = 1, r = 0; q[++ r] = 0;
for (int i = 1; i <= n; i ++) {
while (l < r && slope (q[l], q[l + 1]) < 2 * A[i] ) ++ l;
dp[i] = dp[ q[l] ] + sq ((A[i] - B[ q[l] ]));
while (l < r && slope (i, q[r]) < slope (q[r - 1], q[r])) -- r;
q[++ r] = i;
}
printf ("%lld\n", dp[n]);
return 0;
}
- 为什么要先入队一个 \(0\)?
- 如若不入队,则第一个点必不会被删除,违反了上述原则。
P2120 [ZJOI2007] 仓库建设
有 \(n\) 个仓库,第 \(i\) 个仓库有 \(p_i\) 个物品,修建防护的代价为 \(c_i\),距离仓库 \(1\) 的距离为 \(x_i\)。每个仓库都可修建防护,且每个物品必须在防护之下。如若 \(j\) 仓库不修,那么需要花费 \(p_j\times p_k\) 的代价转移到修建防护的 \(k\) 仓库(\(k>j\))。\(n\le 10^6\),求最小代价。
先想到了直接设计状态 \(f(i)\):前 \(i\) 个仓库的所有物品都处于防护之下的最小代价。然后翻转一下 \(x_i,c_i,p_i\),转移式看起来很好写:\(f(i)=\min\limits_{j\in[1,i)}\{f(j-1)+c_j+\sum\limits_{k=j}^i(x_j-x_k)\cdot p_k\}\),然后发现这个式子中涉及了两个量,我做斜率优化时没有成功,这种方法只能有 \(\mathcal O(n^2)\) 做法。
于是换个思路,反着 dp。设 \(f(i)\):最后一个仓库建在 \(f(i)\) 的最优解。转移式也是比较显然的:\(f(i)=\min\limits_{j\in[0,i)}\{f(j)+c_i+\sum\limits_{k\in[j+1,i]}(x_i-x_k)\cdot p_k\}\)
然后令 \(A(i)=\sum\limits_{k\in[1,i]}x_ip_i\),\(B(i)=\sum\limits_{k\in[1,i]}p_i\),那么就是 \(f(i)=\min\limits_{j\in[0,i)}\{f(j)+c_i+x_i\cdot(B(i)-B(j))-A(i)+A(j)\}\)。
整理一下,于是 \(f(j)+A(j)=x_i\cdot B(j)+(A(i)+f(i)-x_i\cdot B(i)-c_i)\)。
维护方法与上题同理。
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;
const int MAXN = 1e6 + 10;
int n;
ll x[MAXN], p[MAXN], c[MAXN];
ll A[MAXN], B[MAXN], f[MAXN];
int q[MAXN], l = 1, r = 1;
ll X (int i) { return B[i]; }
ll Y (int i) { return f[i] + A[i]; }
double slope (int i, int j) { ll dY = Y (j) - Y (i); return B[i] == B[j] ? (dY > 0 ? 1e18 : (dY < 0 ? -1e19 : 0)) : (double)dY / (double)(X (j) - X (i)); }
int main (void) {
scanf ("%d", &n);
for (int i = 1; i <= n; i ++) {scanf ("%lld%lld%lld", x + i, p + i, c + i);}
for (int i = 1; i <= n; i ++) A[i] = A[i - 1] + x[i] * p[i], B[i] = B[i - 1] + p[i];
for (int i = 1; i <= n; i ++) {
while (l < r && slope (q[l], q[l + 1]) < x[i]) ++ l; int j = q[l];
f[i] = f[j] + c[i] - ( A[i] - A[j] - x[i] * (B[i] - B[j]) );
while (l < r && slope (q[r], i) < slope (q[r - 1], q[r])) r --;
q[++ r] = i;
}
ll ans = f[n];
int i = n; while (i && !(B[i] - B[i - 1])) i --, ans = min (ans, f[i]);
printf ("%lld\n", ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号