代码随想录算法训练营Day17 二叉树part03|110.平衡二叉树、257.二叉树所有路径、404.左叶子之和

今日内容

1. 110.平衡二叉树
2. 257.二叉树所有路径
3. 404.左叶子之和 

110.平衡二叉树 （优先掌握递归）

平衡二叉树：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1

二叉树节点的高度：距离叶子节点的高度

二叉树节点的深度：距离根节点的深度（指从根节点到该节点的最长简单路径边的条数）

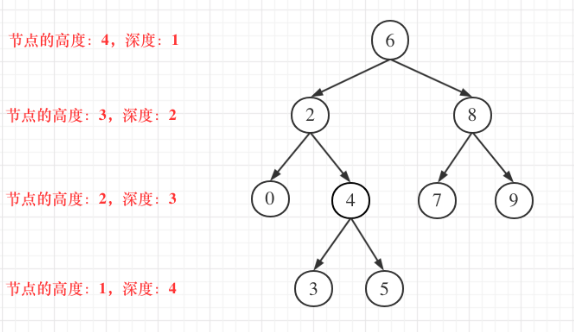
求高度：后序遍历（左右中）

求深度：前序遍历（中左右）

后序：

　　根据左右子树的情况返回给父节点，一层层向上

前序：

　　一直向下遍历，往下统计

做题思路

1. 求高度

递归三部曲：

① 第一步：确定递归函数的参数和返回值

　　　　参数：传入当前节点

　　　　返回值：以当前传入节点为根节点的树的高度，如果不是平衡二叉树，则返回 -1

　　　　const TreeHigh = function(node){}

　　　　let leftHeight = TreeHigh(node.left)

　　　　let rightHeight = TreeHigh(node.right)

　　　　if(leftHeight === -1 || rightHeight === -1) return -1

② 第二步：确定终止条件

　　　　遇到空姐点则终止，返回0，表示当前节点为根节点的树高度为0

　　　　if(node === null) return 0

③ 第三步：明确单层递归的逻辑　　　　

　　　　let leftHeight = TreeHigh(node.left)

　　　　let rightHeight = TreeHigh(node.right)

　　　　let result = 0;

　　　　if(abs(leftHeight,righeHeiht) >1 ) return -1;

　　　　else{

　　　　　　result = 1+max(leftHeight,rightHeight);// 父节点的高度，等于左右子树中高度最大值+1（1为本身高度）

　　　　}

　　　　return result;

左右子树的高度差>1，则向上返回-1

/*
 * @lc app=leetcode.cn id=110 lang=javascript
 *
 * [110] 平衡二叉树
 */

// @lc code=start
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isBalanced = function(root) {
    // 1. 确定参数和返回值
    const TreeHigh = function(node) {
        // 2.确定终止条件
        if (node === null) return 0;
        // 3. 确定单层递归逻辑
        let leftHeigh = TreeHigh(node.left);
        let rightHeigh = TreeHigh(node.right);
        // 如果leftHeigh 和 rightHeigh 中有-1，则返回-1
        if (leftHeigh === -1 || rightHeigh === -1) return -1;
        // 如果左右子树高度差>1，返回-1
        if (Math.abs(leftHeigh - rightHeigh) > 1) return -1;
        // 正常情况：

        return 1 + Math.max(leftHeigh, rightHeigh);
    }
    return !(TreeHigh(root) === -1);
};

 

 257. 二叉树的所有路径 （优先掌握递归）  

回溯

不是太懂这段代码

/*
 * @lc app=leetcode.cn id=257 lang=javascript
 *
 * [257] 二叉树的所有路径
 */

// @lc code=start
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {string[]}
 */
var binaryTreePaths = function(root) {
    // 递归遍历+递归三部曲
    let res = [];
    // 1. 确定递归函数，函数参数
    const getPath = function(node, curPath) {
        //2. 确定终止条件，到叶子节点就终止
        if (!node.left && !node.right) {
            curPath += node.val;
            res.push(curPath);
            return;
        }
        // 3.确定单层递归逻辑
        curPath += node.val + '->';
        node.left && getPath(node.left, curPath);
        node.right && getPath(node.right, curPath);
    }
    getPath(root, '')
    return res;
};

404.左叶子之和 （优先掌握递归）

注意：节点A的左孩子不为空，且左孩子的左右孩子都为空（说明是叶子节点），那么A节点的左孩子为左叶子节点

 if (node.left !== null && node.left.left == NULL && node.left.right == null) { // 左叶子节点处理逻辑  } 

不是严格意义上的递归写法，定义了遍历result，直接在遍历到左叶子时进行相加

/*
 * @lc app=leetcode.cn id=404 lang=javascript
 *
 * [404] 左叶子之和
 */

// @lc code=start
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var sumOfLeftLeaves = function(root) {
    //1. 确定函数参数,与返回值
    let result = 0;
    if (root == null) return 0;
    const sumLeftLeave = function(node) {
        //2. 确定终止条件
        if (node == null) return;

        //3. 单层递归逻辑
        if (node.left !== null && !node.left.right && !node.left.left) {
            result += node.left.val;
        }
        node.left && sumLeftLeave(node.left);
        node.right && sumLeftLeave(node.right);
    }
    sumLeftLeave(root);
    return result;
};

严格一点的写法（参考答案）

var sumOfLeftLeaves = function(root) {
    //采用后序遍历 递归遍历
    // 1. 确定递归函数参数
    const nodesSum = function(node) {
        // 2. 确定终止条件
        if(node === null) {
            return 0;
        }
        let leftValue = nodesSum(node.left);
        let rightValue = nodesSum(node.right);
        // 3. 单层递归逻辑
        let midValue = 0;
        if(node.left && node.left.left === null && node.left.right === null) {
            midValue = node.left.val;
        }
        let sum = midValue + leftValue + rightValue;
        return sum;
    }
    return nodesSum(root);
};

 

 

收获

1. 平衡二叉树中，高度与深度的定义

2. 递归与回溯（回溯还有点不是太明白）