【机器学习】最小二乘法的解析解——问题总结

【机器学习】最小二乘法的解析解——问题总结

今天开始学习最小二乘法，读老师的slides时，遇到了一些问题：

• 各个矩阵的大小？

• 关于运算结果的求导（矩阵求导）？

• 如何计算 \(\hat{\beta_0}\) 的大小？

下面是老师的slides：

矩阵大小

关于 \(\boldsymbol{X}\)

\(\boldsymbol{X}\) 是指输入变量的矩阵，叫做特征矩阵。
对于每一组数据，有 \(p\) 个变量，那么可以记为 \(X_i=[x_1,x_2,\cdots,x_p]^T\)
有 \(n\) 组数据，那么就可以将这些变量组成一个 $p\times $n 大小的矩阵。

实际上，因为 \(n\) 是数据量，一般会远大于变量数 \(p\) ，在应用时，会使用 \(\boldsymbol{X}^T\) （据说这样可以进行CPU的多核并行计算，具体为啥不懂）。

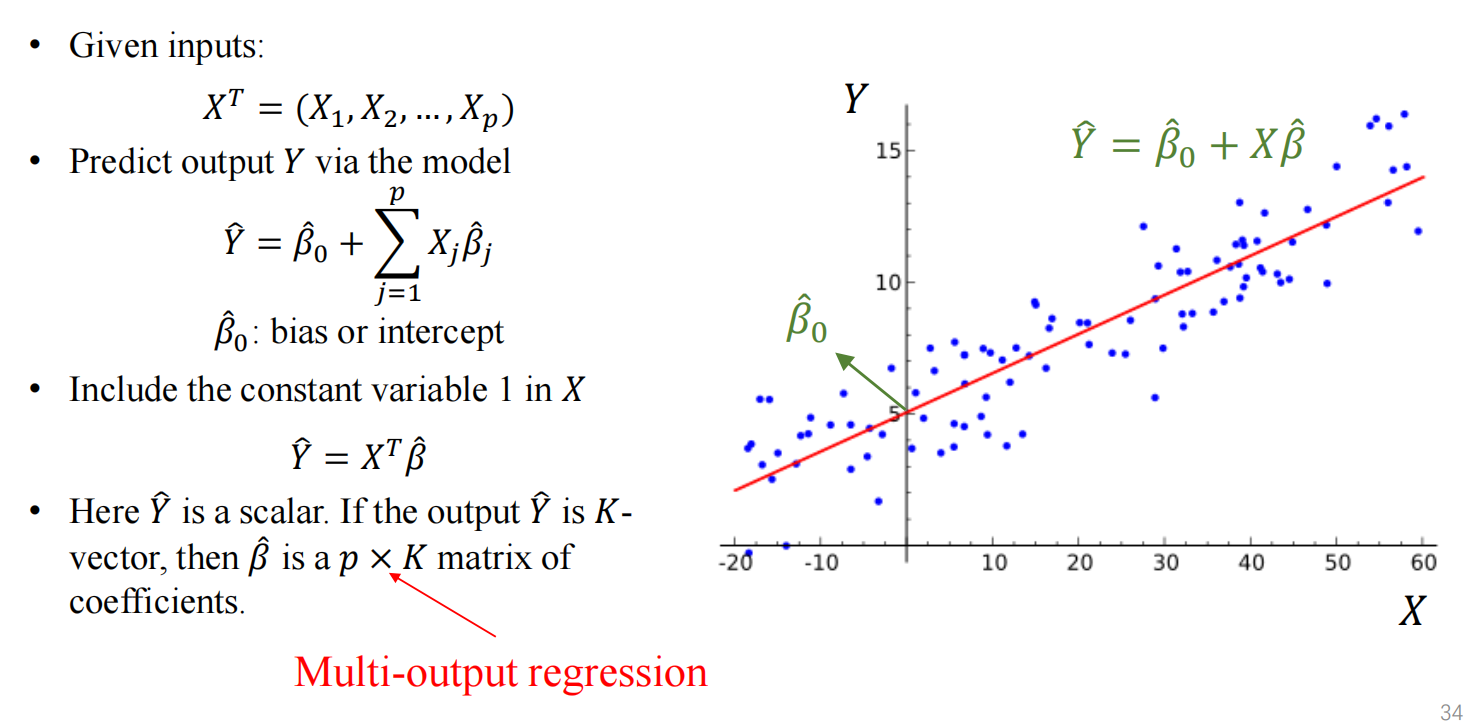
关于 \(\boldsymbol{\hat{Y}}\) 和 \(\boldsymbol{Y}\) ，以及 \(\beta\)

首先这二者一定相等，因为一个是预测值，一个是实际值，那么考虑两种情况：

• 当每一组结果的输出都只有一个标量 \(y_i\) 时， \(\boldsymbol{\hat{Y}}\) 和 \(\boldsymbol{Y}\) 就是向量，即 \(\boldsymbol{Y}=[y_1,y_2,\cdots,y_n]^T\) ，此时的 \(\beta\) 也是一个向量，通过矩阵乘法，得到 \(\hat{y_i}=X_i \beta=[x_1\beta_1,x_2\beta_2,\cdots,x_p\beta_p]\) 。
• 当每一组结果的输出是一组向量 \(Y_i=[y_1,y_2,\cdots,y_k]\) 时，\(\boldsymbol{\hat{Y}}\) 和 \(\boldsymbol{Y}\) 是 \(n\times k\) 的矩阵，此时的 \(\beta\) 就是一个 \(p\times k\) 的矩阵了。

矩阵求导

这个话题在线性代数课程中很少涉及，主要原因应该是当时还没有学多元函数的求导，但是在最小二乘法求最佳的 \(\beta\) 向量时是避不开的。

关于向量的求导

高数和线代的衔接点：
考虑对 \(f(X)\) 关于 \(X\) 求导，其中 \(X=[x_1,x_2,\cdots,x_n]^T\)，
实际上就是多元函数 \(f(x_1,x_2,\cdots,x_n)\) 关于它的每一个自变量 \(x_1,x_2,\cdots,x_n\) 求导，
即 \(\frac{df}{dX}=[\frac{df}{d{x_1}},\frac{df}{dx_2},\cdots,\frac{df}{dx_n}]\)

一些重要的点：

• \(X\) 和 \(X^T\) 关于 \(X\) 求导的结果都是 \(I\) （单位矩阵）；
• 遵循链式求导法则，以及前导后不导等等；

P.S. 关于矩阵的求导，实际上目前还没有用到，但是稍微学了一下，在此记录一下参考资料，主要是这篇 ，anyway 似乎不管矩阵怎么作为一个变量来求导，最后求出的结果 \(\hat{\beta}\) 也一样是 \((\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T \boldsymbol{y}\)

求解系数向量 \(\beta\)

这里根据上面的运算规则，推导一遍 \(\beta\) 的解析解是怎么来的（这里先假设每组数据的输出结果 \(y\) 是一个标量：

之前我们已经计算出了预测值的向量 \(\boldsymbol{\hat{y}}=[X_1^T\beta,X_2^T\beta,\cdots,X_p^T\beta]\) ，以此计算出损失函数

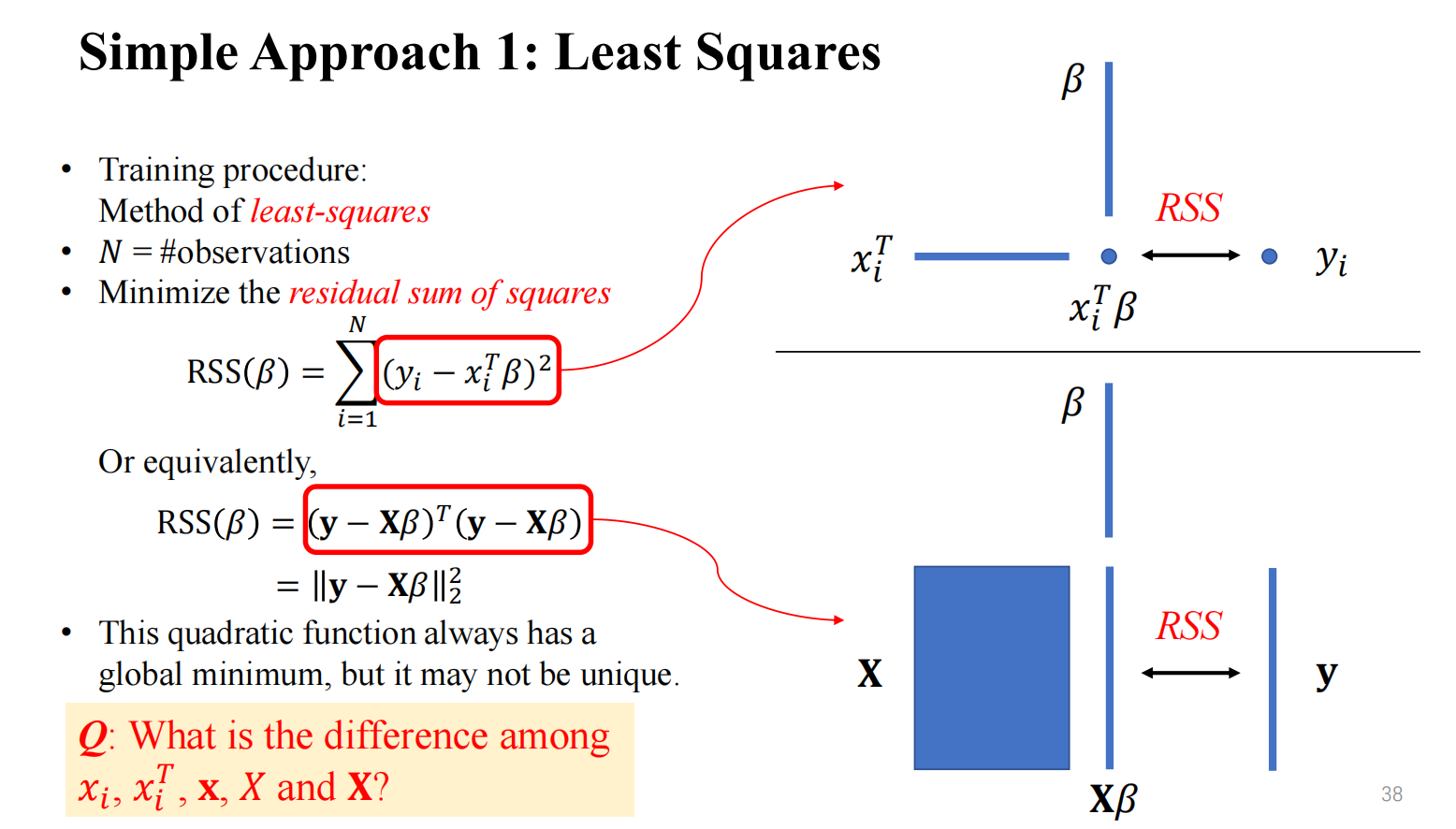
\(RSS(\beta)=\Sigma_{i=1}^{N}(y_i-X_i^T\beta)^2\) （这里平方是为了防止差值的负数与正数抵消）

写成矩阵形式，为 \(RSS(\beta)=(\boldsymbol{y}-\boldsymbol{X}\beta)^T(\boldsymbol{y}-\boldsymbol{X}\beta)\)

\(RSS(\beta)\) 是一个关于向量 \(\beta\) 的函数，并且可以观察出其为一个关于 \(\beta\) 的二次函数。

现在要求出 \(RSS(\beta)\) 最小的自变量 \(\beta\) ，那么只需要对 \(RSS(\beta)\) 求导，导数为 \(0\) 的地方就是要求的最佳系数向量 \(\hat{\beta}\)

\[\begin{align} \frac{dRSS}{d\beta}&=-\boldsymbol{X}^T(\boldsymbol{y}-\boldsymbol{X}\beta)-\boldsymbol{X}(\boldsymbol{y}-\boldsymbol{X}\beta)^T\\ &=-\boldsymbol{X}^T\boldsymbol{y}+\boldsymbol{X}^T\boldsymbol{X}\beta-\boldsymbol{X}\boldsymbol{y}^T+\boldsymbol{X}\boldsymbol{X}^T\beta^T\\ &=-2\boldsymbol{X}^T(\boldsymbol{y}-\boldsymbol{X}\beta)\\ &=0 \end{align} \]

当 \(\boldsymbol{X}^T\boldsymbol{X}\) 是非奇异矩阵时，\(\hat{\beta}=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T \boldsymbol{y}\)

计算 \(\hat{\beta_0}\)

这里 \(\hat{\beta_0}\) 指的是bias/intercept，其实还是挺好计算的，只需要对于每一组数据 \(X_i=[x_1,x_2,\cdots,x_n]^T\) 增加一个维度，变为 \(X_i=[1,x_1,x_2,\cdots,x_n]^T\) 就可以了。