NOIP 2010 题解

机器翻译

单向链表，如果 \(i\) 在内存里，那么用 \(nxt[i]\) 来记录他的下一个单词，每次要插入的时候，如果当前链表的长度小于 \(m\)，那么直接把他插入的末尾，如果等于 \(m\)，就把链表的第一个从链表里弹出来，再把这个元素加进去。

\(Code :\)

#include <bits/stdc++.h>
using namespace std;
int n, m, last = -1, now = -1, siz, nxt[1005], ans;
bool in[1005];
int main()
{
	scanf("%d%d", &m, &n);
	for (int i = 1; i <= n; i ++)
	{
		int x;
		scanf("%d", &x);
		if (!in[x])
		{
			if (siz < m)
			{
				if (now == -1) last = x;
				in[x] = true;
				siz ++;
				if (now != -1) nxt[now] = x;
				now = x;
			}
			else
			{
				in[last] = false;
				last = nxt[last];
				in[x] = true;
				nxt[now] = x;
				now = x;
			}
			ans ++;
		}
	}
	printf("%d", ans);
	return 0;
}

乌龟棋

发现每张卡片的数量很少，于是设 \(dp[a][b][c][d]\) 表示用 \(a\) 张 \(1\)，\(b\) 张 \(2\)，\(c\) 张 \(3\)，\(d\) 张 \(4\)，所能获得的分数的最大值。

转移时考虑一下四种情况：

1. 现在这一步使用的是卡片1，则 \(dp[a][b][c][d] = max(dp[a][b][c][d], dp[a - 1][b][c][d] + a[x])\)。
2. 现在这一步使用的是卡片2，则 \(dp[a][b][c][d] = max(dp[a][b][c][d], dp[a][b - 1][c][d] + a[x])\)。
3. 现在这一步使用的是卡片3，则 \(dp[a][b][c][d] = max(dp[a][b][c][d], dp[a][b][c - 1][d] + a[x])\)。
4. 现在这一步使用的是卡片4，则 \(dp[a][b][c][d] = max(dp[a][b][c][d], dp[a][b][c][d - 1] + a[x])\)。

其中 \(x\) 表示现在到达的格子的编号，即 \(a + 2b + 3c + 4d + 1\)。
枚举 \(a,b,c,d\)，最后答案为 \(dp[\)卡片\(1\)的个数\(][\)卡片\(2\)的个数\(][\)卡片\(3\)的个数\(][\)卡片\(4\)的个数\(]\)。

\(Code :\)

#include <bits/stdc++.h>
using namespace std;
int dp[41][41][41][41], n, m, a[351], cnt[5];
int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
	for (int i = 1; i <= m; i ++)
	{
		int x;
		scanf("%d", &x);
		cnt[x] ++;
	}
	dp[0][0][0][0] = a[1];
	for (int i = 0; i <= cnt[1]; i ++) for (int j = 0; j <= cnt[2]; j ++) for (int u = 0; u <= cnt[3]; u ++) for (int v = 0; v <= cnt[4]; v ++)
				{
					int x = i + j * 2 + u * 3 + v * 4 + 1;
					if (i) dp[i][j][u][v] = max(dp[i][j][u][v], dp[i - 1][j][u][v] + a[x]);
					if (j) dp[i][j][u][v] = max(dp[i][j][u][v], dp[i][j - 1][u][v] + a[x]);
					if (u) dp[i][j][u][v] = max(dp[i][j][u][v], dp[i][j][u - 1][v] + a[x]);
					if (v) dp[i][j][u][v] = max(dp[i][j][u][v], dp[i][j][u][v - 1] + a[x]);
				}
	printf("%d", dp[cnt[1]][cnt[2]][cnt[3]][cnt[4]]);
}

关押罪犯

并查集。

由于只需要知道最大仇恨值的最小值，所以我们先将仇恨按仇恨值从大到小排序。

按照顺序处理每一条边，设当前处理到的两个罪犯是 \(a\) 和 \(b\)。

如果当前的他们不在同一个并查集当中，那么按照敌人的敌人是朋友的原则，我们把 \(a\) 与和 \(b\) 仇恨值最大的哪个罪犯合并在一起，这样就不会让 \(b\) 和和 \(b\) 仇恨值最大的罪犯打起来，同理，将 \(b\) 与和 \(a\) 矛盾值最大的罪犯和并起来。

如果当前两个罪犯已经在一个并查集当中了，那么无论如何也避免不了他们之间的仇恨了，之间输出矛盾值即可。

\(Code :\)

#include <bits/stdc++.h>
using namespace std;
int n, m, fa[20001], x, y, maxn[20001];
struct node
{
    int a, b, c;
} e[100001];
bool cmp(node a, node b)
{
    if (a.c > b.c) return true;
    else return 0;
}
int find(int x) {return fa[x] == x ? x : fa[x] = find(fa[x]);}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i ++) scanf("%d%d%d", &e[i].a, &e[i].b, &e[i].c);
    for (int i = 1; i <= n; i ++) fa[i] = i;
    sort(e + 1, e + m + 1, cmp);
    for (int i = 1; i <= m; i ++)
    {
        x = find(e[i].a);
        y = find(e[i].b);
        int a = e[i].a, b = e[i].b;
        if (x == y)
        {
            printf("%d", e[i].c);
            return 0;
        }
        if (!maxn[a]) maxn[a] = b;
        else fa[find(maxn[a])] = y;
        if (!maxn[b]) maxn[b] = a;
        else fa[find(maxn[b])] = x;
    }
    printf("0");
    return 0;
}

引水入城

猜想：对于任何点，水往下流，其覆盖的必然是一个连续的区间。

证明：反证法。

前提：所有干旱区都能被覆盖到。

假设有一条水流如下图。

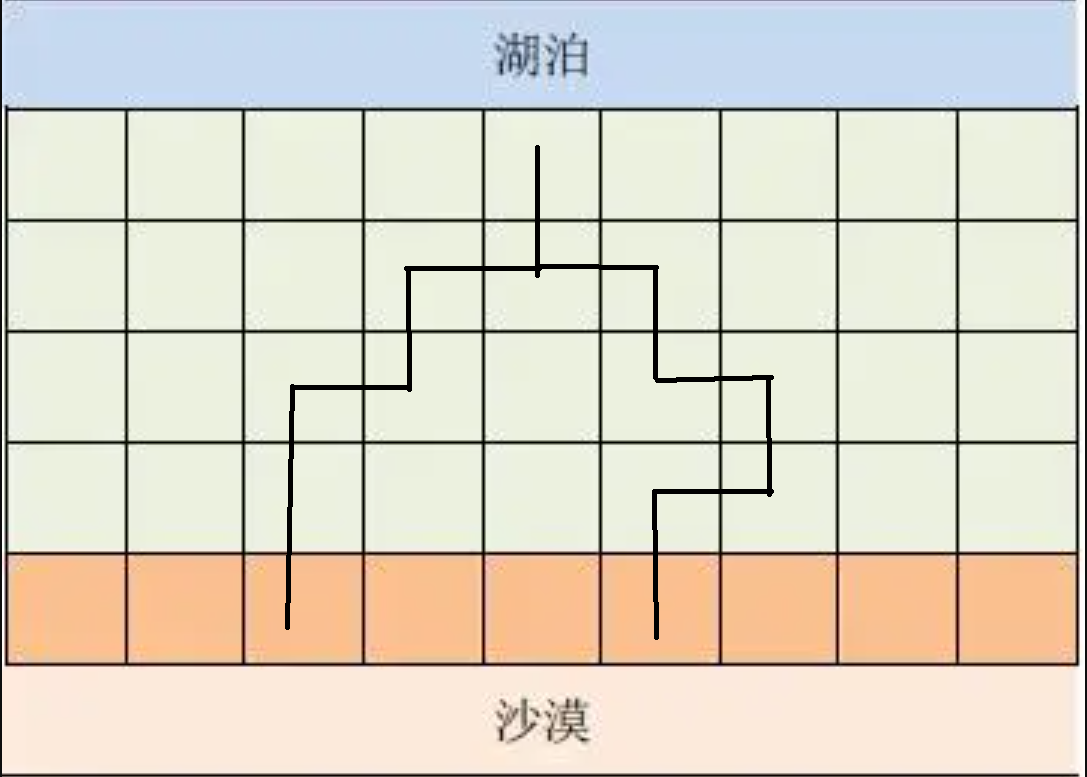
假设这条水流只能覆盖到第 \(n\) 行的第三个和第六个格子，那么如果有其它的格子能够到达第四个和第五个格子，则必定要经过黑色的线，则经过的那个点可以到达中间的第四个格子和第五个格子，与假设矛盾。

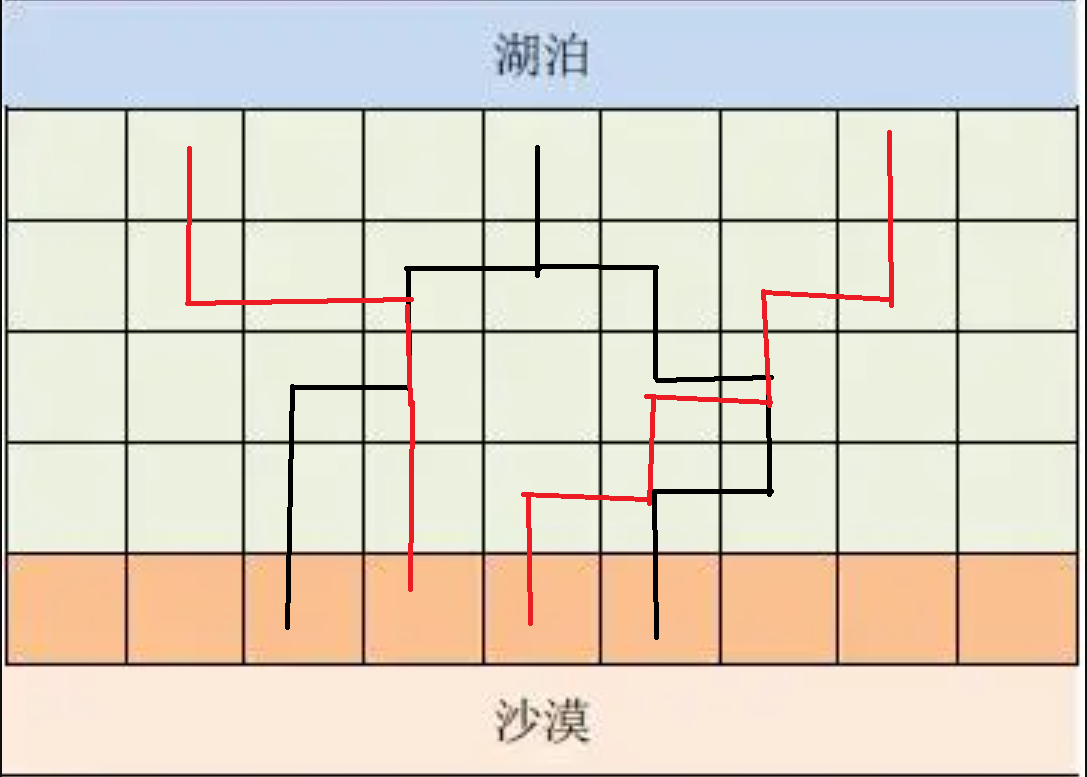
如图，无论是上图那一条红线，都必定经过黑线。

知道了这个，下面我们就只要在dfs的时候把区间的左右端点求出来，再做线段覆盖就行了。

#include <bits/stdc++.h>
using namespace std;
int n, m, a[505][505], l[505][505], r[505][505], dx[] = {1, -1, 0, 0}, dy[] = {0, 0, 1, -1}, cnt;
bool vis[505][505];
void dfs(int x, int y)
{
	vis[x][y] = true;
	for (int i = 0; i <= 3; i ++)
	{
		int fx = x + dx[i], fy = y + dy[i];
		if (fx && fy && fx <= n && fy <= m && a[x][y] > a[fx][fy])
		{
			if (!vis[fx][fy]) dfs(fx, fy);
			l[x][y] = min(l[x][y], l[fx][fy]);
			r[x][y] = max(r[x][y], r[fx][fy]);
		}
	}
}
int main()
{
	scanf("%d%d", &n, &m);
	memset(l, 0x7f, sizeof(l));
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= m; j ++) scanf("%d", &a[i][j]);
	for (int i = 1; i <= m; i ++)
		l[n][i] = r[n][i] = i;
	for (int i = 1; i <= m; i ++)
		if (!vis[1][i]) dfs(1, i);
	for (int i = 1; i <= m; i ++)
		if (!vis[n][i]) cnt ++;
	if (cnt)
	{
		printf("0\n%d", cnt);
		return 0;
	}
	int left = 1;
	while (left <= m)
	{
		int maxr = -1e9;
		for (int i = 1; i <= m; i ++)
			if (l[1][i] <= left) maxr = max(maxr, r[1][i]);
		left = maxr + 1;
		cnt ++;
	}
	printf("1\n%d", cnt);
	return 0;
}