卷积神经网络入门
从DFT到FFT及其快速计算卷积上的代码实现,并搭建卷积神经网络
ps:原始代码来自https://www.ruanx.net/cheat-neural-network/。本文主要是在这个微型神经网络的基础上加点卷积成分。
傅里叶变换(Fourier Transform)是一种重要的数学工具,用于将时间域或空间域的信号转换到频域,揭示信号中的频率成分。它在信号处理、图像处理、通信系统、控制理论和其他许多领域中有着广泛的应用。
傅里叶变换的基本思想是将一个信号分解成正弦波和余弦波的叠加,每个波对应一个特定的频率。通过这种分解,可以将原始信号表示为这些频率成分的加权和,从而分析信号的频谱特性。
先给出傅里叶变换的公式:
傅里叶逆变换的公式:
中含有_ _,意味着要利用复平面来理解,同时,由于对t进行从无穷到无穷的积分,可以将视作一个顺时针转无数个圈的“欧拉转盘”。若f(t) = sin(3t),当且仅当w=3时,F(w) != 0;否则,由于能够转无数个圈,缠绕图像必定关于原点中心对称,最终导致积分为0;仅当w=3时,整个旋转图像呈现一个特殊的圆形,它的中心点不在原点。
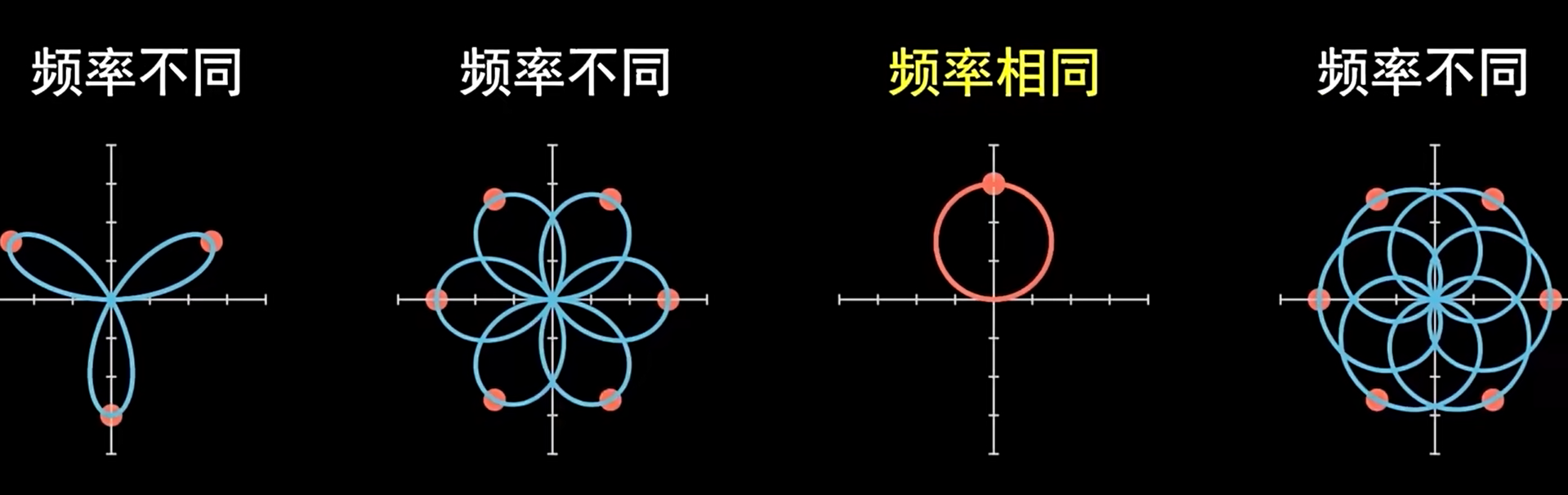
傅里叶变换将信号从时域转变为频域,从函数上来看,也就是将自变量 (时间)转为了自变量 (角速度,)。f(t)就是t时刻信号的振幅,获得的F(w)是整个信号在w对应频率下的振幅和相位。依靠复数的特性,F(w)的模长对应振幅,幅角对应相位。于是整个傅里叶变换的过程并没有产生信息的损失——它是可逆的。
而考虑实际应用,这个理论公式基本用不上。由于信号往往是通过采样获得的,因此离散条件下的傅里叶变换更为常用:
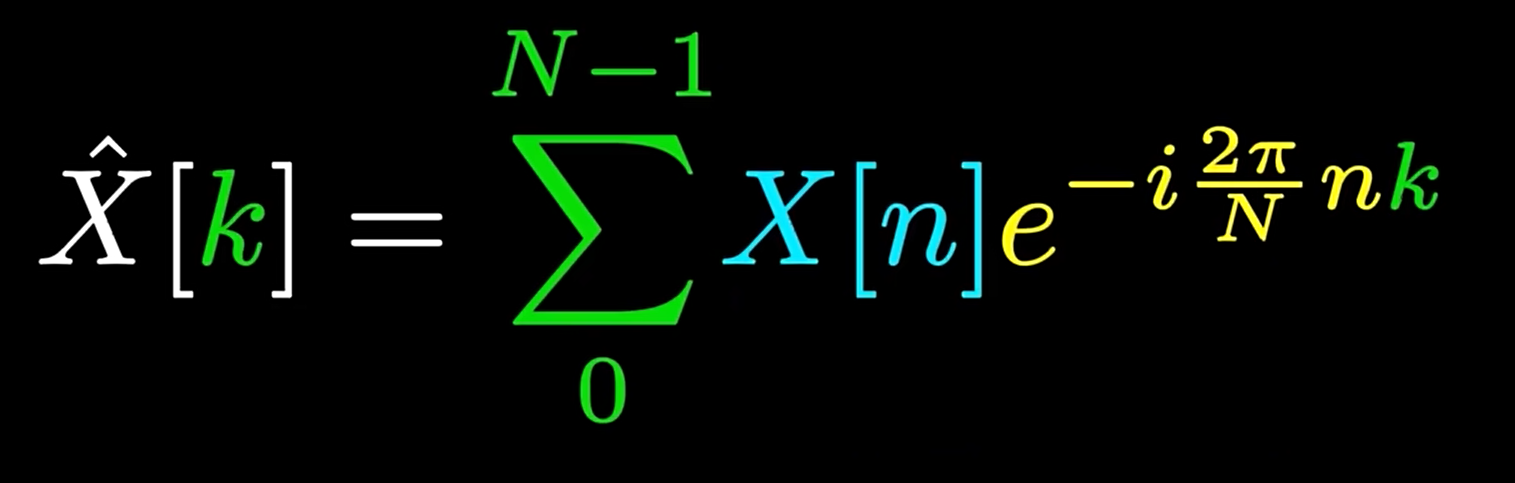
欧拉转盘并没有改变被分析的函数或矢量,而只是改变了旋转角。在公式中,k表示欧拉转盘的频率,黄色部分表示经过转盘调整后的旋转角。这样,我们将连续地旋转替换为了矢量内积:
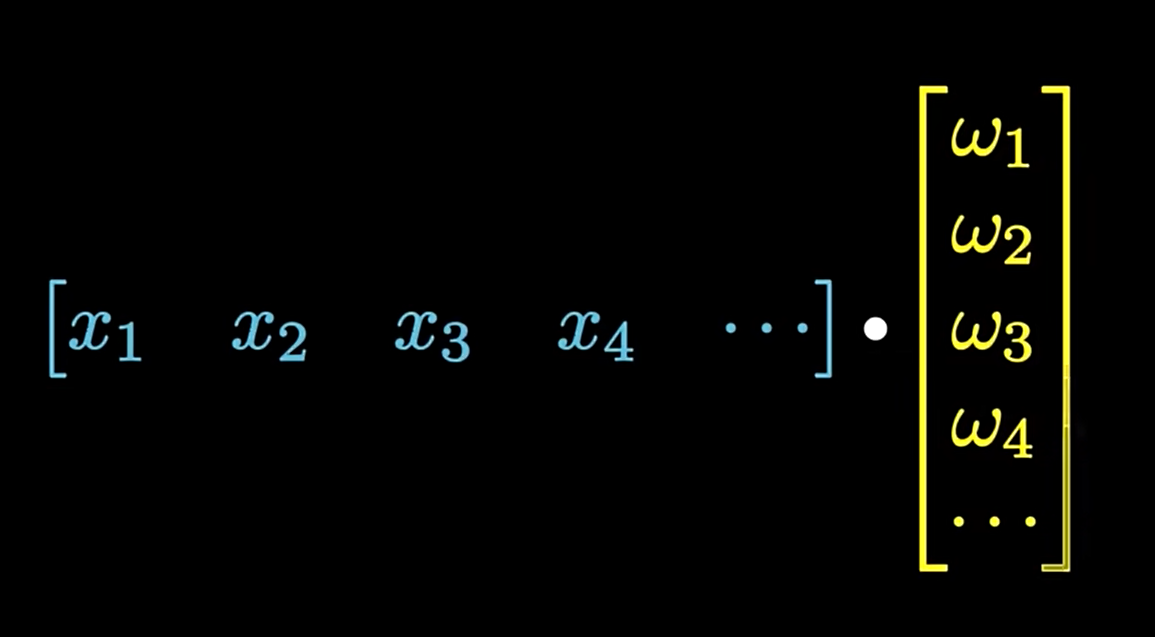
X[k]的长度一般设为与N相同。这个时候整个DFT可以视作一种矩阵乘法。
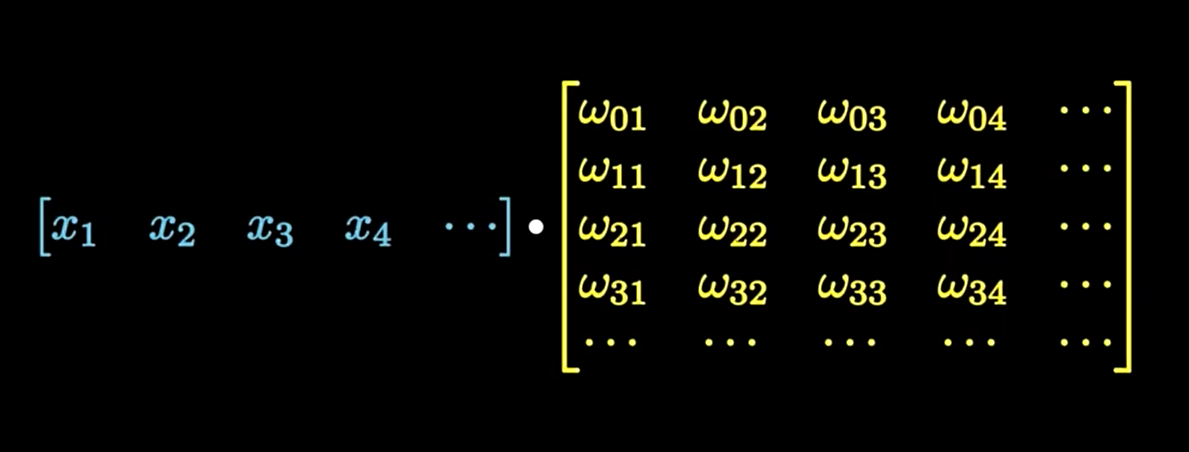
一般的傅里叶变换需要O(n^2)的时间复杂度,而快速傅里叶变换(FFT)将时间复杂度降为了O(nlogn)。下面先讲讲与FFT密切相关的:多项式相乘的优化算法。
考虑两个一般多项式的相乘,我们的乘法一般会花费O(n^2)的时间复杂度:用列表表示每一项的系数,然后进行离散上的卷积。
但事实上,一个多项式可以转变为一个偶函数和一个奇函数的和,已知n+1个点确定n次多项式,我们只需要知道(n+1)/2个点的值就可以利用奇偶性求解;而这个过程是可递归的,因此时间复杂度下降到了O(nlogn)。
FFT利用了与多项式乘法类似的分解和递归思想,用于高效计算DFT。具体来说,FFT算法通过将原始信号分解为奇数和偶数项,然后递归地计算频谱,最终合并结果。这一过程与多项式的递归分解非常相似,将输入信号 x[n]x[n] 分解为奇数项和偶数项:分别计算奇数项和偶数项的DFT(这里使用递归),合并奇数项和偶数项的DFT,得到最终的FFT结果,代码实现如下:
import numpy as np
def fft(x):
N = len(x)
if N <= 1:
return x
even = fft(x[0::2])
odd = fft(x[1::2])
T = [np.exp(-2j * np.pi * k / N) * odd[k] for k in range(N // 2)]
return [even[k] + T[k] for k in range(N // 2)] + [even[k] - T[k] for k in range(N // 2)]
# 示例输入
#x = np.random.random(8)
x = [1,2,3,4]
X = fft(x)
# 检查结果
print("输入信号: ", x)
print("FFT结果: ", X)
print("FFT模长: ", np.abs(X))
print("FFT幅角: ", np.angle(X))
输出如下:
我们理解了FFT,接下来讨论它在快速计算卷积上的利用。前面已经提到,多项式相乘可以用卷积进行计算,而类FFT的做法就将其进行了优化;我们引申出一个著名的定理:
频域卷积定理(Convolution Theorem)
频域卷积定理揭示了卷积和乘积之间的关系。具体地,它指出:
时域中的卷积对应于频域中的乘积。
时域中的乘积对应于频域中的卷积。
数学表达
设F(ω)和G(ω)分别是f(t)和g(t)的傅里叶变换,那么:
卷积定理:
F{f(t)∗g(t)}=F(ω)⋅G(ω)
乘积定理:
F{f(t)⋅g(t)}=1/2π(F(ω)∗G(ω))
其中,F表示傅里叶变换。
以下是证明过程:
证明卷积定理前,先对证明中用到的性质进行简单介绍。
傅立叶变换的时移性质。该性质表述为:设、为实常数,若,则
傅立叶变换的时移性质表明当一个信号沿时间轴平移后,各频率成份的大小不发生改变,但相位发生变化。该性质可以由傅立叶变换的定义进行证明:
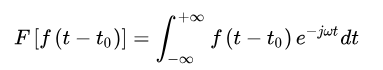
令,则有
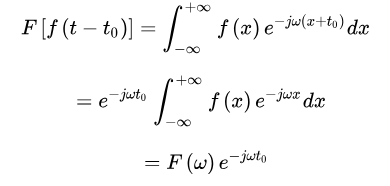
另外,由富比尼定理可知,积分区域连续的前提下,二重积分的积分次序可以交换。
下面对时域卷积定理和频域卷积定理进行推导证明。
时域定理证明
首先,卷积定义为
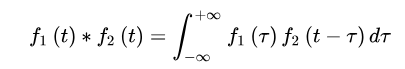
然后,代入傅立叶变换公式
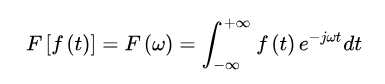
由此可得
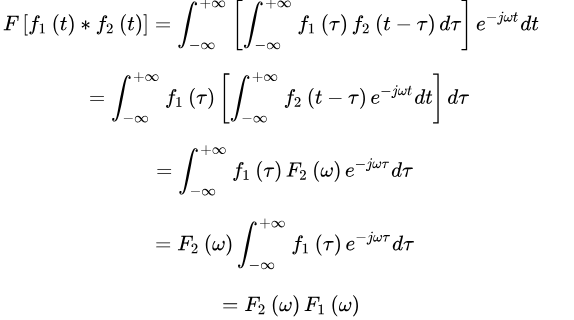
至此,时域卷积定理得证 [1]。
频域定理证明
设:
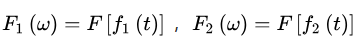
IF表示傅立叶逆变换,则
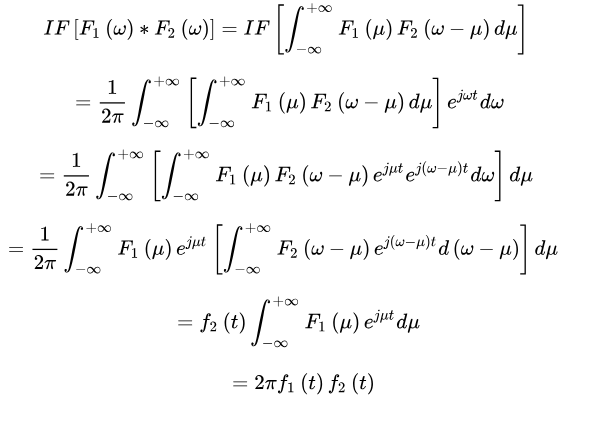
因此有
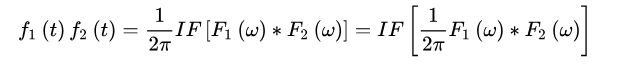
故频域卷积定理得证。
因此我们找到了一个快速计算卷积的方法,接下来我们用代码实现。
先定义一个IFFT函数:
def ifft(x):
N = len(x)
if N <= 1:
return x
even = ifft(x[0::2])
odd = ifft(x[1::2])
T = [np.exp(2j * np.pi * k / N) * odd[k] for k in range(N // 2)]
return [(even[k] + T[k]) / 2 for k in range(N // 2)] + [(even[k] - T[k]) / 2 for k in range(N // 2)]
再定义一个快速卷积函数:
def fft_convolution(signal1, signal2):
# 确定卷积结果的长度
n = len(signal1) + len(signal2) - 1
# 将信号零填充到相同长度的最小2的幂
N = 1
while N < n:
N *= 2
signal1_padded = np.pad(signal1, (0, N - len(signal1)), 'constant')
signal2_padded = np.pad(signal2, (0, N - len(signal2)), 'constant')
# 计算信号的FFT
fft_signal1 = fft(signal1_padded)
fft_signal2 = fft(signal2_padded)
# 在频域中相乘
fft_product = [a * b for a, b in zip(fft_signal1, fft_signal2)]
# 计算IFFT以获得卷积结果
convolution_result = ifft(fft_product)
# 截断零填充的部分
convolution_result = convolution_result[:n]
return convolution_result
测试数据:
# 示例输入
#x = np.random.random(8)
x = [1,2,3,4]
X = fft(x)
x2 = ifft(X)
# 检查结果
print("输入信号: ", x)
print("FFT结果: ", X)
print("FFT模长: ", np.abs(X))
print("FFT幅角: ", np.angle(X))
print("IFFT结果: ", np.abs(x2))
y1 = [1,2,3,4,5,6,7,8,9]
y2 = [9,8,7,6,5,4,3,2,1]
print(np.abs(fft_convolution(y1,y2)))
输出结果:
掌握了快速卷积算法的原理,我们就可以考虑将其运用在神经网络当中了。
MNIST数据集是一个经典的机器学习数据集,包含60,000张28x28像素的手写数字图片和10,000张测试图片,广泛用于图像分类任务和新手练习。
用pytorch写出一个简单的神经网络:
import sys
sys.path.append('/home/aistudio/external-libraries')
import torch
import torchvision
import torch.nn as nn
import torchvision.transforms as transforms
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
trans_to_tensor = transforms.Compose([
transforms.ToTensor()
])
# 加载MNIST训练数据集
data_train = torchvision.datasets.MNIST(
'./mnist_data', # 数据存储路径
train=True, # 指定为训练数据集
transform=trans_to_tensor, # 应用预处理转换
download=True # 如果数据集不存在,则下载
)
# 加载MNIST测试数据集
data_test = torchvision.datasets.MNIST(
'./mnist_data', # 数据存储路径
train=False, # 指定为测试数据集
transform=trans_to_tensor, # 应用预处理转换
download=True # 如果数据集不存在,则下载
)
# 创建数据加载器,将训练数据分成批次,每批次包含100个样本,且每次迭代时打乱数据顺序
train_loader = torch.utils.data.DataLoader(
data_train,
batch_size=100,
shuffle=True
)
# 定义一个简单的神经网络类,继承自nn.Module
class MyNet(nn.Module):
# 初始化函数,定义网络的层次结构
def __init__(self):
super().__init__()
# 定义第一个全连接层,将输入的28x28的图像展平到100维
self.fc1 = nn.Linear(28*28, 100)
# 定义第二个全连接层,将100维的输入转换到10维的输出
self.fc2 = nn.Linear(100, 10)
# 前向传播函数,定义数据如何通过网络
def forward(self, x):
# 将输入x展平成1维向量(大小为28x28)
x = x.view(-1, 28*28)
# 通过第一个全连接层
x = self.fc1(x)
# 使用ReLU激活函数
x = F.relu(x)
# 通过第二个全连接层
x = self.fc2(x)
# 使用sigmoid激活函数
x = torch.sigmoid(x)
return x
# 创建网络实例
net = MyNet()
# 定义设备为CPU
device = torch.device('cpu')
# 将网络移动到设备上
net.to(device)
# 定义损失函数为交叉熵损失
criterion = nn.CrossEntropyLoss()
# 定义优化器为Adam,并传入网络的参数
optimizer = torch.optim.Adam(net.parameters())
# 定义测试函数,用于评估模型的性能
def test(net):
# 设置模型为评估模式
net.eval()
# 创建测试数据加载器,不打乱数据,批次大小为10000
test_loader = torch.utils.data.DataLoader(data_train, batch_size=10000, shuffle=False)
test_data = next(iter(test_loader))
# 禁用梯度计算
with torch.no_grad():
x, y = test_data[0].to(device), test_data[1].to(device)
# 前向传播,得到模型输出
outputs = net(x)
# 获取预测结果
pred = torch.max(outputs, 1)[1]
# 打印测试准确率
print(f'test acc: {sum(pred == y) / outputs.shape[0]}')
# 恢复模型为训练模式
net.train()
# 定义训练函数,用于训练模型
def fit(net, epoch=1):
# 设置模型为训练模式
net.train()
run_loss = 0
# 迭代每个训练周期
for num_epoch in range(epoch):
print(f'epoch {num_epoch}')
# 迭代每个数据批次
for i, data in enumerate(train_loader):
x, y = data[0].to(device), data[1].to(device)
# 前向传播,得到模型输出
outputs = net(x)
# 计算损失
loss = criterion(outputs, y)
# 清零梯度
optimizer.zero_grad()
# 反向传播
loss.backward()
# 更新参数
optimizer.step()
# 累计运行损失
run_loss += loss.item()
# 每100个批次打印一次损失并进行测试
if i % 100 == 99:
print(f'[{i+1} / 600] loss={run_loss / 100}')
run_loss = 0
test(net)
# 运行训练函数,设置训练周期为5
fit(net, epoch=5)
最终测试结果为:
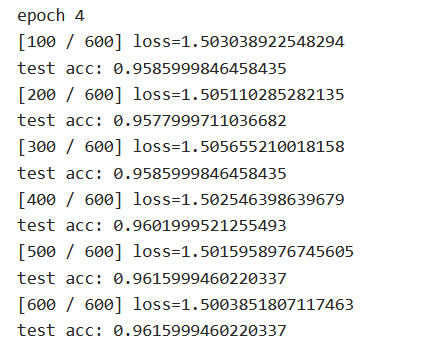
准确率达到了96.159%。接下来我们将其改造为卷积神经网络,看看经过卷积后,它的准确率能否被提高。
Pytorch很方便地为我们准备了.Conv2d函数来进行卷积操作。
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=5, stride=1, padding=0) # 卷积层:输入通道1,输出通道16,卷积核大小5x5
self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2) # 最大池化层,核大小为2,步幅为2,将图像大小变为原来的1/4(1/2*1/2 = 1/4)
self.conv2 = nn.Conv2d(in_channels=16, out_channels=36, kernel_size=3, stride=1, padding=0) # 卷积层2:输入通道16,输出通道32,卷积核大小3x3
self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2) # 最大池化层2
# 定义第一个全连接层,将输入的36x5x5的图像展平到100维
self.fc1 = nn.Linear(36*5*5, 100)
# 定义第二个全连接层,将100维的输入转换到10维的输出
self.fc2 = nn.Linear(100, 10)
def forward(self, x):
# 卷积层1 -> 激活函数(relu) -> 池化层1
x = self.pool1(F.relu(self.conv1(x)))
x = self.pool2(F.relu(self.conv2(x)))
# 将输入x展平成1维向量,大小为36x5x5
x = x.view(-1, 36*5*5)
# 通过第一个全连接层
x = self.fc1(x)
# 使用ReLU激活函数
x = F.relu(x)
# 通过第二个全连接层
x = self.fc2(x)
# 使用sigmoid激活函数
x = torch.sigmoid(x)
return x

使用卷积神经网络,准确率显著提升到了98.580%。
至此,我们成功将积分变换中的卷积应用在神经网络的搭建上,并显著提高了它的识别能力。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号