可持久化线段树

1. 基本概念

• 线段树（Segment Tree）：用于高效的区间查询和更新。
• 可持久化：每次对数据结构的修改（如添加、删除或更新）都会创建一个新版本，该版本与之前的版本共享大部分结构。

2. 概述

可持久化线段树最大的特点是：可以访问历史版本。例如，我对线段树进行了1000次修改操作，突然问你第233次修改之后某个区间的区间和是多少——这个问题可持久化线段树就可以正常地回答出来。这个性质有许多奇妙的应用。

那么如何实现这样的一棵线段树呢？

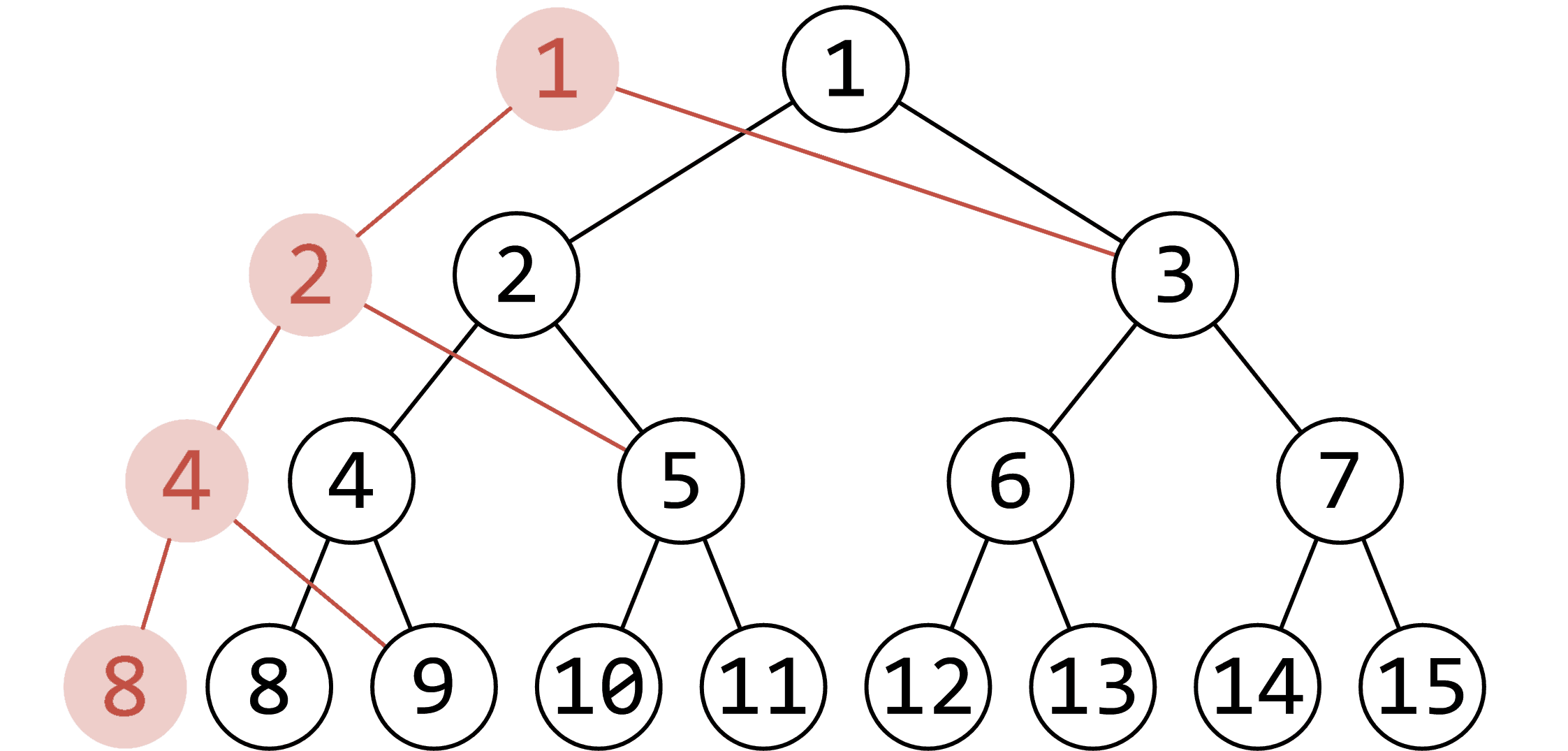
想象一棵普通的线段树，我们要对它进行单点修改，需要修改\(log(n)\)个点。每次修改的时候，我们丝毫不修改原来的节点，而是在它旁边新建一个节点，把原来节点的信息（如左右儿子编号、区间和等）复制到新节点上，并对新节点进行修改。

那么如何查询历史版本呢？只需记录每一次修改对应的新根节点编号（根据上面描述的操作，根节点每次一定会新建一个的），每次询问从对应的根节点往下查询就好了。

3. 构建线段树

构建线段树的过程与普通线段树相似，但我们需要注意节点的创建和管理。

int build(int l, int r) {  // 建树
  int root = ++tot;
  if (l == r) return root;
  int mid = l + r >> 1;
  ls[root] = build(l, mid);
  rs[root] = build(mid + 1, r);
  return root;  // 返回该子树的根节点
}

4. 更新操作

更新操作需要返回一个新的节点，而不是直接修改现有节点。我们采用复制策略，在修改的过程中只复制必要的节点。

int update(int k, int l, int r, int root) {  // 插入操作
  int dir = ++tot;
  ls[dir] = ls[root], rs[dir] = rs[root], sum[dir] = sum[root] + 1;
  if (l == r) return dir;
  int mid = l + r >> 1;
  if (k <= mid)
    ls[dir] = update(k, l, mid, ls[dir]);
  else
    rs[dir] = update(k, mid + 1, r, rs[dir]);
  return dir;
}

5. 查询操作

查询操作相对简单，可以直接从当前节点开始递归查询。

int query(int u, int v, int l, int r, int k) {  // 查询操作
  int mid = l + r >> 1,
      x = sum[ls[v]] - sum[ls[u]];  // 通过区间减法得到左儿子中所存储的数值个数
  if (l == r) return l;
  if (k <= x)  // 若 k 小于等于 x ，则说明第 k 小的数字存储在在左儿子中
    return query(ls[u], ls[v], l, mid, k);
  else  // 否则说明在右儿子中
    return query(rs[u], rs[v], mid + 1, r, k - x);
}

6. 使用示例

#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 1e5;  // 数据范围
int tot, n, m;
int sum[(maxn << 5) + 10], rt[maxn + 10], ls[(maxn << 5) + 10],
    rs[(maxn << 5) + 10];
int a[maxn + 10], ind[maxn + 10], len;

int getid(const int &val) {  // 离散化
  return lower_bound(ind + 1, ind + len + 1, val) - ind;
}

int build(int l, int r) {  // 建树
  int root = ++tot;
  if (l == r) return root;
  int mid = l + r >> 1;
  ls[root] = build(l, mid);
  rs[root] = build(mid + 1, r);
  return root;  // 返回该子树的根节点
}

int update(int k, int l, int r, int root) {  // 插入操作
  int dir = ++tot;
  ls[dir] = ls[root], rs[dir] = rs[root], sum[dir] = sum[root] + 1;
  if (l == r) return dir;
  int mid = l + r >> 1;
  if (k <= mid)
    ls[dir] = update(k, l, mid, ls[dir]);
  else
    rs[dir] = update(k, mid + 1, r, rs[dir]);
  return dir;
}

int query(int u, int v, int l, int r, int k) {  // 查询操作
  int mid = l + r >> 1,
      x = sum[ls[v]] - sum[ls[u]];  // 通过区间减法得到左儿子中所存储的数值个数
  if (l == r) return l;
  if (k <= x)  // 若 k 小于等于 x ，则说明第 k 小的数字存储在在左儿子中
    return query(ls[u], ls[v], l, mid, k);
  else  // 否则说明在右儿子中
    return query(rs[u], rs[v], mid + 1, r, k - x);
}

void init() {
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; ++i) scanf("%d", a + i);
  memcpy(ind, a, sizeof ind);
  sort(ind + 1, ind + n + 1);
  len = unique(ind + 1, ind + n + 1) - ind - 1;
  rt[0] = build(1, len);
  for (int i = 1; i <= n; ++i) rt[i] = update(getid(a[i]), 1, len, rt[i - 1]);
}

int l, r, k;

void work() {
  while (m--) {
    scanf("%d%d%d", &l, &r, &k);
    printf("%d\n", ind[query(rt[l - 1], rt[r], 1, len, k)]);  // 回答询问
  }
}

int main() {
  init();
  work();
  return 0;
}