304. Range Sum Query 2D - Immutable

 

Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

 

 

Approach #3 (Caching Rows) [Accepted]
Intuition

Remember from the 1D version where we used a cumulative sum array? Could we apply that directly to solve this 2D version?

Algorithm

Try to see the 2D matrix as mm rows of 1D arrays. To find the region sum, we just accumulate the sum in the region row by row.

private int[][] dp;

public NumMatrix(int[][] matrix) {
    if (matrix.length == 0 || matrix[0].length == 0) return;
    dp = new int[matrix.length][matrix[0].length + 1];
    for (int r = 0; r < matrix.length; r++) {
        for (int c = 0; c < matrix[0].length; c++) {
            dp[r][c + 1] = dp[r][c] + matrix[r][c];
        }
    }
}

public int sumRegion(int row1, int col1, int row2, int col2) {
    int sum = 0;
    for (int row = row1; row <= row2; row++) {
        sum += dp[row][col2 + 1] - dp[row][col1];
    }
    return sum;
}
Complexity analysis

Time complexity : O(m)time per query, O(mn)time pre-computation. The pre-computation in the constructor takes O(mn) time. The sumRegion query takes O(m)time.

Space complexity : O(mn). The algorithm uses O(mn) space to store the cumulative sum of all rows.

Approach #4 (Caching Smarter) [Accepted]

Algorithm

We used a cumulative sum array in the 1D version. We notice that the cumulative sum is computed with respect to the origin at index 0. Extending this analogy to the 2D case, we could pre-compute a cumulative region sum with respect to the origin at (0, 0)(0,0).

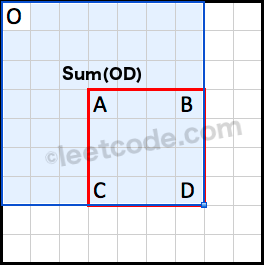
Sum(OD) is the cumulative region sum with respect to the origin at (0, 0).

How do we derive Sum(ABCD)Sum(ABCD) using the pre-computed cumulative region sum?

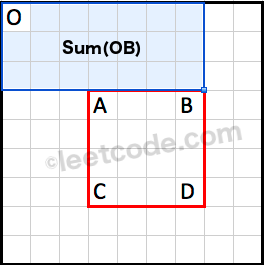
Sum(OB) is the cumulative region sum on top of the rectangle.

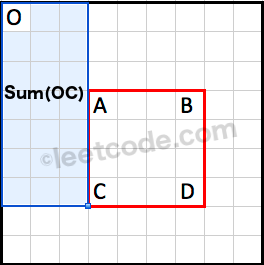
Sum(OC) is the cumulative region sum to the left of the rectangle.

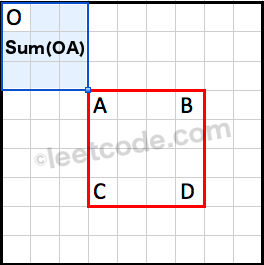
Sum(OA) is the cumulative region sum to the top left corner of the rectangle.

Note that the region Sum(OA) is covered twice by both Sum(OB) and Sum(OC). We could use the principle of inclusion-exclusion to calculate Sum(ABCD) as following:

 

Sum(ABCD) = Sum(OD) - Sum(OB) - Sum(OC) + Sum(OA)   

private int[][] dp;

public NumMatrix(int[][] matrix) {
    if (matrix.length == 0 || matrix[0].length == 0) return;
    dp = new int[matrix.length + 1][matrix[0].length + 1];
    for (int r = 0; r < matrix.length; r++) {
        for (int c = 0; c < matrix[0].length; c++) {
            dp[r + 1][c + 1] = dp[r + 1][c] + dp[r][c + 1] + matrix[r][c] - dp[r][c];
        }
    }
}

public int sumRegion(int row1, int col1, int row2, int col2) {
    return dp[row2 + 1][col2 + 1] - dp[row1][col2 + 1] - dp[row2 + 1][col1] + dp[row1][col1];
}
Complexity analysis

Time complexity : O(1) time per query, O(mn)  time pre-computation. The pre-computation in the constructor takes O(mn) time. Each sumRegion query takes O(1) time.

Space complexity : O(mn). The algorithm uses O(mn) space to store the cumulative region sum.