实用指南:2. 单片机基础概述
2025-12-06 14:31 tlnshuju 阅读(0) 评论(0) 收藏 举报来自于 : https://www.stcai.com/cp_stc8hxl
国产崛起!!! 同胞们 好好学吧 为中国强大而努力!!!!!!!!
这一章主要讲述的内容有:
①在数字设备中进行算术运算的基本知识–数制和编码;
②数字电路中一些常用逻辑运算及其图形符号。它们是学习单片机这门课程的基础。
1.1 什么是单片机/微控制器
在一个芯片上实现一个完整的计算机系统就是单片微型计算机,简称单片机,俗称 MCU/微控制器当然,有些有机械件的外围,由于材料的问题无法集成,如键盘,如显示器。
1.1.1经典单片机 89C52RC/89C58RD+系列组成框图
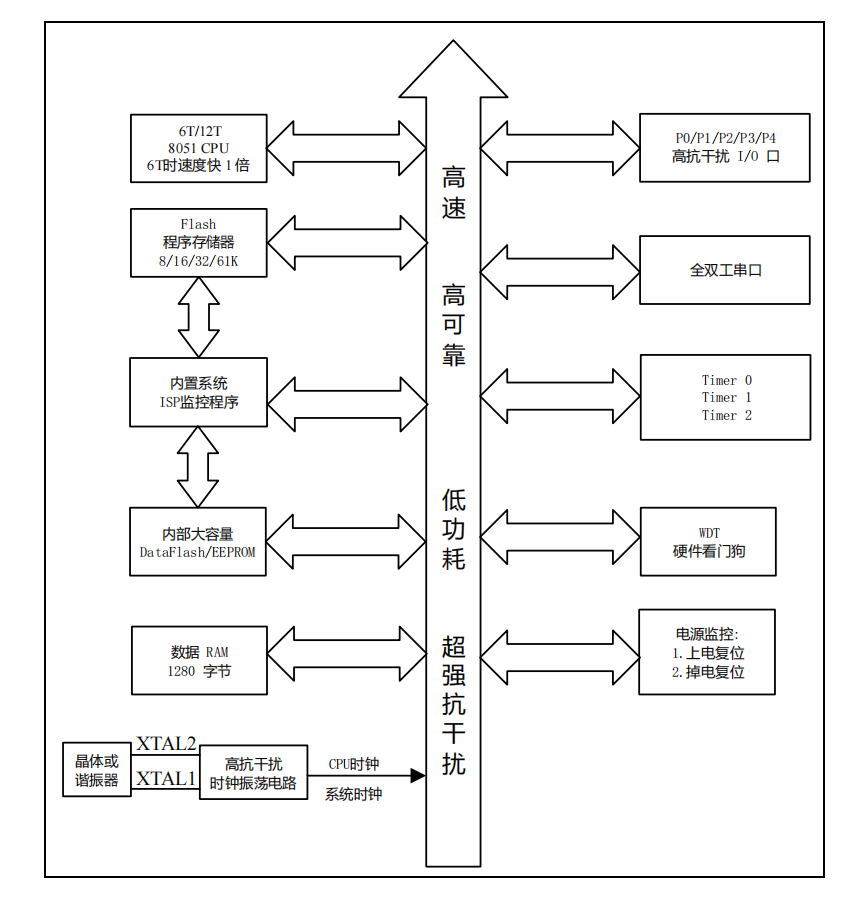
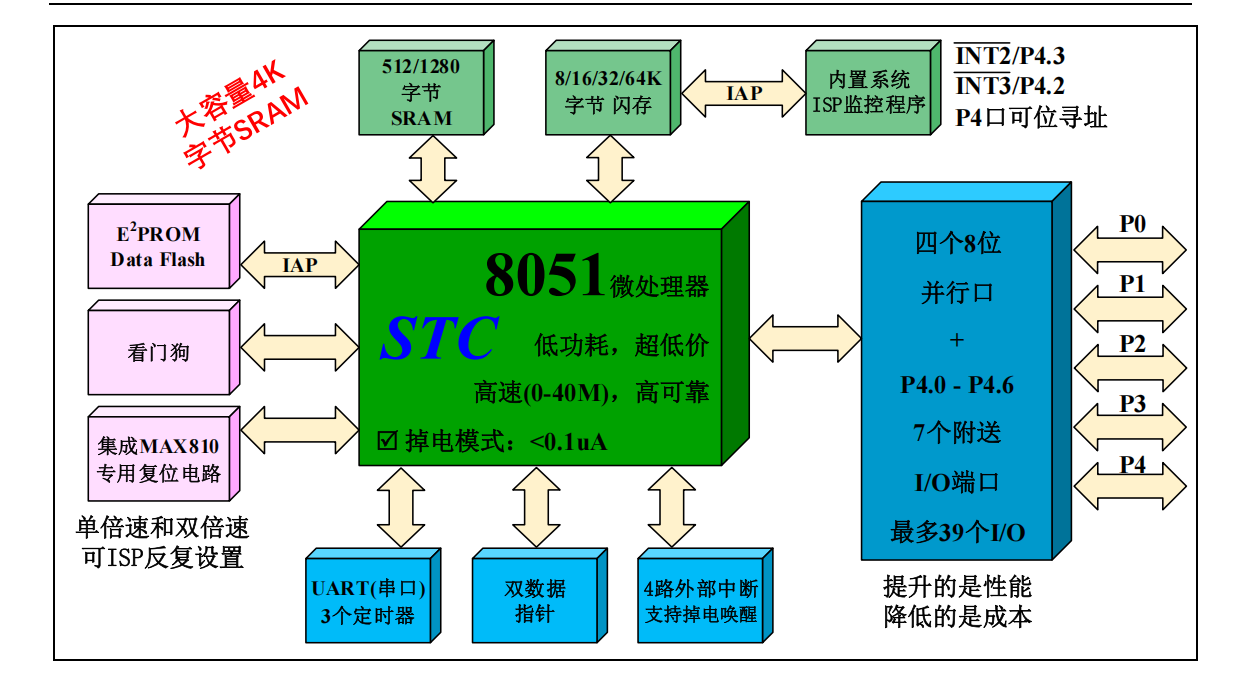
1.1.2 经典单片机 12C5A60S2组成框图
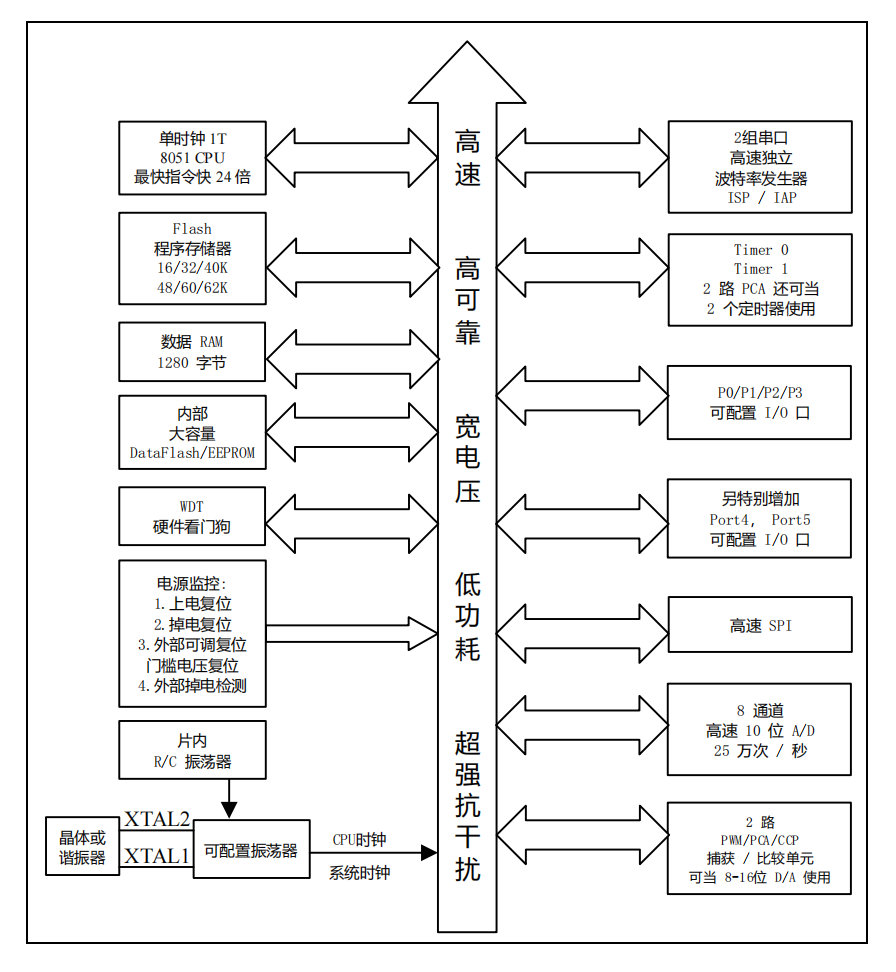
1.1.3 STC8H8K64U内部结构图
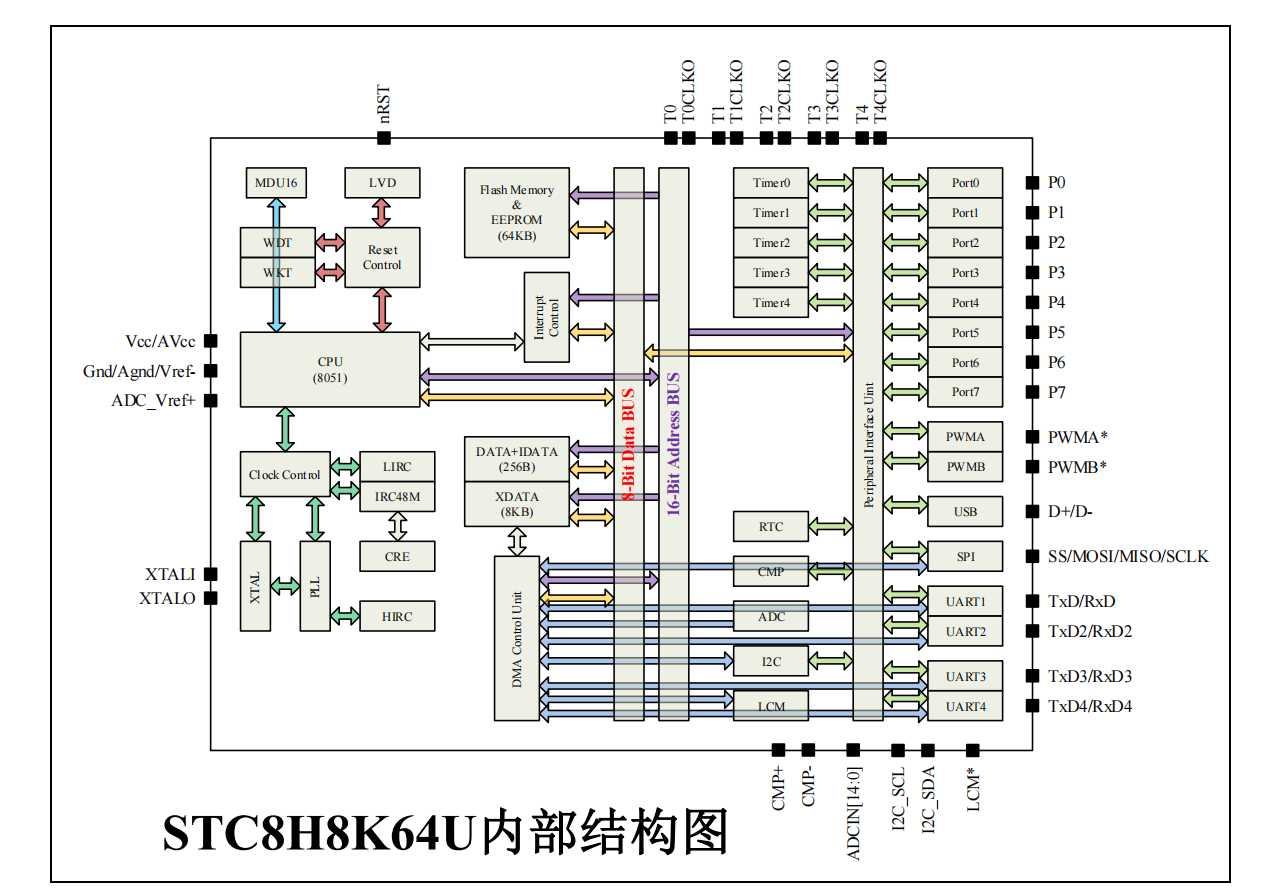
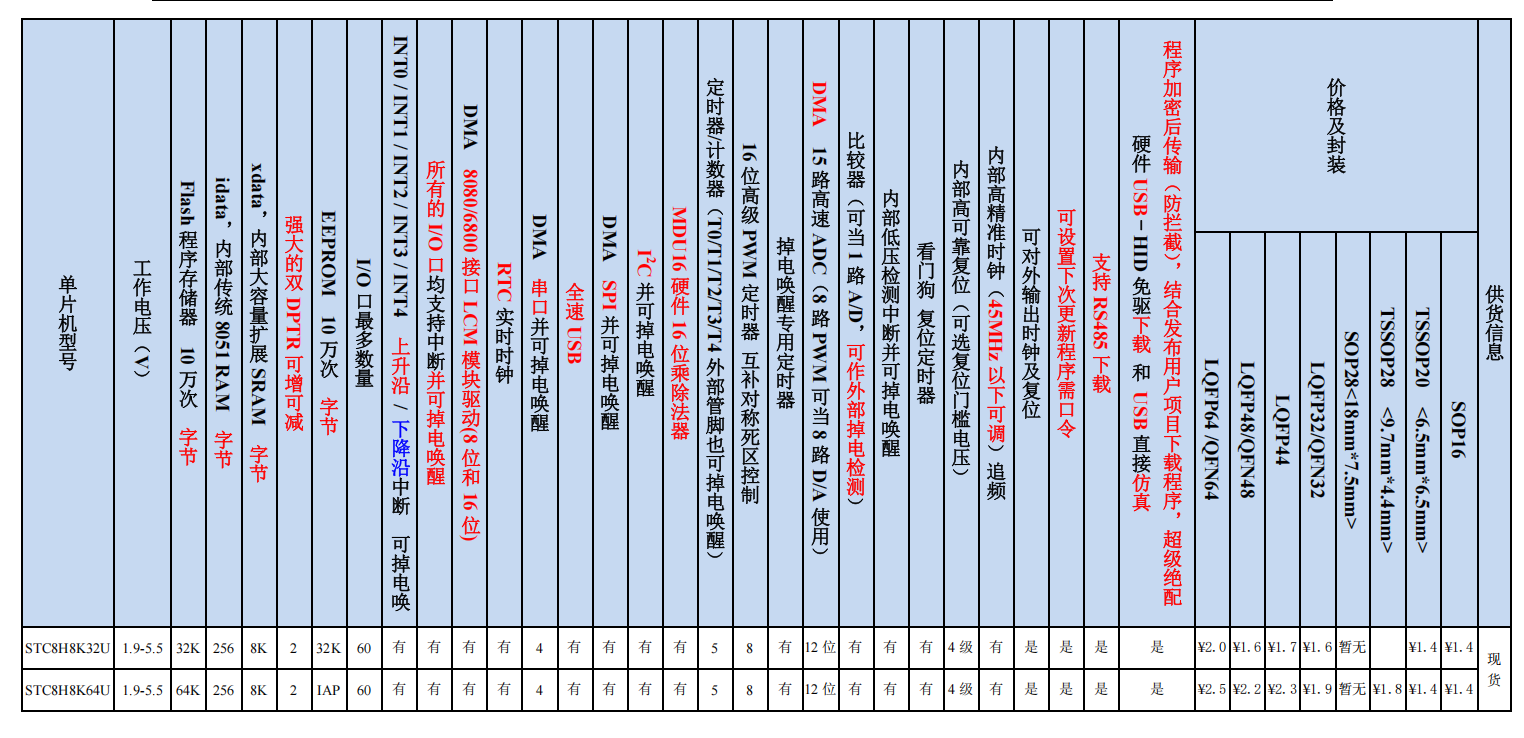
1.1.4 Ai8051U内部结构图
32 位(兼容 16/8/1 位)。就是Ai8051U 系列内部的数据总线宽度
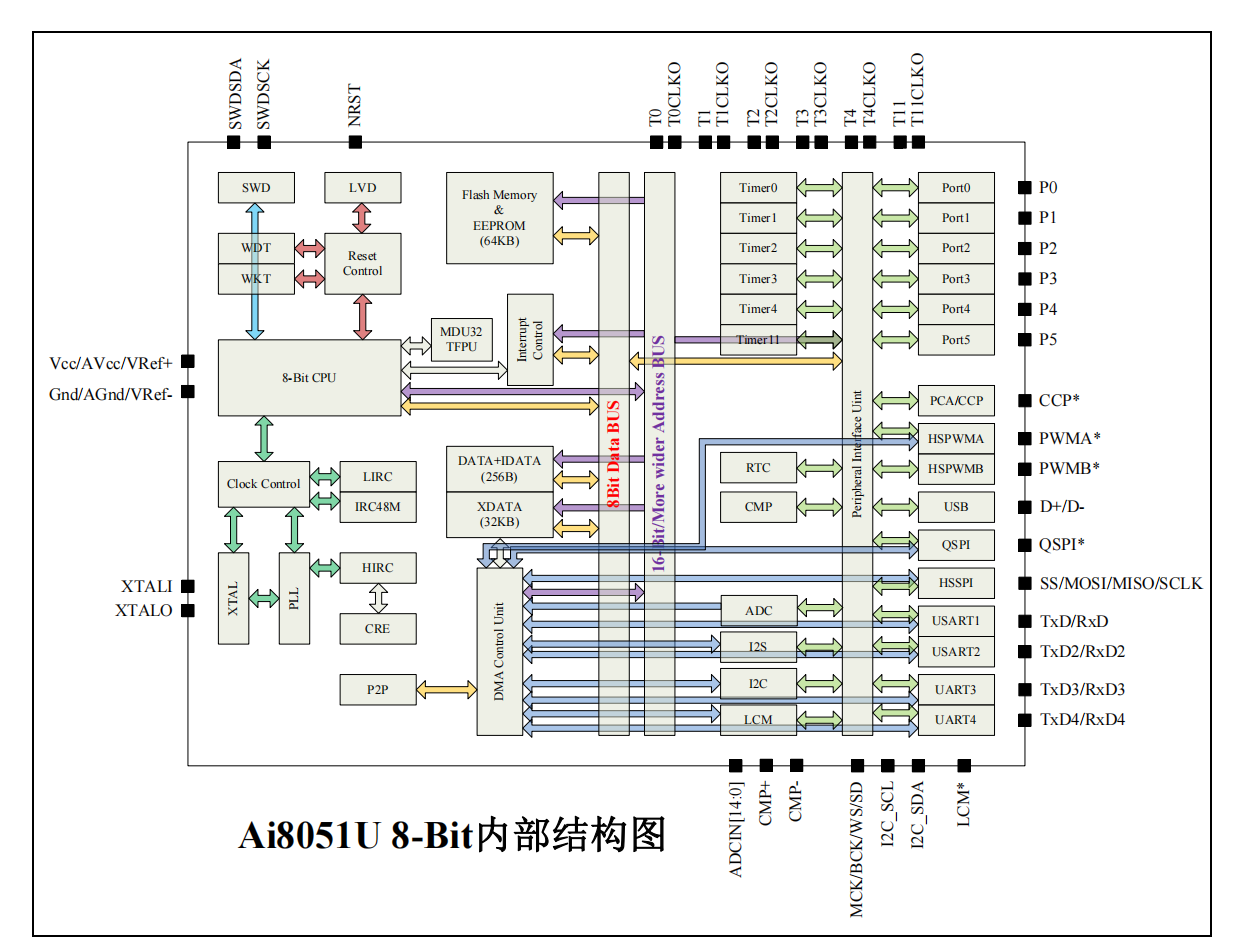
1.1.4.1 Ai8051U8-Bit内部结构图,内部总线工作在8位宽度
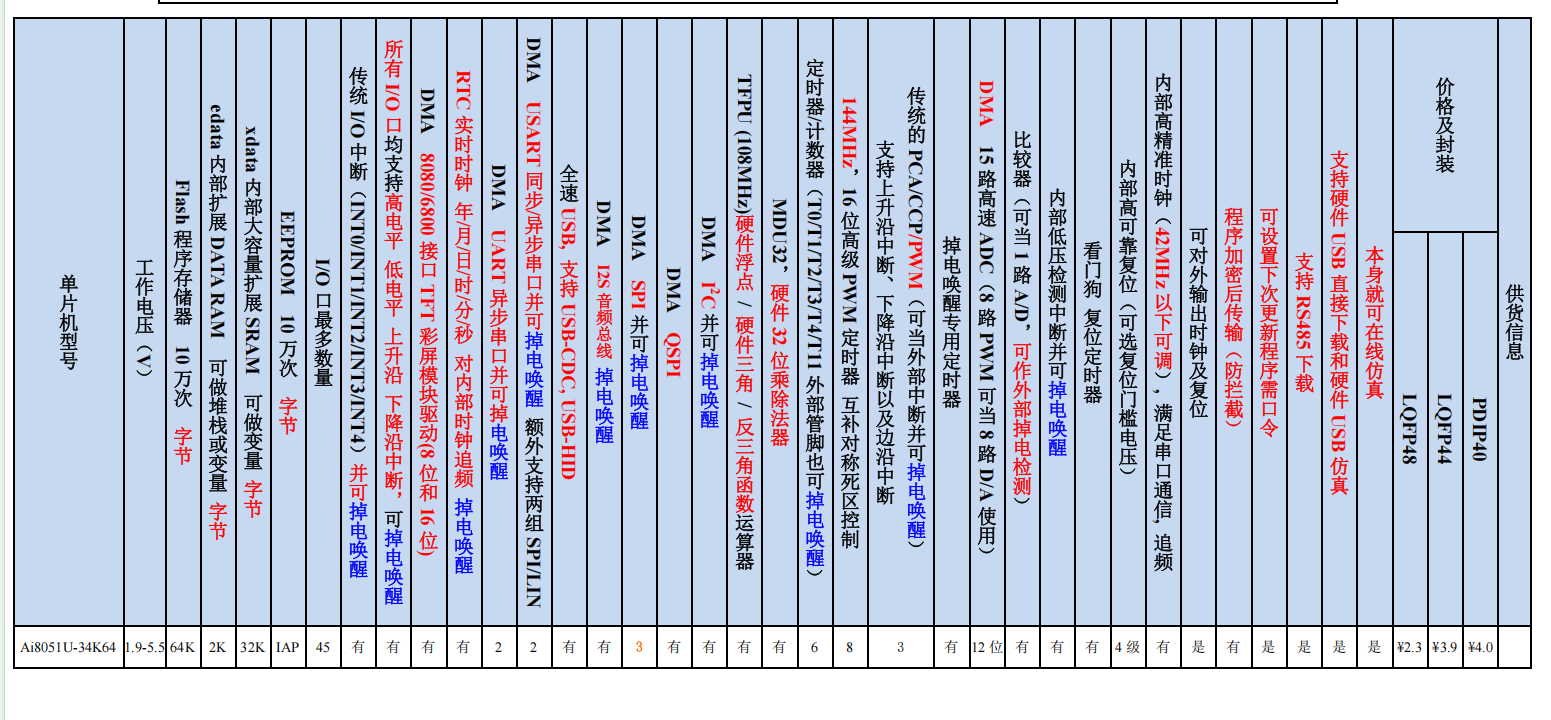
1.1.4.2 Ai8051U 32-Bit内部结构图,内部总线工作在32位宽度
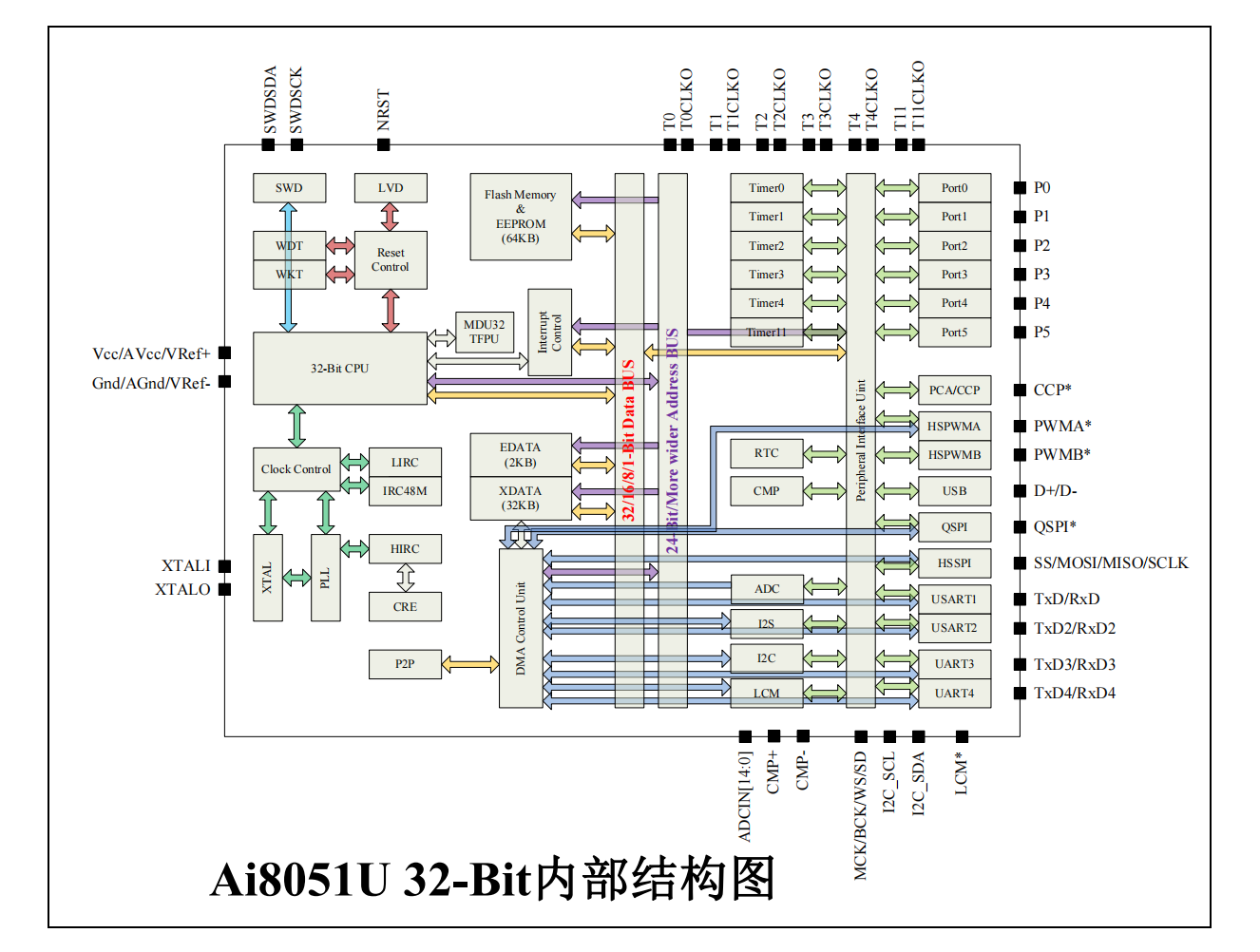
Ai8051U-32Bit 内部数据总线是 32 位宽度,从而确保 32 位的 edata 数据可以一个 CPU 时钟就可完成数据读写。而 Intel 的 80251,由于制造工艺和成本的原因,芯片内部的数据总线是8位宽度设计,同样 32位的 edata 材料的读写,Intel 的 80251 则必须读写4次,再进行数据合并。即使读1个8位字节,也是读 32 位,只是舍弃不得的 24 位即使读1个 16 位的 WORD,2 个字节,也是读 32 位,只是舍弃不需要的 16 位这样设计成本低,速度快!
Intel80251 读写 32位4个字节的数据,要分4次读写4个8位的字节,效率低。
Intel80251读写16位2个字节的数据,要分2次读写2个8位的字节,效率低。
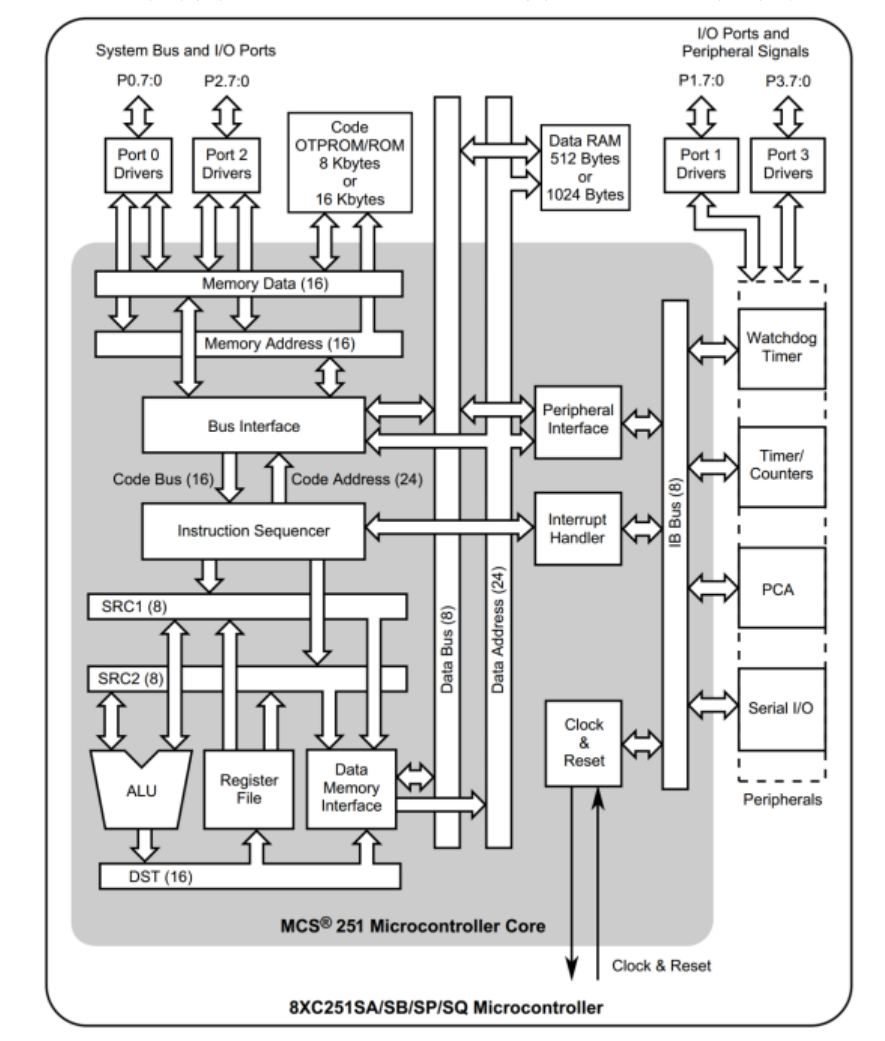
1.1.5 Intel80251内部结构图
Intel的 80251 芯片内部数据总线宽度是8位,但是 32 位指令集,号称 16 位单片机。内部结构图如下:
1.2 STC8H 单片机性能概述
- 宽电压/高速/高可靠低功耗/强抗静电/较强抗干扰的新一代 8051单片机,超级加密。指令代码完全兼容传统 8051。就是STC8H 系列单片机是不需要外部品振和外部复位的单片机,是以超强抗干扰/超低价/高速/低功耗为目标的 8051单片机,在相同的工作频率下,STC8H 系列单片机比传统的 8051约快 12 倍(速度快 11.2~13.2倍),依次按顺序执行完全部的111条指令,STC8H 系列单片机仅需 147 个时钟,而传统 8051 则需要1944 个时钟。STC8H 系列单片机是 STC 生产的单时钟/机器周期(1T)的单片机,

1.3 STC8H 单片机产品线
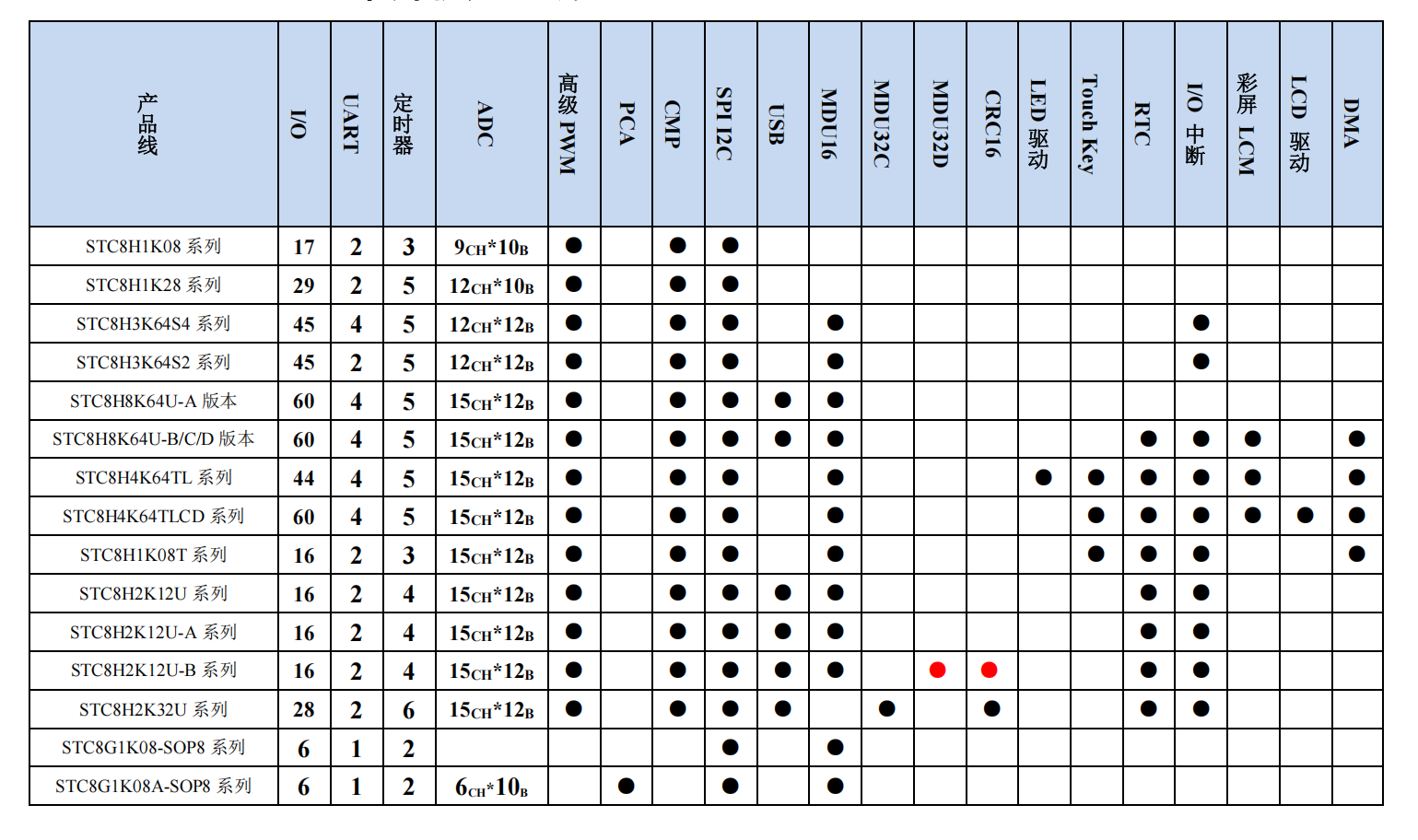
1.4 数制与编码
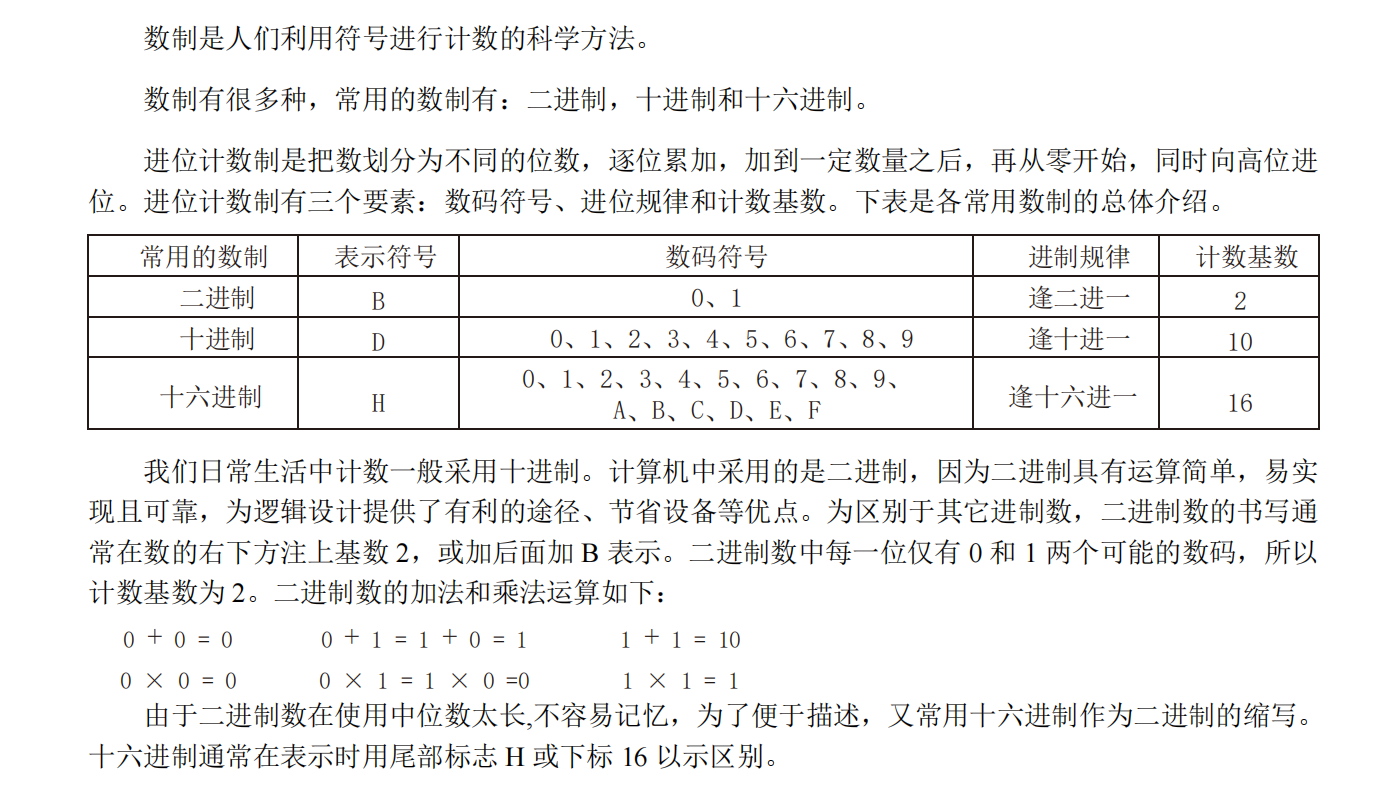


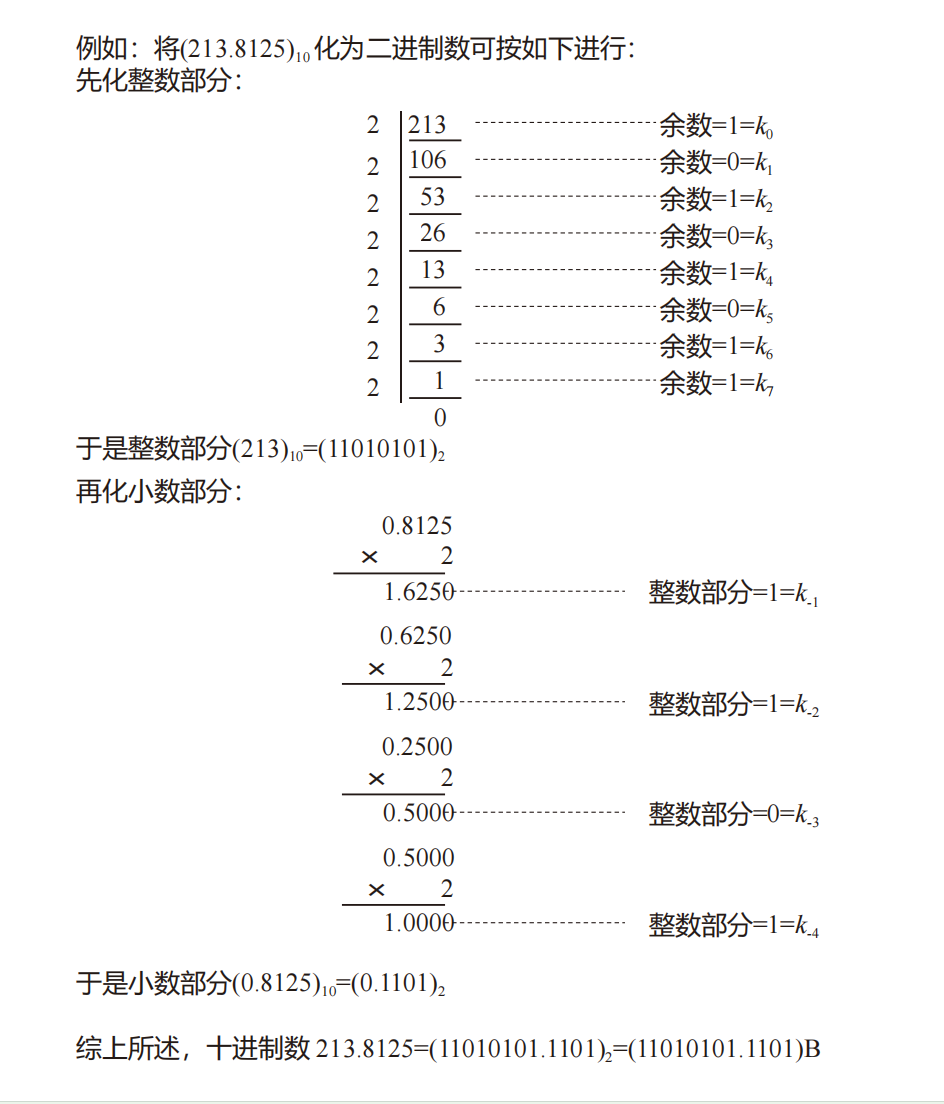


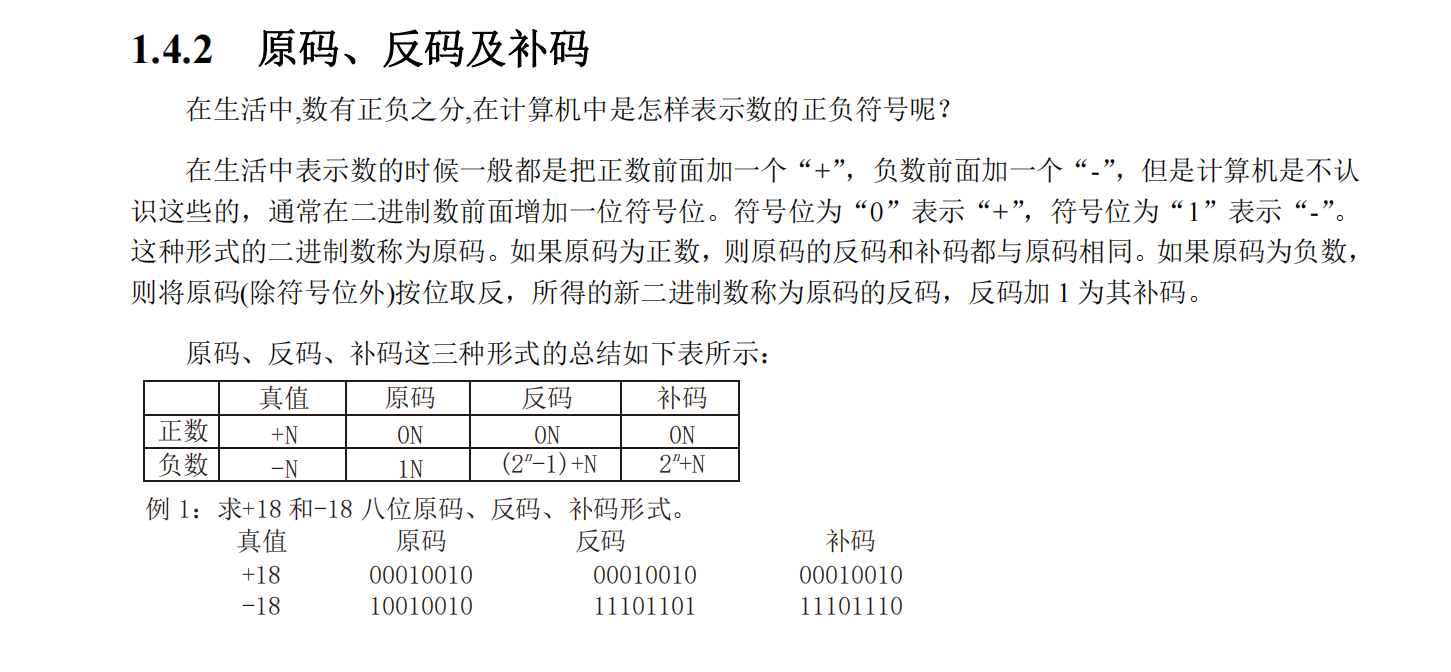
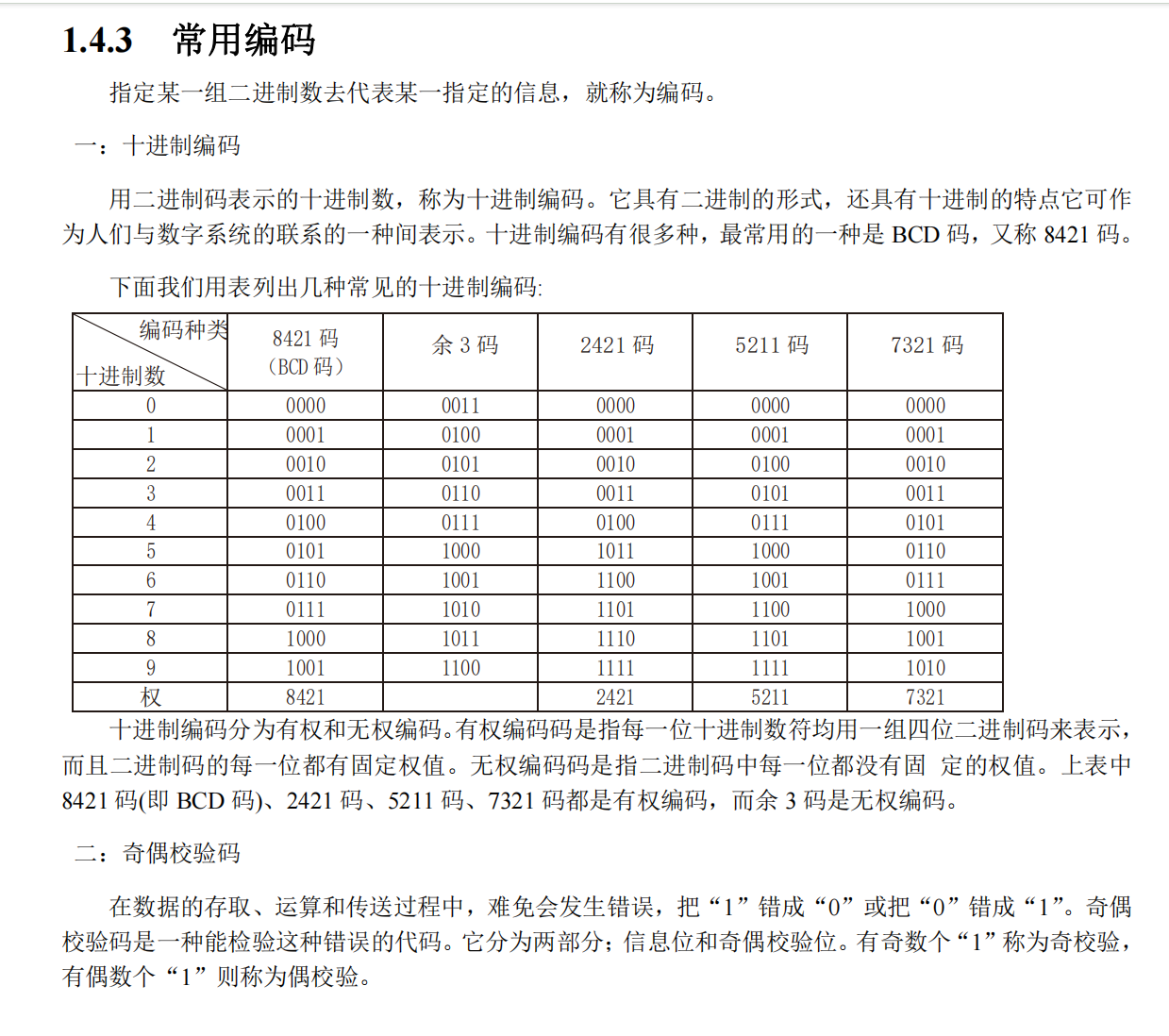
要理解编码中的“权”以及8421编码的权重逻辑,我们可以从有权编码的定义和具体编码的设计原理来分析:
一、“权”的含义
在有权编码中,“权”指的是二进制编码中每一位的固定数值权重。对于4位二进制编码的十进制数(如表格中的编码),每一位的权值相加,即可得到对应的十进制数。
二、8421码(BCD码)的权重逻辑
8421码是最常用的十进制编码,属于有权编码,其4位二进制位的权值从高位到低位依次为:
- 第1位(最高位):
8(即 (2^3)) - 第2位:
4(即 (2^2)) - 第3位:
2(即 (2^1)) - 第4位(最低位):
1(即 (2^0))
举例:十进制数5的8421编码是0101,计算方式为:
(8 \times 0 + 4 \times 1 + 2 \times 0 + 1 \times 1 = 5),与十进制数完全对应。
三、其他有权编码的权重与设计逻辑
- 2421码(权值:2、4、2、1)
- 编码规则:4位二进制位的权值从高位到低位依次为2、4、2、1。
- 示例:十进制数
5的编码是1011,计算过程为:
2×1+4×0+2×1+1×1=5 2 \times 1 + 4 \times 0 + 2 \times 1 + 1 \times 1 = 52×1+4×0+2×1+1×1=5
- 5211码(权值:5、2、1、1)
- 编码规则:4位二进制位的权值从高位到低位依次为5、2、1、1。
- 示例:十进制数
5的编码是1000,计算过程为:
5×1+2×0+1×0+1×0=5 5 \times 1 + 2 \times 0 + 1 \times 0 + 1 \times 0 = 55×1+2×0+1×0+1×0=5
- 7321码(权值:7、3、2、1)
- 编码规则:4位二进制位的权值从高位到低位依次为7、3、2、1。
- 示例:十进制数
5的编码是0110,计算过程为:
7×0+3×1+2×1+1×0=5 7 \times 0 + 3 \times 1 + 2 \times 1 + 1 \times 0 = 57×0+3×1+2×1+1×0=5
四、无权编码(以余3码为例)
余3码属于无权编码,即二进制位没有固定权值,其编码逻辑是“8421码 + 3(二进制0011)”。例如:
- 十进制
0的余3码是0011(0000 + 0011 = 0011); - 十进制
1的余3码是0100(0001 + 0011 = 0100)。
由于没有固定权值,无法通过“权值相加”直接得到十进制数,只能通过编码间的偏移关系(+3)推导。
总结
- 有权编码的“权”是每一位的固定数值权重,通过“权值×位值之和”可直接得到十进制数(如8421、2421等);
- 8421码的权重8、4、2、1最直观的二进制-十进制映射;就是,源于二进制位的幂次((2^3, 2^2, 2^1, 2^0)),
- 无权编码(如余3码)无固定权值,需借助编码间的逻辑关系(如偏移)推导十进制数。
要搞懂余3码,我们可能从它的生成规则、编码示例、特性三个维度逐步拆解,保证通俗易懂:
一、余3码的定义:“8421码 + 3”
余3码是一种无权十进制编码(没有固定位权,不能利用“位权×位值”计算十进制数),生成规则很简单:
余3码 = 对应的8421 BCD码 + 3(二进制 0011)
二、逐个十进制数推导余3码(结合8421码对比)
我们把十进制数 0~9 对应的8421码和余3码列出来,一步一步看推导过程:
| 十进制数 | 8421 BCD码(4位二进制) | 加3(二进制 0011) | 余3码(结果) |
|---|---|---|---|
| 0 | 0000 | 0000 + 0011 = | 0011 |
| 1 | 0001 | 0001 + 0011 = | 0100 |
| 2 | 0010 | 0010 + 0011 = | 0101 |
| 3 | 0011 | 0011 + 0011 = | 0110 |
| 4 | 0100 | 0100 + 0011 = | 0111 |
| 5 | 0101 | 0101 + 0011 = | 1000 |
| 6 | 0110 | 0110 + 0011 = | 1001 |
| 7 | 0111 | 0111 + 0011 = | 1010 |
| 8 | 1000 | 1000 + 0011 = | 1011 |
| 9 | 1001 | 1001 + 0011 = | 1100 |
三、余3码的核心特性(为什么要学它?)
“余3”的含义:
余3码的每个编码都比对应的十进制数大3。例如:- 十进制
0的余3码是0011(0 + 3 = 3,二进制0011); - 十进制
5的余3码是1000(5 + 3 = 8,二进制1000)。
- 十进制
无权码,无固定位权:
余3码没有像8421码那样的“8、4、2、1”位权,不能利用“位权×位值相加”得到十进制数,只能通过“余3码 - 3(二进制0011)”反推十进制数。自反性(对称特性):
余3码中,十进制n和9-n的编码是“反码”关系。例如:- 十进制
0(余3码0011)和9(余3码1100)是反码; - 十进制
1(余3码0100)和8(余3码1011)是反码。
该特性在某些十进制运算(如减法)中可以简化逻辑。
- 十进制
四、快速记忆&验证方法
记住“余3码 = 8421码 + 3”,遇到余3码时,只需将其减去3(二进制0011),就能得到对应的十进制数。
例如:
- 看到余3码
1000,计算1000 - 0011 = 0101(8421码0101对应十进制5),所以该余3码代表十进制5。 - 看到余3码
0110,计算0110 - 0011 = 0011(8421码0011对应十进制3),所以该余3码代表十进制3。
总结
余3码是一种“给8421码加3”得到的无权编码,核心逻辑是**“编码值 = 十进制数 + 3”**。虽然实际应用不如8421码广泛,但它的“余3”规则和自反性很有特点,理解了“加3/减3”的推导,就能轻松掌握啦~
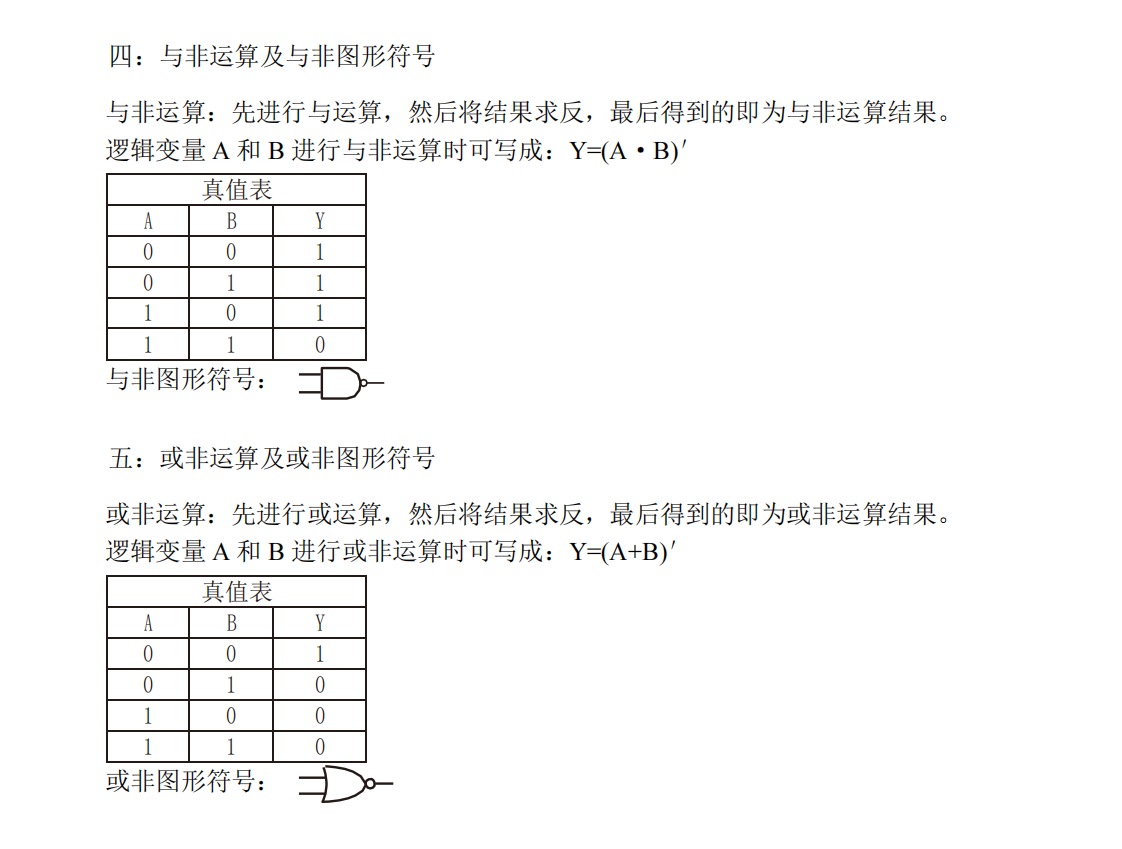
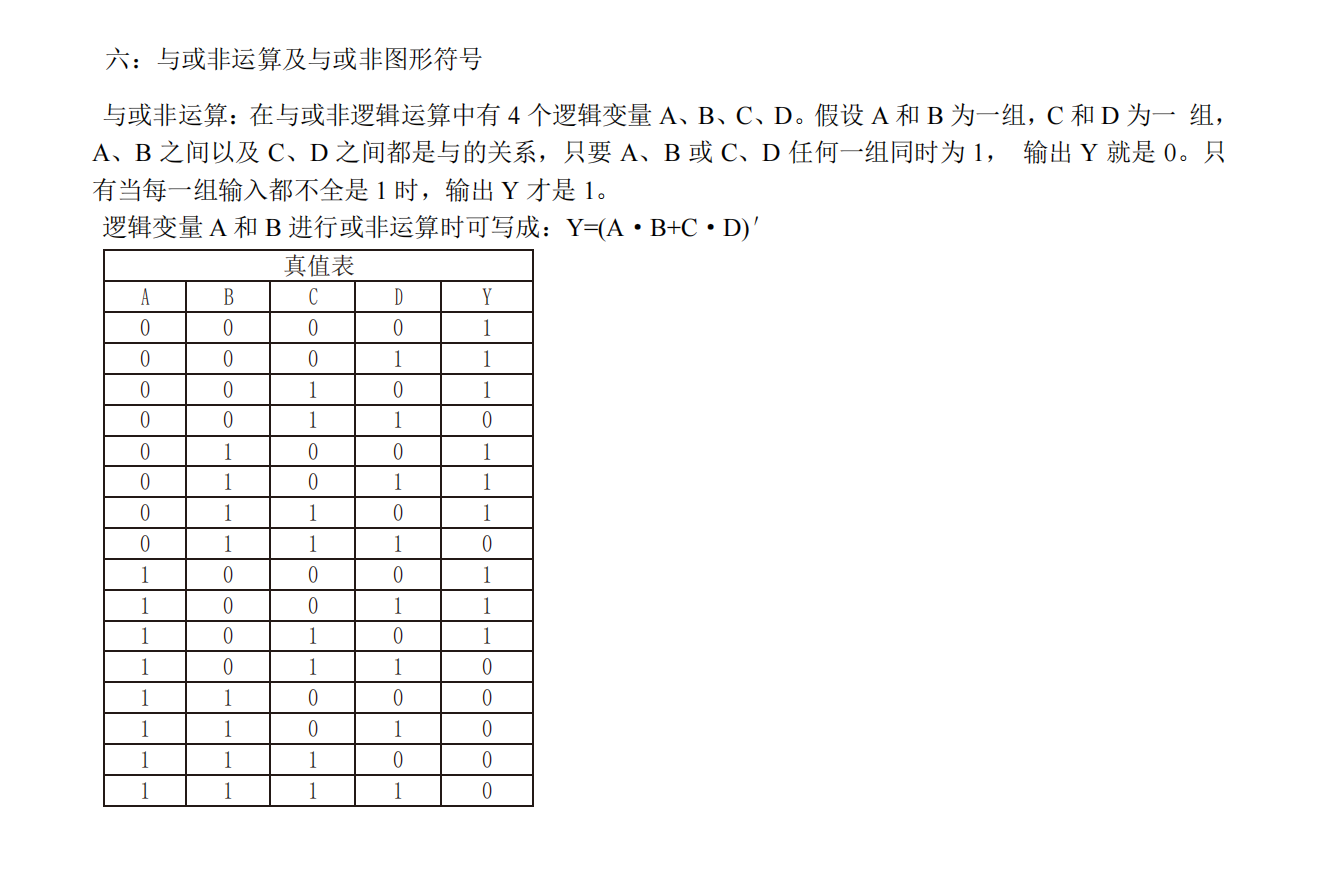
1.5 几种常用的逻辑运算及其图形符号






 浙公网安备 33010602011771号
浙公网安备 33010602011771号