[Nature Machine Intelligence 2025] 基于稀疏学习核的医疗时间序列处理方法：兼顾可解释性与高效性 - 教程

Sparse learned kernels for interpretable
and efficient medical time series processing

https://arxiv.org/pdf/2307.05385

Abstract

对医学时间序列信号进行快速、可靠且准确的解读，对于高风险的临床决策至关重要。深度学习方法在医学信号处理方面提供了前所未有的性能，但代价是：计算密集且缺乏可解释性。本文提出了稀疏混合学习核（Sparse Mixture of Learned Kernels, SMoLK），一种用于医学时间序列处理的可解释架构。SMoLK 学习一组轻量级、灵活的核，形成一个单层稀疏神经网络，不仅提供了可解释性，还具备高效性、鲁棒性以及对未见数据分布的泛化能力。本文还引入了参数削减技术，以在保持性能的同时减小 SMoLK 网络的规模。研究在两项常见于消费级可穿戴设备的重要任务上测试了 SMoLK：光电容积脉搏波（Photoplethysmography, PPG）伪影检测和基于单导联心电图（Electrocardiogram, ECG） 的房颤（Atrial Fibrillation）检测。结果表明，SMoLK 的性能可与参数规模大数个数量级的模型相媲美。它特别适用于启用低功耗设备的实时应用场景，其可解释性在高风险情境中尤具优势。

1. Introduction

在医疗领域中，脑电图（EEG）、心电图（ECG） 和光电容积脉搏波（PPG）等医学信号在患者诊断与监测、及时干预和改善治疗效果方面发挥着核心作用。这些信号通常需要由专业医护人员进行人工判读，然而，随着医疗数据量的爆炸式增长和持续被动监测技术的普及，人工判读效率低下，已成为临床护理流程中的瓶颈环节。

传统信号处理与分类自动化技术虽提升了处理速度，但性能往往受限。深度学习科技的兴起为信号处理带来了革命性突破，其模型性能卓越，但同时也面临着计算成本高和决策过程不透明两大挑战。对于这类"黑盒"模型，常用的事后显著性分析方法往往难以准确识别时间序列中的关键特征。

为兼顾高性能与高可解释性，本文提出了一种创新架构——稀疏混合学习核（Sparse Mixture of Learned Kernels, SMoLK）。该架构经过学得一组轻量级、灵活的卷积核，构建单层稀疏神经网络，在保证优异性能的同时，达成了模型的高效性、鲁棒性和可解释性。值得一提的是，SMoLK的性能可与当前最先进的深度神经网络相媲美，而参数量却减少了数个数量级。

为优化模型效率，本文引入了两种参数削减技术：权重吸收技术将核权重因子融入核本身；相关核剪枝技术则有效消除学习核之间的冗余。

虽然该架构具有广泛适用性，本文重点评估了其在PPG信号分析和单导联ECG分析一种就是中的表现。这两种信号正日益广泛应用于可穿戴设备，适用于长期心脏监测场景。PPG技术通过检测组织中的光吸收变化来测量血容量变化，无创光学检测方法，常用于推断血氧饱和度、心率、心率变异性等心血管参数。随着智能手表等消费级可穿戴设备的普及，从PPG信号中提取有价值信息已成为研究热点。

然而，可穿戴PPG设备存在一个明显缺陷：对运动伪影高度敏感。由于用户日常活动会产生剧烈运动，导致信号失真严重。传统解决方法包括使用加速度计等辅助传感器、基于统计特征的办法、小波去噪算法或手工特征检测器等。这些途径虽能供应清晰的检测依据，但性能通常不及深度神经网络。而深度神经网络又存在参数量大、计算需求高、可解释性差等问题，难以部署在资源受限的可穿戴设备上。

同样地，ECG作为心脏疾病诊断的金标准，在心律失常、心脏病发作等疾病的检测中具有不可替代的价值。尽管已有研究探索采用深度学习模型自动分析ECG信号，但这些方式同样面临着计算效率低和缺乏可解释性的困境。

本文提出的SMoLK方法在PPG信号伪影检测和单导联ECG房颤检测两项任务上均取得了显著成果。在PPG伪影分割任务中，SMoLK实现了三大优势的完美平衡：

1. 达到最先进的性能水平

2. 具有高度可解释性

3. 参数量比当前最优模型少数个数量级

在单导联ECG房颤检测任务中，SMoLK在性能指标上与深度ResNet相当，但参数量不足后者的1%，且在低数据场景下表现尤为出色。

通过在可解释性方面，SMoLK通过学得一组精简的优化卷积核，实现了透明的决策过程。对于PPG信号质量评估，模型通过对信号进行卷积、求和与阈值处理，直接生成质量度量值。这个过程是"近乎线性"的，仅有的非线性操作是将负值置零。这使得本文可以精确量化每个卷积核对最终输出的贡献。对于分类任务，能够通过逆向过程准确计算信号各片段对分类结果的贡献度。值得注意的是，最小规模的SMoLK模型仅运用12个卷积核，研究人员可以直接观察每个学得的特征波形，这与参数量庞大、内部工作机制不透明的深度神经网络形成鲜明对比。

在效率与内存使用方面，SMoLK充分考虑到了实际应用场景的约束。大多数可穿戴设备都是计算能力有限、电池续航紧张的小型设备。SMoLK架构简单，易于进行内存和计算优化，支持16位浮点量化而无明显性能损失。其轻量级特性使得对信号质量或心律失常的实时评估允许作为后台进程运行，仅需几千字节的内存占用。

2. Related Work

2.1 经典统计与机器学习技能

Classical Statistical and Machine Learning Techniques

统计与机器学习方法通过特征提取和分类器构建来检测PPG信号中的运动伪影。早期研究采用基于最小二乘法的X-LMS和自适应滤波器等手艺，也有研究使用峰度和香农熵等统计参数作为检测特征。此外，支持向量机、随机森林和朴素贝叶斯等传统机器学习方法也被广泛应用于此任务。在ECG心律失常检测领域，研究者同样采用了支持向量机、小波变换和逻辑回归等方法。然而，这些方法的性能通常不如深度学习方案，且大多专注于对离散时间块的分类，而非连续的伪影分割任务。

2.2 深度学习方法

Deep Learning Approaches

近年来，一维卷积神经网络、二维卷积神经网络和U-Net类型架构等深度学习手段在PPG伪影检测和ECG心律失常检测中展现出优越性能。虽然这些方法的准确率显著超越传统机器学习，但其原始设计主要针对分类任务，需要通过滑动窗口分类或借助GradCAM、SHAP等解释性设备来适配分割需求，这不仅增加了实现复杂度，其可靠性也受到质疑。基于Transformer的架构虽然取得了与卷积网络相当的精度，但需要更大的参数量。

更关键的是，大多数深度学习模型计算需求庞大，难以部署在资源受限的可穿戴设备上。Tiny-PPG是个例外，它经过模型剪枝建立了紧凑的便携式模型。本文实验表明，在达到相当性能的前提下，本文的手段所需参数量仅为Tiny-PPG的一半。然而，Tiny-PPG仍缺乏模型可解释性。当前研究多采用事后解释方法如GradCAM和SHAP来理解黑盒模型，但这些途径无法提供对模型行为的忠实理解。例如，即使在最新研究中，基于Transformer的医学信号处理模型产生的显著性图谱仍存在特征归因不准的困难，可能忽略关键特征或对无关区域赋予高显著性。

3. Model Architecture

3.1 概述

Overview

本研究将PPG质量分类构建为一个特征检测任务。基本假设是：干净PPG信号具有特定的重复特征，而伪影信号则缺乏这些特征或包含运动引起的异常模式。针对一维时间序列特性，本文设计了一套可学习的卷积核架构来识别这些特征。

具体构建中，本文设置了三种规模的卷积核组（M=12/72/384），并按持续时间分为短（1.0秒）、中（1.5秒）和长（3.0秒）三类，以捕捉不同时间尺度的特征。这些核与输入信号进行卷积运算后，通过max(0,x)函数进行非线性处理，确保输出为非负值。每个卷积通道还引入了可学习的偏置项。最终通过加权求和与Sigmoid函数转换，得到[0.0,1.0]范围内的信号质量评估值。

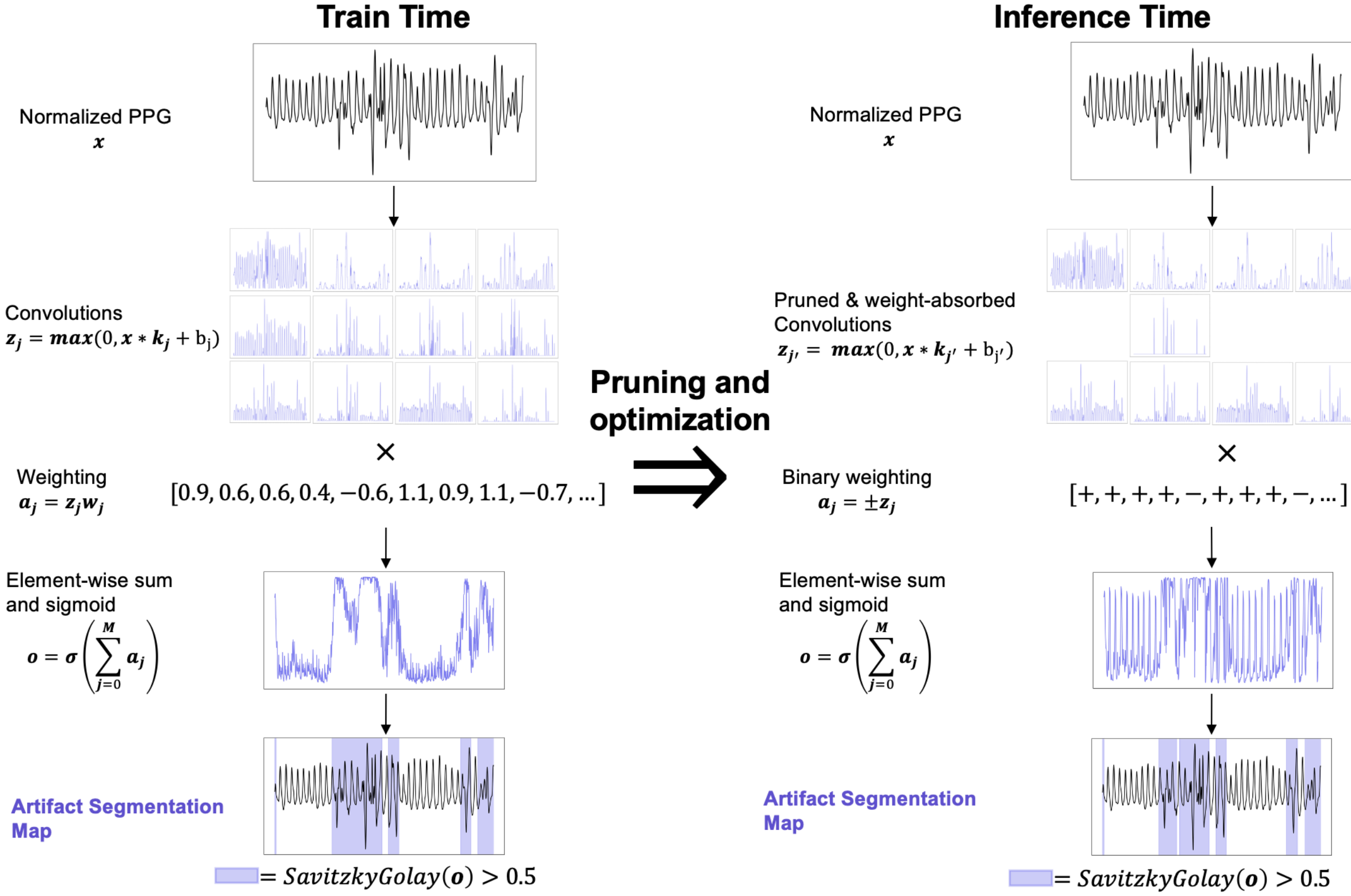
为优化输出质量，本文引入三阶Savitzky-Golay滤波器（0.8秒窗口）进行平滑处理，结果通过阈值处理生成二值分割结果。整个处理流程如图1所示。后处理滤波基于"伪影倾向成群出现"的观察，虽能提升分割平滑度，但对核心评估指标DICE系数影响有限，可根据实际需求作为可选超参数使用（详见附录A）。

图1：PPG处理流程。展示了在训练和推理阶段用于PPG信号质量分割任务的处理流程。第一，对PPG信号进行归一化处理，利用减去均值并除以标准差，使其符合标准正态分布。接着，应用一组卷积核进行卷积运算。本文的最小模型足够轻量，使得所有的卷积后信号都能在此图中显示。卷积后的信号经过上限处理（将负值置零）、加权 和求和 ，然后应用 Sigmoid 函数进行变换。最后，对输出进行平滑和阈值处理，以完成对信号的分割。训练完成后，会利用剪枝相似的核并吸收核权重来减少参数数量。

更形式化地说，该模型由M 个核、M 个标量偏置和 M 个标量权重组成。给定输入信号x，本文的 SMoLK 模型定义如下：

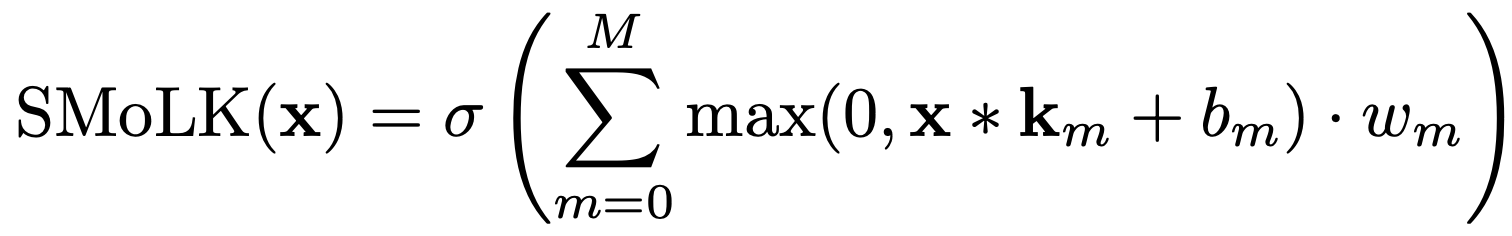
其中，_m、b_m、w_m 分别是第 m个卷积核、偏置和信号权重，符号∗ 表示卷积操作 ，符号 ⋅ 表示标量-向量乘法，σ 是逐元素的 Sigmoid 函数，即 。本质上，SMoLK 等价于将输入与可学习核进行卷积后生成的滤波信号的线性组合，并映射到 (0,1) 范围。对于分割任务，输出可以依据平滑和阈值处理进行进一步后处理，以生成分割图。

3.2 分类

Classification

3.2.1 概述

为展示该架构的通用性，本文对模型的输出稍作修改，以适应分类任务。首先，使用学习到的核生成特征图：

然而，与 PPG 任务中计算特征图的逐元素加权和不同，本文计算每个单独特征图的均值，为每个特征图产生一个分数：

其中，Mean 计算特征图 的逐元素均值。然后，在一个简单的线性模型中应用这些分数来产生一个逻辑值：

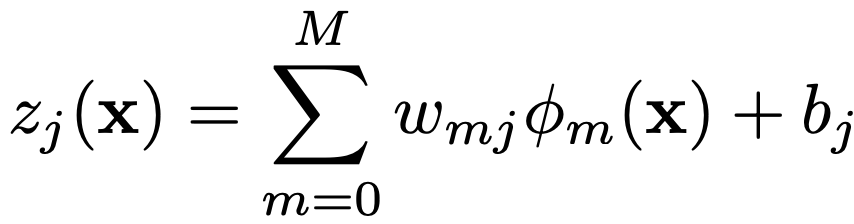
其中，w_{mj} 是第 m个特征对于第j个类别的权重，b_j是该类别的偏置。在 ECG 分类的情况下，本文通过计算 ECG 信号的功率谱并将其作为线性分量加入，从而在线性模型中添加了全局频率信息：

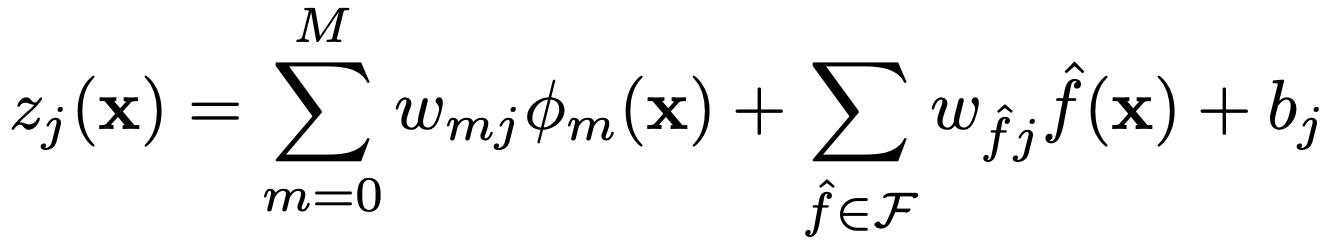
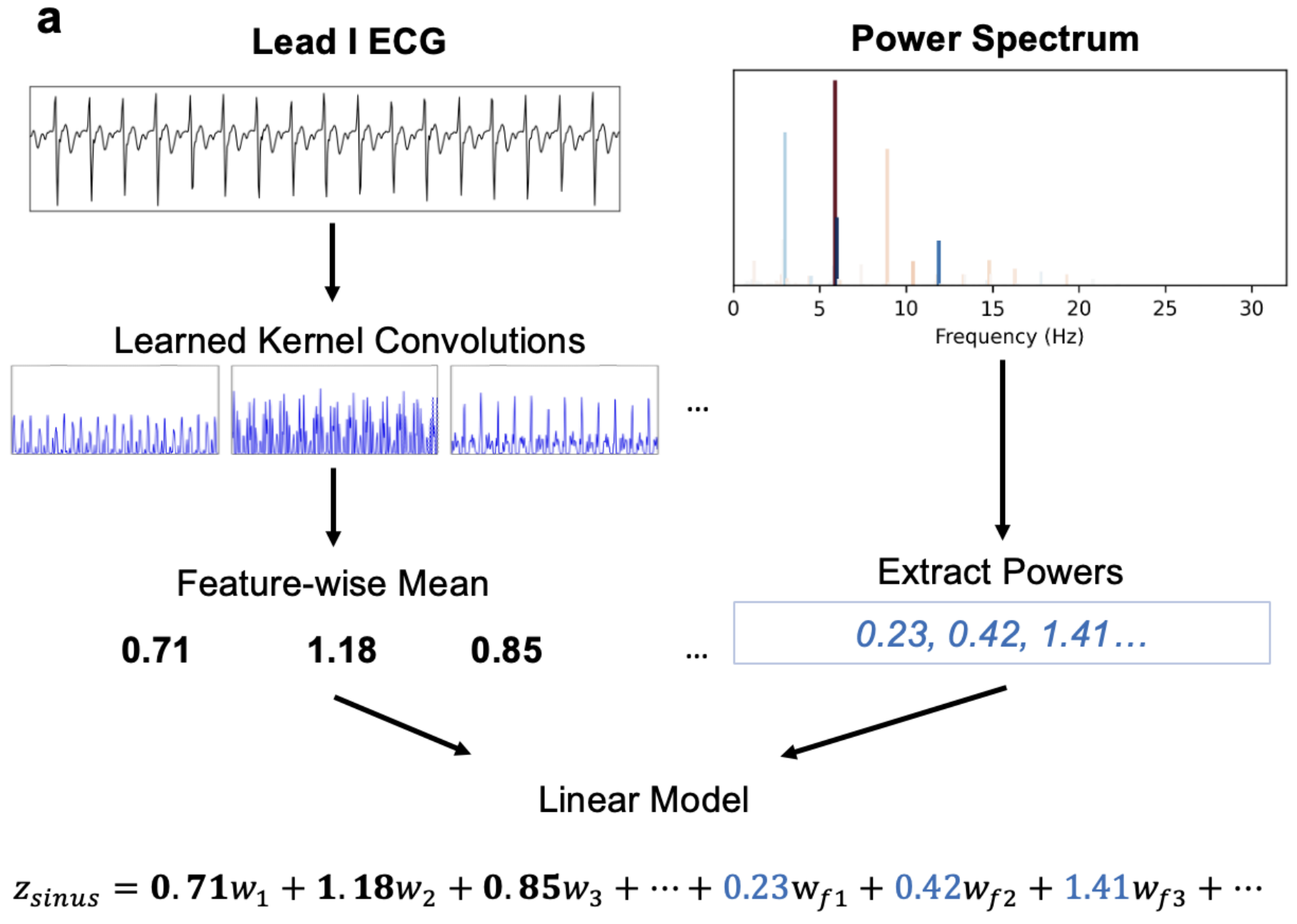
其中，f^() 是功率谱 ℱ 中信号 的频带，w_{f^j}是该频带对于类别j的相应权重。最后，可以对此逻辑值应用非线性激活函数以生成概率分布。本文使用SoftMax函数，其定义为，其中 z_j 是类别 j的逻辑值。该流程的图示概览见图 2a。

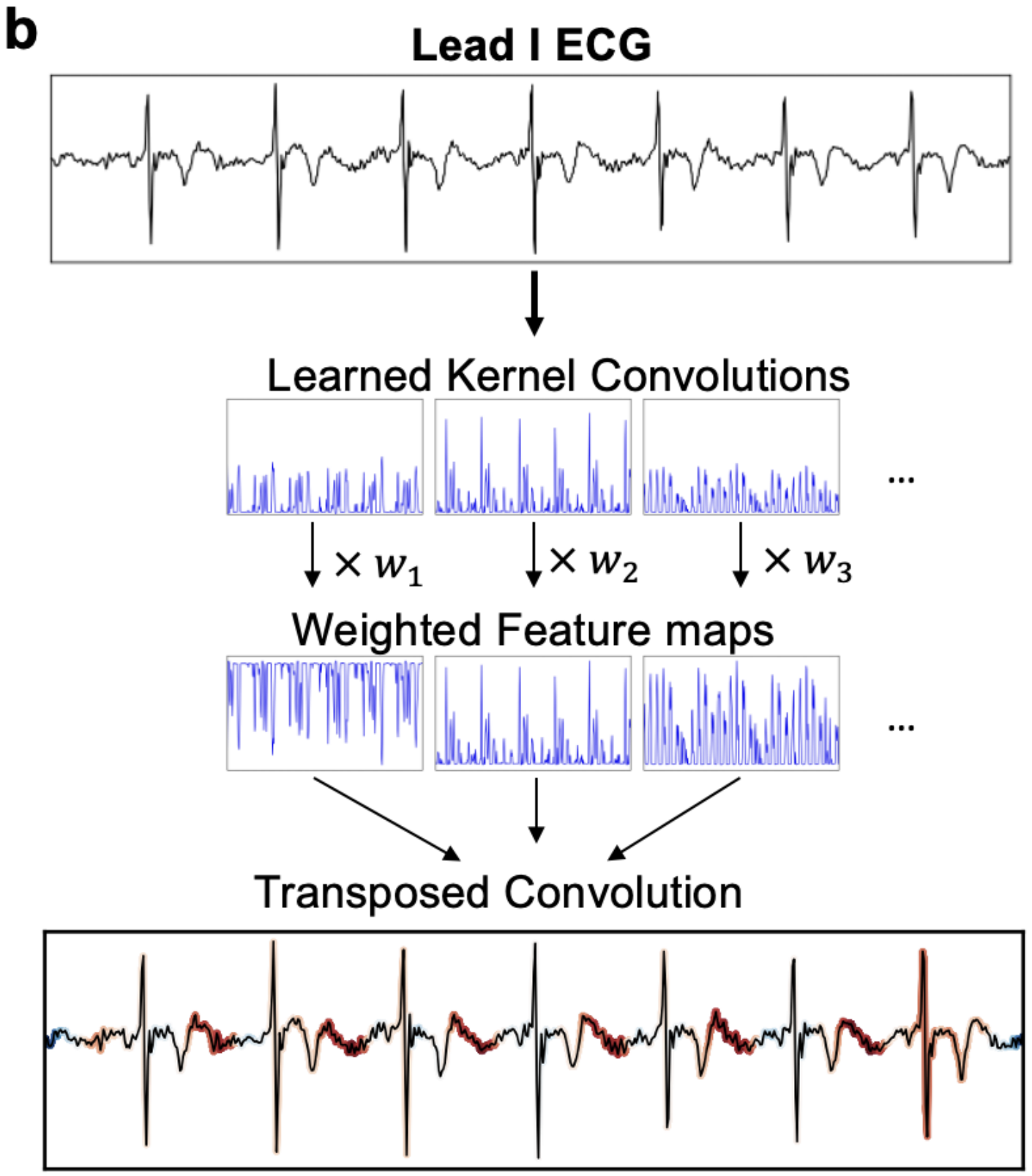
图2：ECG处理流程。a.处理单导联 ECG 的流程。首先，将一组学习到的卷积核应用于 ECG 信号，生成若干特征图。接着，计算每个特征图的均值，这些均值被用作线性模型的输入。从功率谱中获得的全局频率信息也作为线性模型的输入，以产生一个逻辑值。

3.2.2 可解释性

由于该模型是特征图均值激活的线性组合，并且每个激活都是由信号上的卷积执行生成的，因此本文可以借助反转卷积来直接计算输入信号的每个部分对给定输出类别的贡献。如算法1 所述，本文按下述方式计算贡献图。概括地说，首先照常执行前向传播并计算特征图的值。然后，将这些特征图与所关注类别的特征权重进行逐元素相乘。最后，将此乘积结果通过反向卷积处理存入一个与输入 ECG 信号维度相同的贡献图缓冲区中。这使得本文能够精确计算输入信号的任何给定部分对输出分类的贡献程度。该过程的图示可见图 2b。

算法1 的概要描述：该算法通过利用前向传播中计算得到的特征图和线性分类层的权重w_{mj}，执行一个反向传播过程。具体步骤包括初始化一个与输入信号等长的零向量作为贡献图，然后对于每个特征核m 和每个类别 j，将特征图 与对应的权重w_{mj}相乘，再通过转置卷积核_m将加权后的特征图"映射回"输入信号空间，并将其累加到贡献图中。最终得到的贡献图清晰地表现了输入信号中每个时间点对最终分类决策的重要性程度。

图2：ECG处理流程。b.用于解释子图a中从学习核模型得到的预测的反向流程。首先，以与a相同的方式，通过学习的卷积核生成特征图。然而，这里并非计算特征图的均值，而是将特征图与其对应的类别权重进行逐元素相乘。功率谱不用于解释过程。最后，应用转置卷积来计算输入信号每个部分的重要性。该方法几乎是前向过程的精确逆过程，允许以原则性的方式将重要性分配给与输出类别逻辑值直接相关的输入信号。值得注意的是，该方法正确地将延长的 PR 间期标记为将此 ECG 分类为一度心脏传导阻滞的最重点特征，表明本文的模型学习到了重要特征而非伪相关。

3.3 权重吸收

Weight Absorption

通过得益于模型的"近乎线性"特性，本文能够通过将权重因子吸收到核自身内部来减少分割模型的参数数量。令为输入的 PPG 信号，它是一个长度为 1920 的向量。令_m、b_m、w_m 分别是第 m个卷积核、偏置和信号权重。这些核是根据长度类别（长、中、短）分别为长度 192、96 或 64 的向量，而偏置和权重是标量。推导过程如下：

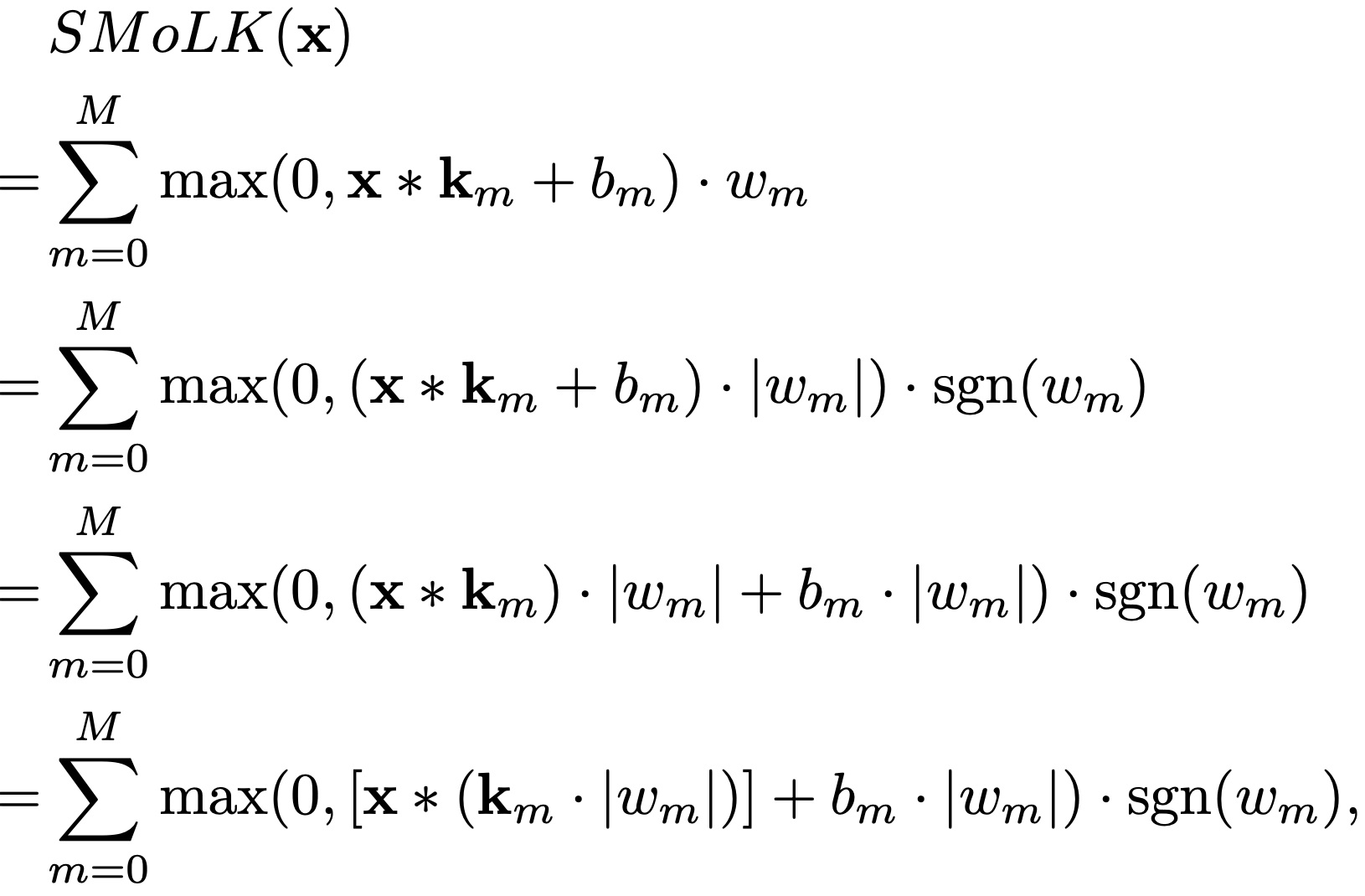
其中，|⋅|表示逐元素的绝对值，sgn 表示符号函数。

此时，量 _m ⋅ |w_m|成为了新的核，量b_m ⋅ |w_m|成为了新的偏置。因此，本文可以减少参数数量，因为现在可以存储核本身以及一个对应的二进制值（指示它们是正核还是负核）。此外，每个核可以被清晰地归类为"有助于良好信号质量"（正核）或"有助于不良信号质量"（负核）。这个过程在核学习完成后执行，旨在减少已部署模型的内存占用和标量运算次数。

3.4 相关核剪枝

Correlated Kernel Pruning

受到一些学习到的核看起来很相似的观察所驱动，本文假设可能在保持良好性能的同时剪枝 相似的核。为了度量核之间的相似性，本文使用欧几里得距离。

概括地说，本文的核剪枝方法包括以下步骤：

1. 计算所有核之间的成对相似性。

2. 识别出高度相似的核对。

3. 移除冗余的核，并调整剩余核的权重以补偿被移除核的贡献。

关于剪枝过程的严格描述将在方法部分讨论。

4. Method

本研究采用 PyTorch 2.1.1 和 Scikit-learn 1.3.2 进行机器学习任务，借助 SciPy 1.9.3 和 NumPy 1.22.4 完成数据分析和统计计算。

4.1 内容集与预处理

Datasets and Preprocessing

模型训练基于PPG-DaLiA数据集，并在该数据集的测试集以及WESAD 和 TROIKA资料集上进行性能评估。PPG-DaLiA 包括15名受试者在日常活动（如静坐、步行、运动驾驶）中采集的心电图、加速度计和皮肤电活动信号。WESAD 数据集聚焦情绪状态监测，采集了15名受试者的手腕与胸部PPG信号。TROIKA 则记录了12名受试者在跑步机运动时的多模态信号，因其高强度运动场景导致的信号质量挑战，成为泛化性评估最具挑战性的数据集。

预处理流程采用与先前研究相同的带通滤波器设置（0.9-5 Hz），将数据分割为30秒片段并重采样至64 Hz。与将资料归一化至[0,1]区间不同，本文采用数据块级别的单位正态分布归一化，以增强模型对信号强度变化的适应性。伪影分割标签直接采用公开的专家标注结果。

在ECG实验中，重点评估单导联房颤检测任务。训练使用Computing in Cardiology 数据集，包含窦性心律、房颤和"其他"心律失常三类有效记录。尽管模型支持可变长度输入，为便于比较，统一分割为10秒片段，最终获得16742个窦性样本、2463个房颤样本和8685个"其他"样本。预处理采用1.0-10.0 Hz带通滤波和逐样本的单位正态归一化。

泛化能力测试使用来自查普曼大学合作医院的独立数据集，该12导联ECG数据集中，本文仅采用I导联数据进行单导联任务分析，预处理流程与训练集保持一致。

4.2 PPG信号分割

PPG Segmentation

本研究经过系统实验对比提出的手段与多种基线模型，包括基于U-Net的先进架构。结果显示，本文的分割算法在多个PPG基准任务中达到或超越了最优性能。

4.2.1 训练配置

模型训练采用Adam优化器（β₁=0.9, β₂=0.999, ε=10⁻⁸, 权重衰减=10⁻⁴）结合线性学习率衰减策略（0.01→0.002），以二值交叉熵误差作为损失函数。由于模型参数量（10³-10⁵）远小于数据集规模（10⁸），采用全数据集梯度计算以确保训练稳定性。针对大规模模型，使用梯度累积技术克服内存限制。经过512轮全数据集迭代训练发现，该方法相比随机小批量训练具有更优的经验性能，且在不同参数规模下均未观察到过拟合现象。

4.2.2 剪枝

为确定需要剪枝的卷积核，本文计算了卷积核的"有效贡献"，定义如下：

其中，w_j 和 w_k是一对卷积核中两个核的权重，μ_j 和 μ_k卷积核就是分别w_j 和 w_k 的平均绝对值。本文保留奏效贡献较高的卷积核，并剪除另一个卷积核。

在剪除一个卷积核时，需更新剩余卷积核的权重和偏置，以校正被移除卷积核的贡献。不失一般性地，假设eff_j > eff_k。剩余卷积核j的权重和偏置更新方式如下：

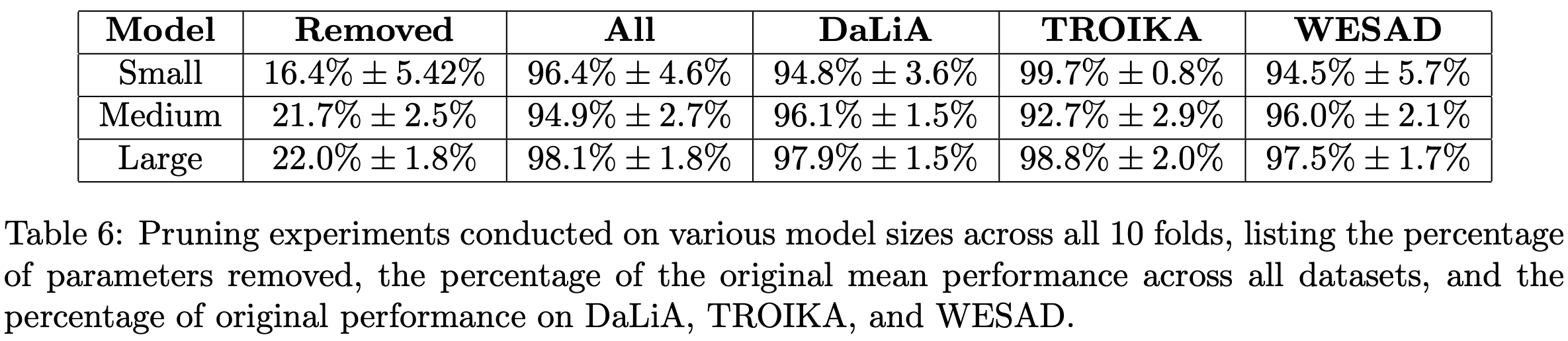
其中，b_j 和 b_k 分别是权重 w_j 和 w_k对应的偏置。本质上，两个卷积核的偏置被简单合并为一项以补偿剪枝操作，同时剩余卷积核的权重按比例增加，以弥补被剪枝卷积核的信号损失。该技术使得本文最大模型的参数数量能够减少22%，而在所有数据集上的性能绝对下降幅度小于2%（参见附录中的表7）。此外，该工艺具有适应性，允许以更高的性能代价移除更多参数，或以更小的性能代价移除较少的参数。值得注意的是，欧几里得距离的选择是任意的，在剪枝步骤中可以选择任何距离度量。实际上，运用多种不同的距离度量都能得到相似的结果。

本文在三种不同模型规模下提供了示例性的剪枝结果，其目标性能下降不超过 5%（参见附录中的表6）。需要说明的是，研究者可以通过本文的开源 GitHub 代码库来实验这一剪枝过程。

此外，本文展示了启用不同距离度量的剪枝结果表现相对一致，表明该办法对所选距离度量具有鲁棒性。本文在大型模型上测试了另外三种距离度量：功率谱间的余弦相似度（频域中的余弦距离）、特征空间中的余弦相似度（特征向量本身的余弦相似度）和曼哈顿距离（参见附录中的表7）。

4.2.3 评估

为评估基线模型和学习卷积核在伪影检测上的性能，本文采用了DICE 系数，其定义为：

其中，A 和 B分别是预测值和真实值的二值分割图，|⋅| 表示集合的基数（即元素个数）。该指标在 PPG 信号的测试集上进行计算，每个 30 秒的 PPG 信号块均按前述方法进行了归一化处理。本文使用了 10 个不同随机种子训练的模型，进行了10 折交叉验证。

4.2.4 基线模型

本文与 Guo 等人测试的相同基线模型进行了比较。主要包括：卷积神经网络滑动窗口方法、模板匹配方法，以及基于 ResNet-34 并结合 GradCAM或 SHAP进行分割的分类器。更多细节见基线方法部分。

4.3 房颤检测

Atrial Fibrillation Detection

4.3.1 训练

本文以类似方式训练了基于学习卷积核的房颤检测器，使用AdamW 优化器（参数设置为 β₁=0.9, β₂=0.999, ε=10⁻⁸, 权重衰减=10⁻²），并结合线性学习率衰减策略（学习率从 0.1 衰减至最终迭代时的 0.0），共训练 512 个周期，损失函数为多分类交叉熵误差。然而，由于内存限制，训练时的批量大小设为 1024，而非在整个数据集上进行。

4.3.2 评估

本文计算 F1 分数和 AUC-ROC曲线下面积作为主要评估指标。模型在 Computing in Cardiology 数据集上训练，并以 10 折交叉验证的 F1 分数作为优化目标。随后，在由前述 Zheng 等人数据集 构建的、完全独立的测试集上测试模型的泛化性能。

4.3.3 基线模型

本文与医学信号处理中常见的深度学习架构（即1D-ResNet）以及几个先前最优的低参数量卷积神经网络进行了比较。这些基线模型的概述见基线方法部分。

4.3.4 可解释性

为展示技巧的可解释性，本文额外训练了一个学习卷积核分类器，用于区分一度房室传导阻滞 [1º Atrioventricular Block]（1140 个样本）和窦性心律 [Sinus Rhythm]因为其由单一显著特征（即就是（8125 个样本）。选择一度房室传导阻滞PR 间期延长）定义，而非一组全局特征（如房颤中不规则的、无规律的心搏）。该数据同样采集自 Zheng 等人的资料集。

4.4 基线方法

Baseline Methods

4.4.1 卷积滑动窗口

该基线模型采用一维卷积网络结构，用于对3秒窗口的PPG信号进行"伪影/干净"二分类。网络具备3个卷积-ReLU-批归一化-最大池化模块，卷积核尺寸分别为10/5/3，通道数配置为64/64/128。利用从训练集中随机采样的5000个3秒窗口进行200轮训练，优化目标为最小化交叉熵损失。推理阶段采用步长为1秒的滑动窗口策略，当某个1秒片段对应的3个分类输出中出现任一伪影判定时，即将该片段标记为伪影。

4.4.2 模板匹配

该手段基于动态时间规整技能进行模板匹配。首先从训练集中提取10个洁净脉搏波作为标准模板，计算测试脉搏波与所有模板的最小DTW距离。通过网格搜索确定最优距离阈值为1，当最小DTW距离超过该阈值时，判定整个脉搏波为伪影段。

4.4.3 GradCAM与SHAP

本研究复现了基于ResNet-34架构的迁移学习方案。启用在重症监护素材集上预训练的模型，对最终两个残差块及分类层进行微调。训练采用渐进式下降的学习率策略（10⁻⁵→10⁻⁶），共训练100个周期。为将分类模型转换为分割模型，采用两种事后可解释性途径：

• GradCAM：通过反向传播梯度生成特征重要性热力图

• SHAP：基于博弈论计算每个时间点的沙普利值
  通过对显著性图谱进行高斯平滑和阈值处理，生成最终的分割掩码。

4.4.4 Segade

该对比模型是基于U-Net架构的专用分割网络，采用残差卷积模块增强梯度传播，针对一维信号特性进行架构优化，具体构建细节参见原论文。

4.4.5 Tiny-PPG

作为当前最优的轻量级模型，该网络集成深度可分离卷积与空洞空间金字塔池化模块，采用联合监督-对比损失进行训练。本文通过其开源代码复现实验，在保持原训练设置不变的情况下，扩展其在WESAD和TROIKA数据集的基准测试结果。

4.4.6 ResNet-1D

本文适配了开源的心律失常分类模型，将输入通道数调整为1以适应单导联任务，同步调整卷积步长与核尺寸保持特征图维度一致性。模型训练采用512周期标准流程，使用AdamW优化器配合线性学习率衰减策略。

4.4.7 Jia-CNN

本文沿用原有三种卷积架构，为适配三分类任务将输出层维度调整为3。针对250Hz输入要求调整重采样频率，其余预处理流程保持一致。训练中对Jia-CNN1/3采用0.005的学习率，Jia-CNN2采用0.002的学习率以确保模型收敛稳定性。

5. Results

5.1 PPG信号分割

PPG Segmentation

5.1.1 测试集性能

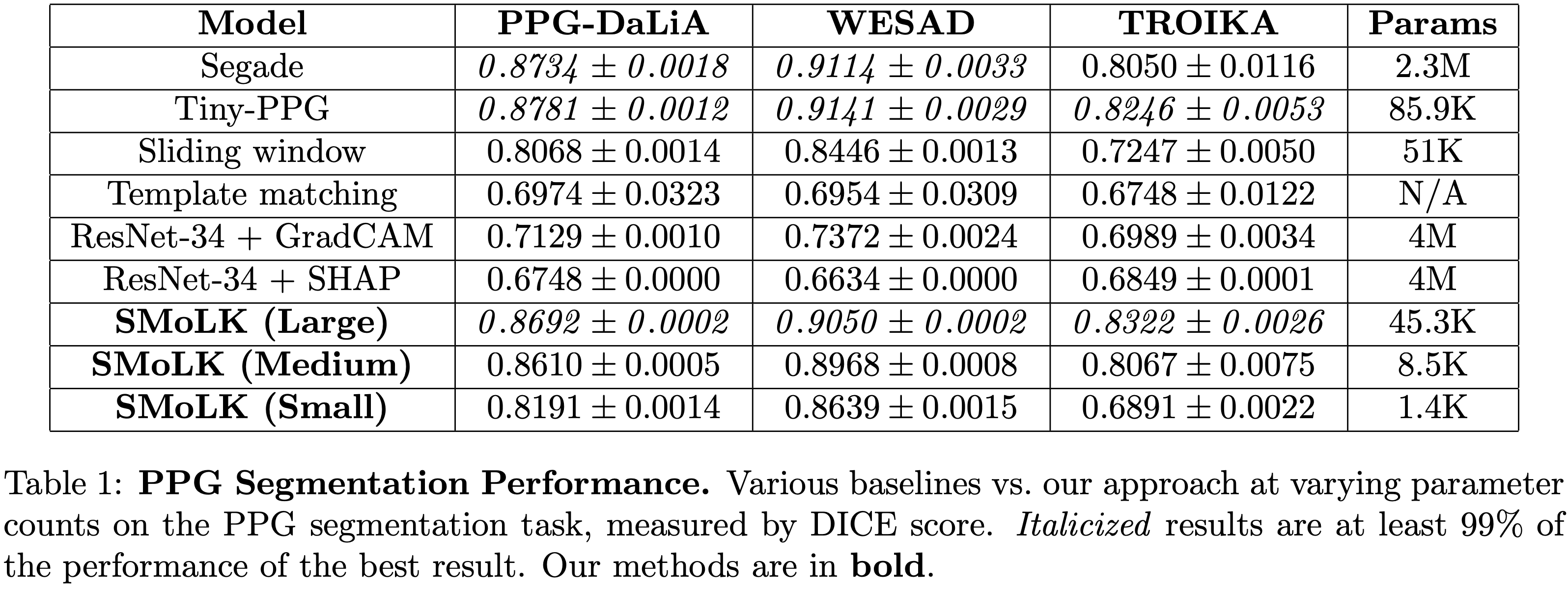
通过在DaLiA、WESAD和TROIKA三个数据集上的系统测试，本研究提出的方法在PPG信号分割任务中展现出卓越性能。与当前最优的Segade和Tiny-PPG模型相比，本文的最大模型在DaLiA和WESAD数据集上实现了超过99%的相对DICE系数，而参数数量分别仅为Segade的不到2%和Tiny-PPG的一半。即使在最具挑战性的TROIKA数据集上，该模型也显著优于其他基线方法。

模型的可扩展性表现同样令人满意：中等模型以仅0.4%的参数规模，在所有数据集上达到Segade模型98%以上的性能；最小模型以0.06%的参数量，在DaLiA和WESAD数据集上保持94%的性能水平，在TROIKA数据集上仍能达到86%的基准性能。详细性能对比参见表1。

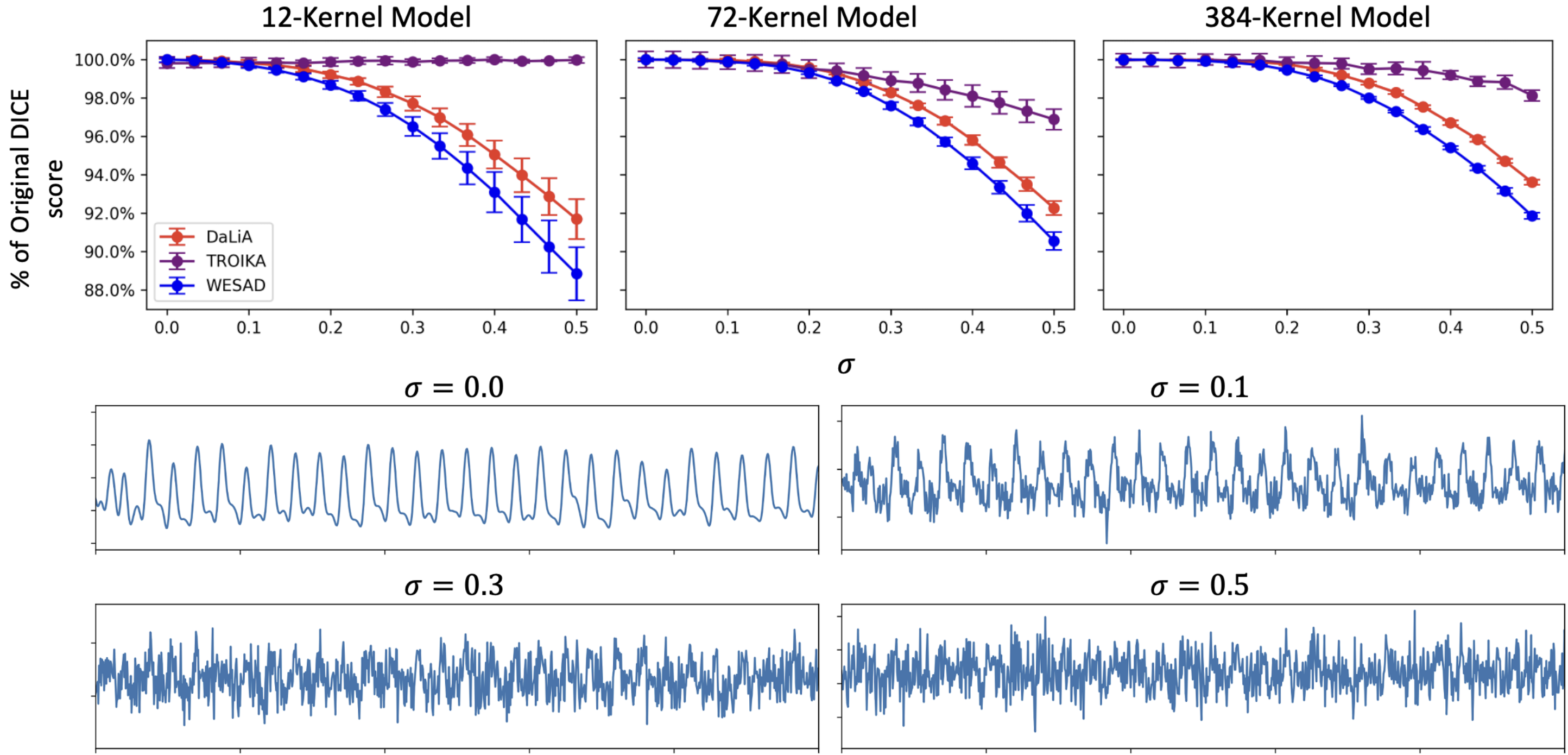
此外，模型展现出优秀的噪声鲁棒性，在未经过高斯噪声增强训练的情况下，测试时添加不同强度噪声仅引起DICE系数的轻微下降（附录图9）。实验还表明，即使在参数量较大的情况下，模型也表现出良好的抗过拟合特性，性能上限可能主要受限于数据标注精度（附录B和C）。

Figure 9:The performance of the learned kernel model as compared to baseline performance on the clean test signal (above panels). Examples of a PPG signals with various amounts of Gaussian noise added (bottom panels).

5.1.2 可解释性

本研究手段的突出优势在于其内在可解释性。基于单层卷积核的简洁架构，使得我们可能直接分析每个卷积核对最终输出的贡献程度。

通过定义的核重要性度量公式：

其中， 表示第 m个核各分量平方和，b_m是该核的偏置，w_m是该核的权重。根据定义，该公式计算的是当该核与一个完全匹配的模板完美重合时，它向最终信号增加的值。此外，本文还指出，在核和偏置已归一化（即）的情况下，核重要性直接等于该核的权重。本文对小、中、大三种模型规模的所有 10 个交叉验证模型均进行了此项核分析。

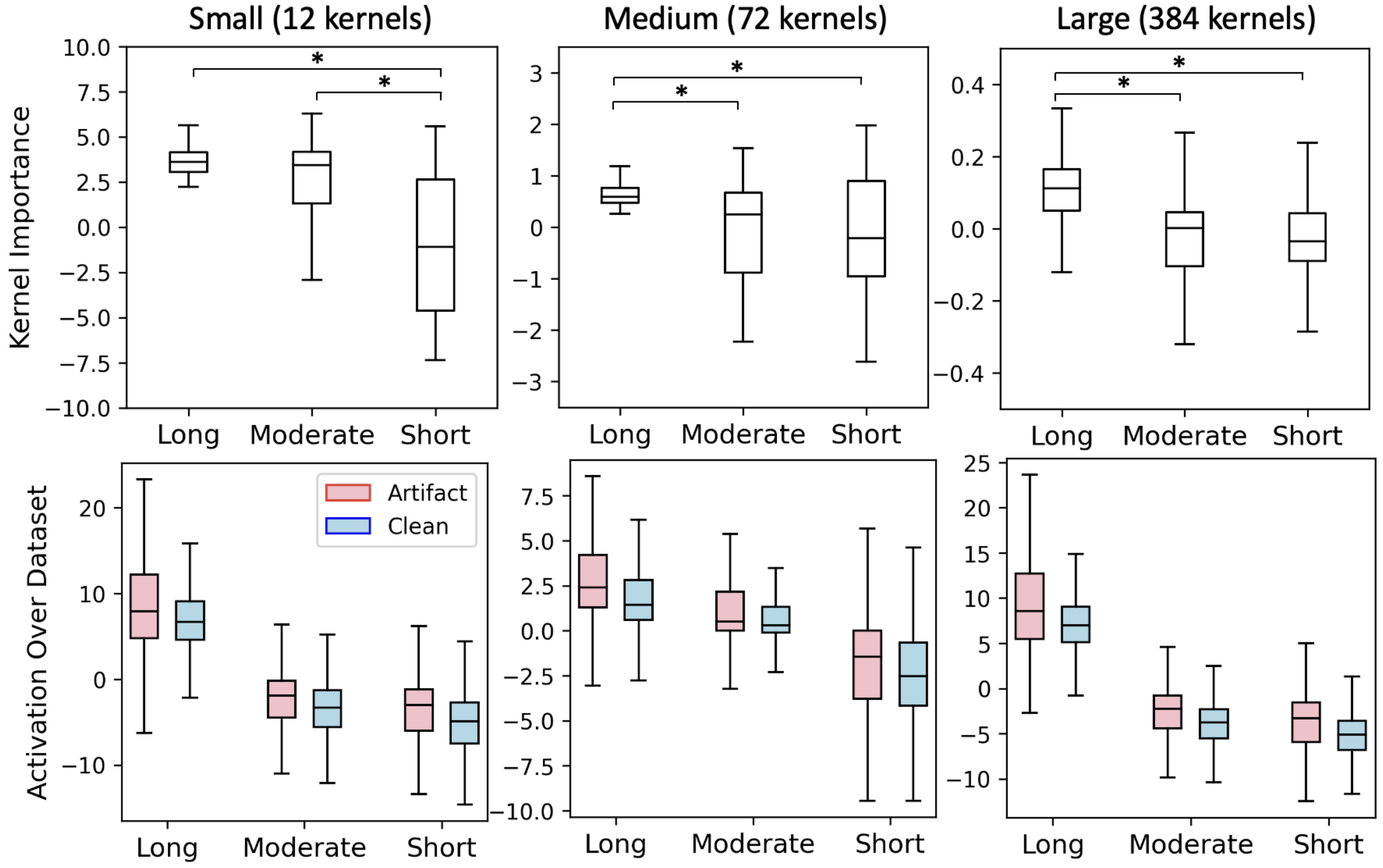
本文注意到卷积核大小与其重要性之间存在明显的规律。研究发现，对于中型和大型模型，长核的平均重要性显著高于短核和中长核（p < 10⁻¹³，显著性通过双尾独立样本 t 检验计算）。对于小型模型，长核和中长核的平均重要性显著高于短核（p < 10⁻⁶）（参见图3）。这些结果表明，长核通常学会识别低质量的信号特征，而中长核和短核则学会识别干净的 PPG 特征。

图3：核统计信息。（上图）各模型规模中每种核计算得到的"核重要性"。（下图）在数据集的干净片段和伪影片段上观察到的各核组的经验平均激活值。计算得到的"核重要性"的显著差异反映在了这些核组在测试集上的经验输出值中。显著性通过经过 Bonferroni 校正的双尾独立样本 t 检验计算。由于样本量极大，经验核输出之间的所有差异均具有统计显著性。所有箱线图均以中位数作为中心线，四分位距作为箱体，须线表示分布的最小值和最大值。离群点定义为超出±1.5 × IQR范围的点，为清晰起见未在图中显示，但所有点均包含在统计分析中。

干净信号生成来进行分组，从而对上述论断进行了实证研究。本质上，本文按大小（长、中、短）对卷积核进行分组，在整个测试数据集上执行卷积和加权操作，并将输出值合并为一个数组。进一步地，根据生成这些输出值的 PPG 信号被标记为"伪影"或"干净"来进行划分。在该模型的框架下，这等价于计算：就是本文通过计算每个核大小组在整个测试数据集上的激活值，并根据这些激活值是由包含伪影的 PPG 信号还

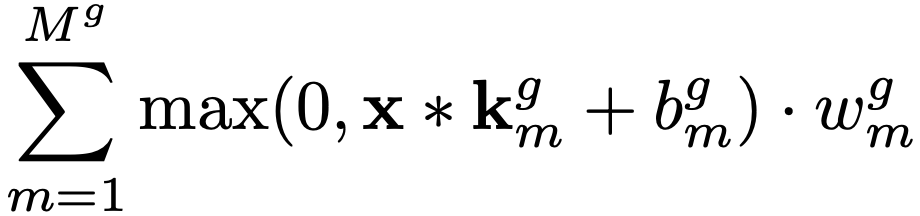
其中，g代表所讨论的核组（即长、中、短核），M_g 是组 g中的核数量，^g 是组 g的偏置向量，^g 是与核组 g相关的权重向量。

研究发现，对核重要性的数学分析所得出的论断与实证结果一致：长核大部分时间产生正值，中长核主要产生负值或正负混合值（如中型模型中所示），而短核主要产生负值，如图3所示。图4展示了一个30秒长的具体示例。对核重要性的数学探索与不同核组在测试集上产生的输出值的实证探索之间的一致性表明，无需依赖事后解释方法，即可对模型行为得出有意义的结论。这些结果通过比较图3的上下两行得以展示。

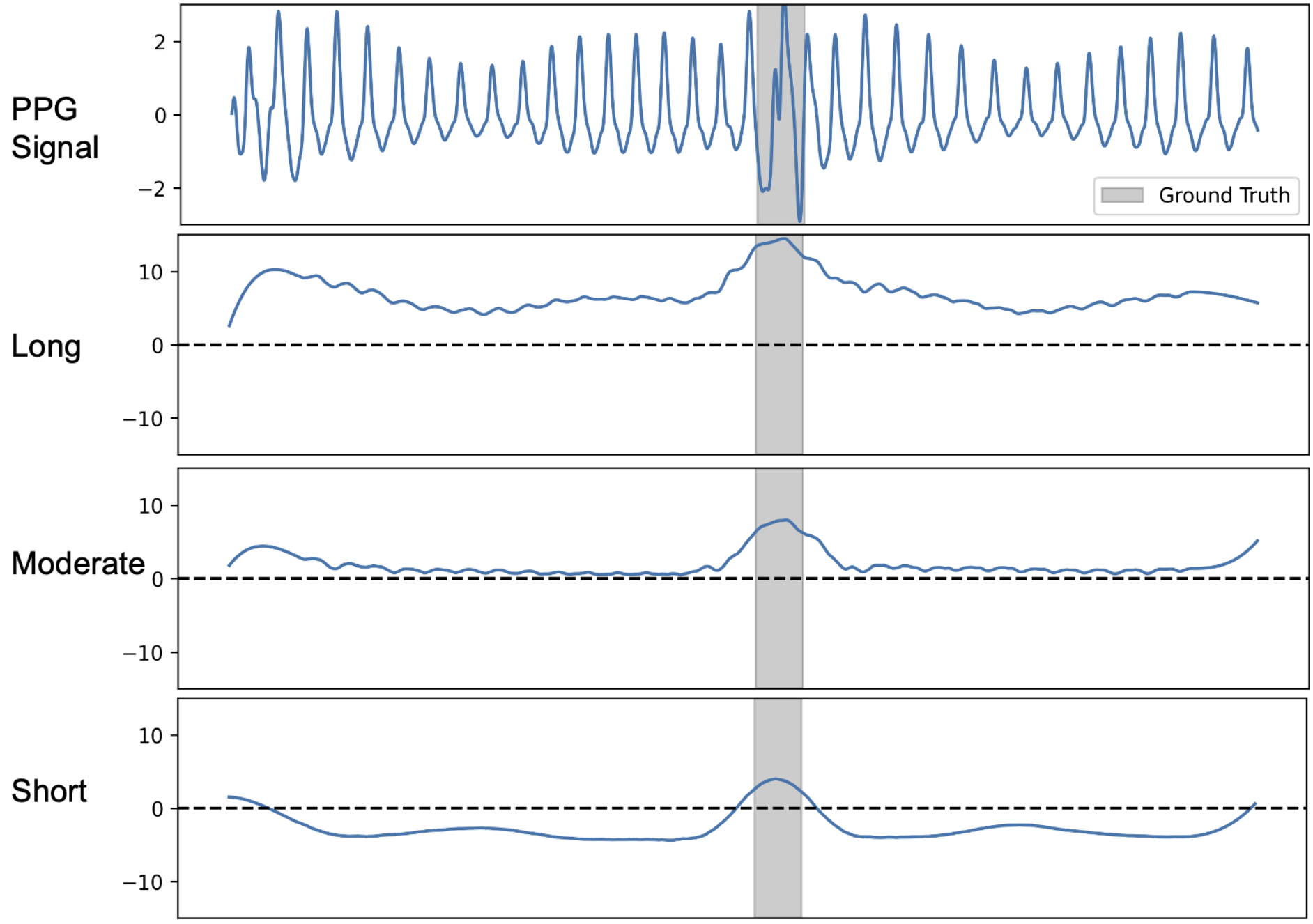
图4：PPG分割示例。一个30秒PPG信号的处理过程示例，展示了不同长度卷积核组的贡献。从上至下分别为：a) 输入PPG信号（灰色）与真实分割标签（绿色：干净，红色：伪影）；b) 短核组的加权输出；c) 中长核组的加权输出；d) 长核组的加权输出；e) 所有核组合并后的模型总输出（Sigmoid函数之前）；f) 最终预测概率（Sigmoid函数之后）与经过后处理（平滑和阈值处理）的二进制分割输出（黑色）。许可看出，长核组（d）在伪影区域贡献了强烈的正向信号，而中长核和短核组（b, c）在干净区域贡献了负向信号，共同决定了最终的分割结果。

图4解读：各核组对总输出信号的贡献。能够明显观察到，"长"核即使在干净信号段进行卷积时也产生正信号；"中长"核在干净信号段卷积时信号接近零，在伪影段则产生正值；而"短"核除在伪影段外，通常产生负值。

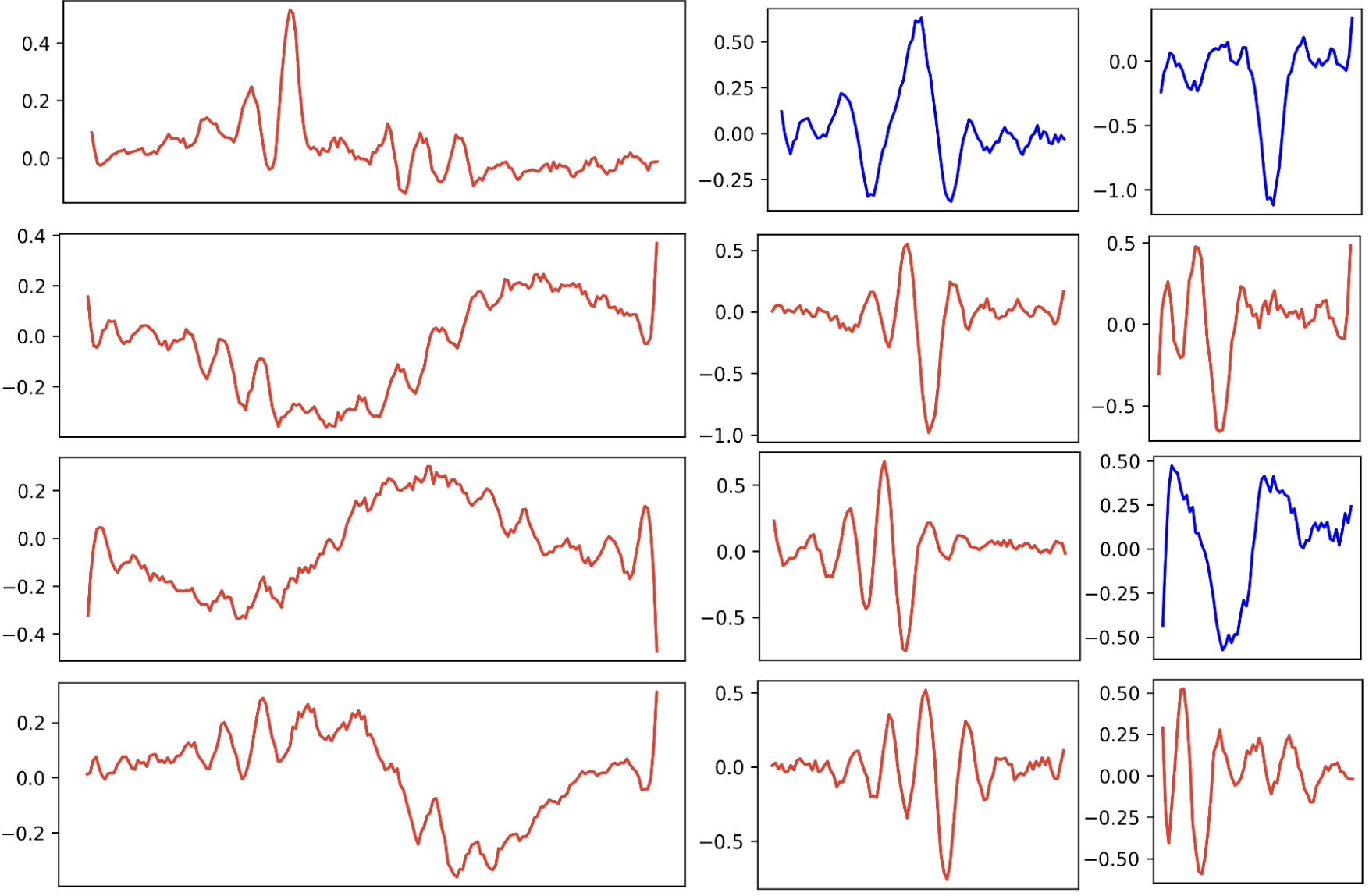
，就是特有值得注意的最小模型仅包含12个可视化卷积核（附录图8），这种极简的参数量使得人工检查每个学习到的特征模式成为可能，与传统深度学习模型的"黑盒"特性形成鲜明对比。

Figure 8:All 12 kernels of the small model. Blue kernels contribute primarily to the detection of “clean” signals and red kernels contribute primarily to the detection of artifacts.

5.1.3 剪枝实验

剪枝实验表明，针对长核的剪枝策略能够建立最佳的压缩效率，在性能损失最小的情况下实现最大的参数量削减。随着模型初始规模的增加，可移除的参数比例相应提升，同时性能下降更加平缓，这反映了大模型内部存在更高的参数冗余度。

本文在附录表6中提供了具体的剪枝方案，这些方案能够在保持96%原始性能的前提下显著减小模型尺寸。此外，得益于模型的近乎线性结构，权重量化过程异常简便，从float32到float16的转换几乎不引起性能损失，这与深度神经网络复杂的量化流程形成鲜明对比。

5.2 房颤检测

Atrial Fibrillation Detection

5.2.1 分类性能

本文将提出的12核、72核 和 384核 模型与一个 16层 ResNet以及一个先前最优的卷积神经网络进行了比较。模型在Computing in Cardiology 房颤检测数据集上进行训练和验证，并在独立保留测试集 [Holdout Set]上进行测试（训练/测试方法及材料集描述见方法部分）。

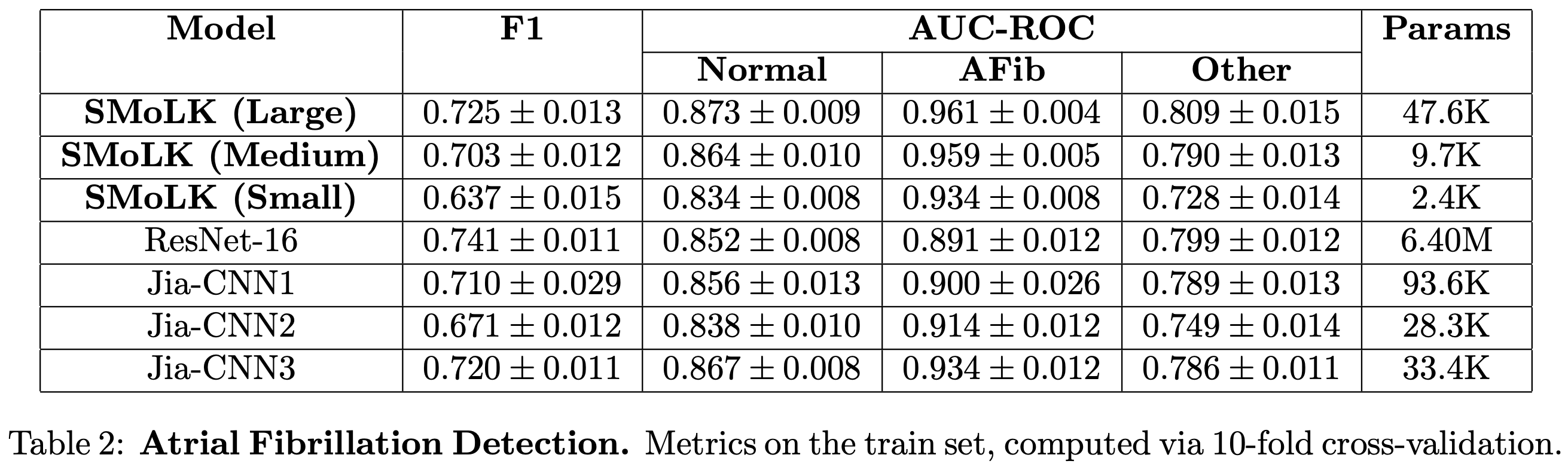
在 10折交叉验证集 上，中型和大型 SMoLK 模型在 AUC-ROC（一项关键临床指标）上达到或超越了所有其他基线模型的性能（见表2），尽管其参数数量显著更少（不足 ResNet-16 参数量的 1%）。

在独立保留测试集上，所有 SMoLK 模型在正常心律和房颤检测上的 AUC-ROC 均优于其他基线模型（见表3）。然而，在检测未知的"其他"心律方面，其性能逊于本文测试的两个参数量最高的模型：16层 ResNet（称为ResNet-16）和一个先前最优的卷积神经网络（称为Jia-CNN1）。

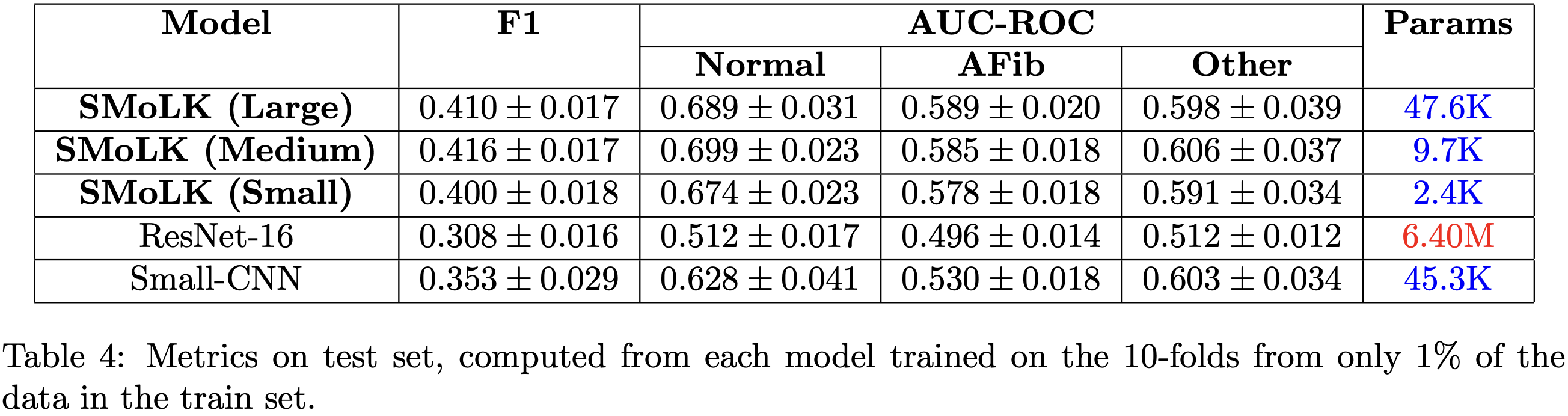
本文还发现，所提出的模型在低数据量情况下表现出更好的训练和泛化能力。当仅使用 1% 的数据集进行训练时，本文方法在训练集和保留测试集上的F1 分数 和 AUC-ROC均高于所有基线模型，而 ResNet-16 的性能则与随机猜测相当。本文推测这可能是由于 ResNet-16 模型的过参数化 [Overparameterization]所致。因此，作为对照，本文训练了一个简单的四层卷积神经网络，其参数量与大型学习核模型几乎相同。结果发现，即使在参数量相当的情况下，深度神经网络在低数据量情况下也难以有效学习，性能接近随机水平，而本文的方法在不同参数量下均能保持稳定的性能（见表4）。这一现象在 Jia-CNN 模型的不同参数规模上也显而易见，不过值得注意的是，Jia-CNN3 在低数据量下的表现优于 ResNet-16。

5.2.2 可解释性

为展示本文方法在分类任务中内置的可解释性，本文训练了一个大型学习核模型，用于在 Zheng 等人的素材集上区分一度房室传导阻滞 [1º Atrioventricular Block] 和窦性心律 [Sinus Rhythm]。随后，应用算法1为每个类别生成贡献图。研究发现，本文的重要性图谱能够可靠地将 PR 间期（决定性特征）识别为对一度房室传导阻滞分类贡献最大的因素，尽管模型从未被明确告知这一信号特征（见图5）。重要的是，这并非一种事后解释方法（如 SHAP 或 GradCAM），那些方法试图解释模型行为但无法保证忠实于模型内部决策过程。而本文的方法通过数值计算，精确地给出了信号每个部分对分类结果的具体贡献。

图5：精选的ECG解读案例。来自 Zheng 等人数据集的多个一度房室传导阻滞示例，以及通过算法1计算得到的相应贡献图。红色表示对一度房室传导阻滞分类的贡献更大，蓝色表示贡献较小。

6. Discussion

本文提出了一种面向医疗信号处理的轻量级架构，在保持与深度学习方法相当甚至更优性能的同时，兼具可解释性和高效性。通过PPG伪迹检测和单导联ECG房颤检测两个典型任务验证表明，该技巧在多个关键指标上展现出显著优势。

在PPG伪迹检测任务中，本办法在三个基准数据集上取得了接近最先进的性能，且参数数量比深度学习方式少数个数量级。特别值得注意的是，在最具挑战性的TROIKA资料集上，模型展现出优异的分布外泛化能力。SMoLK模型的结构简洁性和内在可解释性，使研究者能够直接探查每个卷积核对最终预测的贡献机制。该方法对计算和内存的极低需求，与基于深度学习的方法形成鲜明对比，为低功耗可穿戴设备实现高质量信号评估提供了可行性。

研究结果表明，SMoLK模型能有效捕捉识别优质和劣质PPG信号的关键特征，实现了可直接解释、轻量级且高性能的分类架构。对卷积核重要性的分析揭示，较大尺寸卷积核主要识别劣质信号特征，而较小尺寸卷积核负责捕捉正常PPG特征。在ECG分类任务中，模型展现出精准的特征识别能力，能够正确标识心律失常的界定特征。这些发现与现有研究共识一致，表明对于某些复杂任务，简单可解释模型同样能实现与深度神经网络相媲美的性能。

针对可穿戴设备的严格功耗限制，本文开发的参数削减技术有效优化了计算性能比。实验证明，在PPG分割任务中，即使移除大型模型超过22%的参数，仍能维持98%以上的原始性能（附录表6）。得益于模型的方便性和近乎线性特性，可直接对模型权重进行无损量化，这与深度神经网络复杂的量化流程形成鲜明对比。

经过优化后，本文最大模型在float16精度下内存占用低于100 KB，剪枝后可进一步降至75 KB以下；最小模型内存占用甚至低于3 KB。在计算效率方面，最大模型处理每秒信号仅需约1000万次浮点运算。这种内存高效且计算高效的特性，使得在微控制器等资源受限设备上达成最先进的PPG信号质量评估成为可能。特定值得一提的是，对于分割任务，SMoLK的输出仅依赖于输入信号的局部信息，无需等待大段信号采集即可建立实时计算。

，本研究采用的评估数据集存在一定局限性。在性能表现最差的测试样本中，观察到就是需要指出的标签质量问题可能限制了性能上限。此外，尽管在PPG任务中运用了多个留出集验证途径通用性，但受试者数量较少限制了统计效力，需要在更广泛人群中进行验证。虽然通过TROIKA等材料集评估了模型对运动伪迹的鲁棒性，但全面评估所有可能噪声源的鲁棒性仍是不现实的。本文方法乃至整个领域的发展，都将受益于在更大规模、更多样化的数据集上进行验证。

综上所述，本文方法为医疗信号处理提供了一条鲁棒、可解释且高效的科技路径，在保持与深度学习方法竞争性能的同时，特殊适合部署在低功耗设备上。未来研究可探索将该方式扩展至其他生理信号处理任务，并将其集成到消费级脉搏血氧仪、智能戒指、智能手表等低功耗设备中，为完成生物标志物的连续实时监测提供关键技术支撑。

7 Data Availability

The data has been made publicly available at https://doi.org/10.5281/zenodo.13117608 [64]. We refer to the original works [46-51] for the unprocessed data, as well as maintain a copy of the pre-processed data in our GitHub repository [64] (https://github.com/SullyChen/SMoLK. The Computing in Cardiology dataset and Zheng et al. dataset are available on PhysioNet.org (https://physionet.org/content/challenge-2017/1.0.0/ and https://doi.org/10.13026/wgex-er52, respsectively).

8 Code Availability

The code has been made publicly available at https://doi.org/10.5281/zenodo.13117608, our GitHub repository [64]: https://github.com/SullyChen/SMoLK.

[46] Attila Reiss, Ina Indlekofer, Philip Schmidt, and Kristof Van Laerhoven. Deep ppg: Largescale heart rate estimation with convolutional neural networks. Sensors, 19(14), 2019.
[47] Philip Schmidt, Attila Reiss, Robert Duerichen, Claus Marberger, and Kristof Van Laerhoven. Introducing wesad, a multimodal dataset for wearable stress and affect detection. In Proceedings of the 20th ACM International Conference on Multimodal Interaction, ICMI ’18, page 400–408, New York, NY, USA, 2018. Association for Computing Machinery.
[48] Zhilin Zhang, Zhouyue Pi, and Benyuan Liu. Troika: A general framework for heart rate monitoring using wrist-type photoplethysmographic signals during intensive physical exercise. IEEE Transactions on Biomedical Engineering, 62(2):522–531, 2015.
[49] Gari D. Clifford, Chengyu Liu, Benjamin Moody, Li wei H. Lehman, Ikaro Silva, Qiao Li, A. E. Johnson, and Roger G. Mark. Af classification from a short single lead ecg recording: The physionet/computing in cardiology challenge 2017. In Computing in Cardiology (CinC), pages 1–4. IEEE, 2017.
[50] Jianwei Zheng, Huimin Chu, Daniele Struppa, Jianming Zhang, Sir Magdi Yacoub, Hesham El-Askary, Anthony Chang, Louis Ehwerhemuepha, Islam Abudayyeh, Alexander Barrett, Guohua Fu, Hai Yao, Dongbo Li, Hangyuan Guo, and Cyril Rakovski. Optimal multi-stage arrhythmia classification approach. Scientific Reports, 10(1):2898, 2020.
[51] Jianwei Zheng, Hangyuan Guo, and Huimin Chu. A large scale 12-lead electrocardiogram database for arrhythmia study (version 1.0.0). PhysioNet, 2022.