【数据结构】哈希表的理论与实现 - 教程

哈希表的理论

哈希表是一种基于哈希函数实现高效查找的数据结构，其核心思想是通过哈希函数将关键字映射到存储位置。

哈希表示例分析

12 18 21 24 33 45 67 72

21	45		24	18	12	33

哈希函数：除数留余法

数值	哈希计算 (mod 7)	结果位置	冲突情况
12	12 % 7	5	与33冲突
33	33 % 7	5	与12冲突
18	18 % 7	4	-
45	45 % 7	3	与24冲突
21	21 % 7	0	-
24	24 % 7	3	与45冲突

哈希冲突/哈希碰撞了。
解决办法：1、线性探测法 2、链地址法

哈希表的搜索操作： O(1)

18 % 7 = 4 arr[4] 18

45 % 7 = 3 arr[3]

45 % 7 = 3 arr[3] ≠ 45 产生哈希冲突了，线性探测法继续找 O(1) → O(n)

哈希冲突是不可避免的，怎么减少哈希冲突？(下面讲的是线性探测法)

1、哈希函数。 如，除留余数法 让哈希表（桶）的长度：素数

2、哈希表的装载因子。 loadfactor = 已占用的桶的个数/桶的总个数 > 阈值（0.75）——→ 哈希表就需要扩容了。相当于数组的扩容（对于线性探测哈希表来说），原来哈希表中的元素，需要在新的哈希表中重新哈希。—— O(n)

均摊时间复杂度 O(1)

线性探测哈希表

增加元素：

通过哈希函数计算数据存放的位置

该位置空闲，直接存储元素，完成

该位置被占用，从当前位置向后找空闲的位置，存放该元素

查询元素：

通过哈希函数计算数据存放的位置，从该位置取值（判断状态 STATE_USEING）

该值==要查询的元素值，找到了！

该值 ≠ 要查询的元素值（之前往这个位置放元素时，发生哈希冲突了），继续遍历往后找该元素

【补充】往后遍历到什么时候结束呢？

位置是空的有两种情况：1、这个位置是空的，没放过元素 （不需要继续往后搜索） 2、这个位置是空的，以前放过元素，后来被删除了（需要继续往后搜索）

会发现桶里面只放元素是不行的，还要放桶的状态

struct Node{

int val;

State state; //当前位置的状态

}

enumState{

STATE_USEING, //正在使用

STATE_UNUSE, //从来没用过

STATE_DEL //当前位置的元素被删除

}

删除元素：

通过哈希函数计算数据存放的位置，从该位置取值，判断状态STATE_USING

该值==要删除的值，直接修改当前位置的状态就可以 STATE_DEL

该值 ≠ 要删除的值，继续往后遍历，找到该元素，修改状态，如果遇到 STATE_UNUSE，结束

实现：

#include <iostream>
  using namespace std;
  enum State{
  STATE_UNUSE,    //从未使用过的桶
  STATE_USING,    //正在使用的桶
  STATE_DEL,      //元素被删除了的桶
  };
  //桶的类型
  struct Bucket{
  Bucket(int key = 0, State state = STATE_UNUSE)
  : key_(key)
  , state_(state)
  {}
  int key_;     //存储的数据
  State state_;     //桶的当前状态
  };
  //线性探测哈希表类型
  class HashTable{
  public:
  HashTable(int size = primes_[0], double loadFactor = 0.75)
  : useBucketNum_(0)
  , loadFactor_(loadFactor)
  , primeIdex_(0)
  {
  //把用户传入的size调整到最近的比较大的素数上
  if(size != primes_[0]){
  for(; primeIdex_ < PRIME_SIZE; primeIdex_++){
  if(primes_[primeIdex_] > size)
  break;
  }
  //用户传入的size过大，已经超过最后一个素数，调整到最会一个素数
  if(primeIdex_ == PRIME_SIZE){
  primeIdex_--;
  }
  }
  tableSize_ = primes_[primeIdex_];
  table_ = new Bucket[tableSize_];
  }
  ~HashTable(){
  delete[]table_;
  table_ = nullptr;
  }
  public:
  //插入元素
  bool insert(int key){
  //考虑扩容
  double factor = useBucketNum_*1.0 / tableSize_;
  cout << "factor:" << factor << endl;
  if(factor > loadFactor_){
  //哈希表开始扩容
  expand();
  }
  int idx = key % tableSize_;
  int i = idx;
  do{
  if(table_[i].state_ != STATE_USING){
  table_[i].state_ = STATE_USING;
  table_[i].key_ = key;
  useBucketNum_++;
  return true;
  }
  i = (i+1)%tableSize_;
  }while(i != idx);
  return false;
  }
  //删除元素
  bool erase(int key){
  int idx = key % tableSize_;
  int i = idx;
  do{
  if(table_[i].state_ == STATE_USING && table_[i].key_ == key){
  table_[i].state_ = STATE_DEL;
  useBucketNum_--;
  }
  i = (i+1) % tableSize_;
  }while(table_[i].state_ != STATE_UNUSE && i != idx);
  return true;
  }
  //查询
  bool find(int key){
  int idx = key % tableSize_;
  int i = idx;
  do{
  if(table_[i].state_ == STATE_USING && table_[i].key_ == key){
  return true;
  }
  i = (i+1) % tableSize_;
  }while(table_[i].state_ != STATE_UNUSE && i != idx);
  return false;
  }
  private:
  void expand(){
  ++primeIdex_;
  if(primeIdex_ ==  PRIME_SIZE){
  throw "HashTable is too large! can not expand anymore!";
  }
  Bucket* newTable = new Bucket[primes_[primeIdex_]];
  for(int i = 0; i < tableSize_; i++){
  if(table_[i].state_ == STATE_USING){   //旧表有效数据放到新表
  int idx = table_[i].key_ % primes_[primeIdex_];
  int k = idx;
  do{
  if(newTable[k].state_ != STATE_USING){
  newTable[k].state_ = STATE_USING;
  newTable[k].key_ = table_[i].key_;
  break;
  }
  k = (k+1) % primes_[primeIdex_];
  }while(k != idx);
  }
  }
  delete[]table_;
  table_ = newTable;
  tableSize_ = primes_[primeIdex_];
  }
  private:
  Bucket* table_;      //指向动态开辟的哈希表
  int tableSize_;      //哈希表当前的长度
  int useBucketNum_;   //已经使用的桶的个数
  double loadFactor_;  //哈希表的装载因子
  static const int PRIME_SIZE = 10;   //素数表的大小
  static int primes_[PRIME_SIZE];    //素数表
  int primeIdex_;                   //当前使用的素数下标
  };
  int HashTable::primes_[PRIME_SIZE] = {3, 7, 23, 47, 97, 251, 443, 911, 1471, 42773};
  int main(){
  HashTable htable;
  htable.insert(21);
  htable.insert(32);
  htable.insert(14);
  htable.insert(15);
  htable.insert(22);
  cout << htable.find(14) << endl;
  htable.erase(14);
  cout << htable.find(14) << endl;
  return 0;
  }

链式哈希表

线性探测哈希表的缺陷：

1、发生哈希冲突时，靠近O(n)的时间复杂度，存储变慢

2、多线程环境中，线性探测所用到的基于数组实现的哈希表，只能给全局的表用互斥锁来保证哈希表的原子操作，保证线程安全！

链式哈希表可以用：分段的锁！既保证了线程安全，又有一定的并发量，提高了效率！

例如：12 18 21 24 33 45 67 72 哈希函数采用除留余数法，哈希表长度7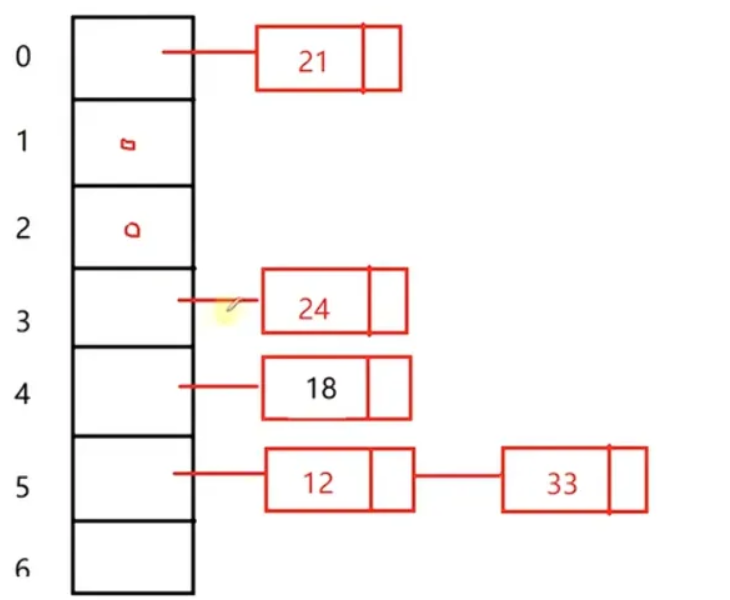

哈希表O(1) 无线趋近于O(1)—→哈希冲突的存在

每个桶的链表比较长，链表搜索花费的时间就大

优化一：当链表长度大于某个阈值时，把桶里面的这个链表转化成红黑树（搜索时间复杂度O(logn)）

优化二：链式哈希表每个桶都可以创建自己的互斥锁，不同桶中的链表操作，可以互斥起来

实现：

#include <iostream>
  #include <vector>
    #include <list>
      #include <algorithm>
        using namespace std;
        //链式哈希表
        class HashTable{
        public:
        HashTable(int size = primes_[0], double loadFactor = 0.75)
        : useBucketNum_(0)
        , loadFactor_(loadFactor)
        , primeIdex_(0)
        {
        if(size != primes_[0]){
        for(; primeIdex_ < PRIME_SIZE; primeIdex_++){
        if(primes_[primeIdex_] >= size){
        break;
        }
        }
        if(primeIdex_ == PRIME_SIZE)
        primeIdex_--;
        }
        table_.resize(primes_[primeIdex_]);
        }
        public:
        //增加元素  不能重复插入key
        void insert(int key){
        //判断扩容
        double factor = useBucketNum_*1.0/table_.size();
        cout << "factor:" << factor << endl;
        if(factor > loadFactor_){
        expand();
        }
        int idx = key % table_.size();
        if(table_[idx].empty()){
        useBucketNum_++;
        table_[idx].emplace_front(key);
        }
        else{
        //使用全局的::find泛型算法，而不是调用自己的成员方法
        auto it = ::find(table_[idx].begin(), table_[idx].end(), key);
        if(it == table_[idx].end()){
        //key不存在
        table_[idx].emplace_front(key);
        }
        }
        }
        //删除元素
        void erase(int key){
        int idx = key % table_.size();
        auto it = ::find(table_[idx].begin(), table_[idx].end(), key);
        if(it != table_[idx].end()){
        table_[idx].erase(it);
        if(table_[idx].empty()){
        useBucketNum_--;
        }
        }
        }
        //搜索元素
        bool find(int key){
        int idx = key % table_.size();
        auto it = ::find(table_[idx].begin(), table_[idx].end(), key);
        return it != table_[idx].end();
        }
        private:
        //扩容函数
        void expand(){
        if(primeIdex_ + 1 ==  PRIME_SIZE){
        throw "HashTable is too large! can not expand anymore!";
        }
        primeIdex_++;
        useBucketNum_ = 0;
        vector<list<int>> oldTable;
          //swap交换两个容器的成员变量（两个容器Allocator一样时），不涉及数据拷贝，效率很高 
          table_.swap(oldTable);   //table_ 与 oldTable交换后，table_变为空
          table_.resize(primes_[primeIdex_]);
          for(auto list : oldTable){
          for(auto key : list){
          int idx = key % table_.size();
          if(table_[idx].empty()){
          useBucketNum_++;
          }
          table_[idx].emplace_front(key);
          }
          }
          }
          private:
          vector<list<int>> table_;
            int useBucketNum_;      //记录使用的桶的个数
            double loadFactor_;     //记录哈希表的装载因子
            static const int PRIME_SIZE = 10;   //素数表的大小
            static int primes_[PRIME_SIZE];    //素数表
            int primeIdex_;                 //当前使用的素数下标
            };
            int HashTable::primes_[PRIME_SIZE] = {3, 7, 23, 47, 97, 251, 443, 911, 1471, 42773};
            int main(){
            HashTable htable;
            htable.insert(21);
            htable.insert(32);
            htable.insert(14);
            htable.insert(15);
            htable.insert(22);
            htable.insert(23);
            cout << htable.find(15) << endl;
            htable.erase(15);
            cout << htable.find(15) << endl;
            return 0;
            }

哈希表总结

哈希表的核心定义：存储位置=f(关键字) 一个关键字通过散列函数进行映射，得到其存储位置。这种技术称为散列技术。f称为哈希函数或者散列函数。采用散列技术将记录存储在一块连续的存储空间中，这块连续的存储空间称为哈希表。

优势：快速查找，时间复杂度O(1)

缺点：链式哈希表每一个节点既要存数据，又要存地址，内存空间占用了比较大。空间换时间。

散列函数：

设计特点： 计算简单（复杂度会降低查找的时间）、散列地址分布均匀（减少哈希冲突）