实用指南：[数据结构] 队列实战！火车车厢重排从 0 到 1：缓冲轨巧用 + 可运行代码

队列实战！火车车厢重排从0到1：缓冲轨巧用+可运行代码（附测试验证）

刚做队列应用实验时，我对着火车车厢重排的示意图卡了好久：入轨、缓冲轨、出轨三个队列到底怎么配合？明明车厢编号是1~9的连续数，却不知道什么时候该把车厢暂存到缓冲轨，什么时候该输出到出轨，连“3692471850”这个测试用例都跑不出123456789的结果。后来才发现，核心就是利用队列“先进先出”的特性，让缓冲轨当“临时仓库”，每一步都盯着“下一个要出的编号”（nowOut）来运行。

今天就把这份《算法与数据结构》的解题思路拆成“新手友好版”，从转轨站结构讲到代码落地，再到实测验证，全程大白话+可复制代码，确保你跟着做就能跑通车厢重排。

一、实验核心：要解除啥问题？转轨站咋工作？

实验题目：火车车厢重排。实验说明：转轨站示意图如下：

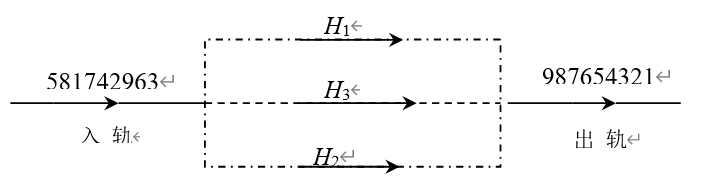火车车厢重排过程如下：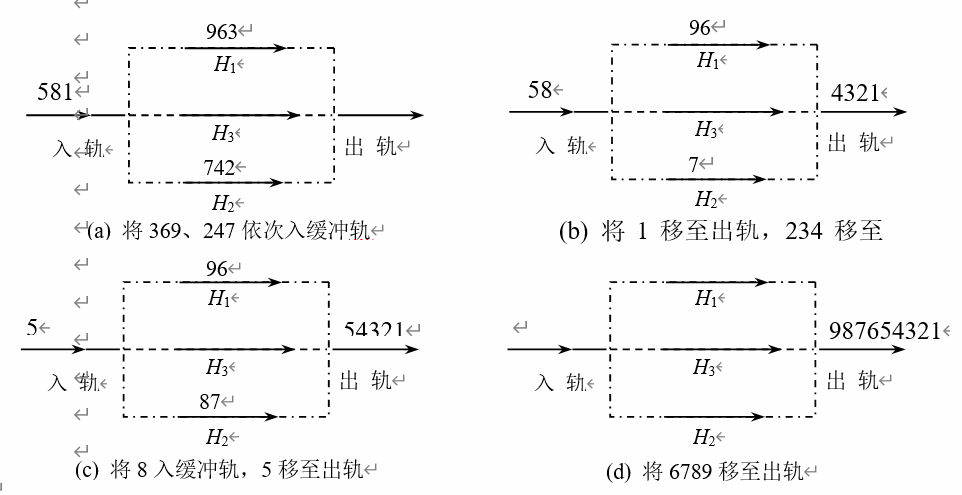

火车车厢重排算法伪代码如下：

1. 实验目标

给定一组连续编号（1~n）但顺序打乱的火车车厢（比如3、6、9、2、4、7、1、8、5），用队列模拟“转轨站”，把车厢重排成1、2、3…n的顺序，最终从“出轨”输出。

2. 转轨站结构（关键！先看懂再写代码）

实验里的转轨站有3类队列，作用各不相同，对应代码里的H1、H2、H3：

队列类型	代码中的队列	作用
入轨	H3	存放刚开始打乱的车厢序列（比如输入的369247185）
缓冲轨	H1、H2	暂存暂时不能输出到出轨的车厢，必须保证车厢编号大于队尾（比如H1队尾是2，只能放3、4…，后续才能有序出队）
出轨	无单独队列	最终输出有序车厢的“通道”，输出一个，下一个要输出的编号（nowOut）就+1

二、核心解题思路（3步走，大白话版）

整个重排逻辑围绕“下一个要输出的编号（nowOut）”展开，nowOut初始为1（第一个要输出的是1），然后循环处理直到所有队列都空：

步骤1：初始化准备

• 初始化3个队列：H1（缓冲轨1）、H2（缓冲轨2）、H3（入轨）；
• 把用户输入的打乱车厢（以0结束）依次放入H3；
• 定义nowOut = 1，记录下一个要输出到出轨的车厢编号。

步骤2：循环处理车厢（核心逻辑）

遍历H3（入轨），每一步做3件事：

1. 判断入轨队头能不能直接出：如果H3的队头编号 == nowOut，直接输出到出轨，nowOut+1（比如nowOut=1时，H3队头是1就输出，nowOut变2）；
2. 判断缓冲轨队头能不能出：若是H1或H2的队头 == nowOut，输出该车厢，nowOut+1（比如nowOut=2时，H2队头是2就输出）；
3. 入轨车厢放进缓冲轨：假设前两步都不能出，就把H3的队头放进H1或H2——要求是“车厢编号 > 缓冲轨队尾”（空缓冲轨可以直接放），保证后续能有序出队（比如H1队尾是3，只能放4、5…）。

步骤3：直到所有队列空

重复步骤2，直到H3（入轨）、H1（缓冲轨1）、H2（缓冲轨2）都为空，此时出轨已经输出1、2、3…n的有序序列。

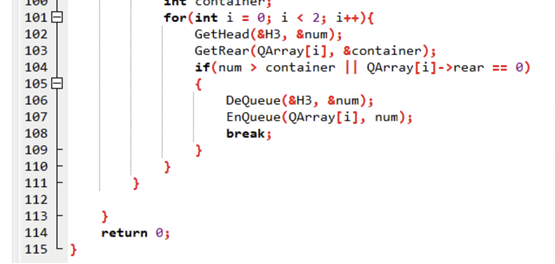
三、完整代码实现（补全原文错误，附详细注释）

原文代码有小问题（比如队列初始化没设front、return θ笔误），这里已修正，新手可直接复制运行：

#include <stdio.h>
  #define MAXSIZE 100  // 队列最大容量，足够应对实验需求
  typedef int SElemType;  // 车厢编号类型（整数）
  typedef int Status;     // 函数返回状态（0=失败，1=成功）
  // 队列结构体（顺序队列）
  typedef struct Queue {
  SElemType data[MAXSIZE];  // 存车厢编号
  int front;               // 队头指针（出队从front）
  int rear;                // 队尾指针（入队从rear）
  } Queue;
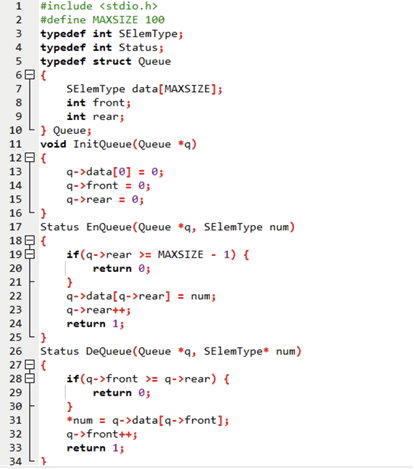
  // 1. 初始化队列（front和rear都设0，代表空队列）
  void InitQueue(Queue *q) {
  q->front = 0;    // 原文漏了front初始化，必须加上！
  q->rear = 0;
  // data[0]初始化没必要，队列用front和rear控制，不是靠data[0]
  }
  // 2. 入队（把编号num放进队列q）
  Status EnQueue(Queue *q, SElemType num) {
  // 队列满的判断：rear到最大容量-1（留一个位置防溢出，也可设为rear >= MAXSIZE）
  if (q->rear >= MAXSIZE - 1) {
  printf("队列满了，无法入队！\n");
  return 0;  // 原文是θ，修正为0
  }
  q->data[q->rear] = num;  // 队尾放元素
  q->rear++;               // 队尾后移
  return 1;
  }
  // 3. 出队（把队列q的队头元素存到num，成功返回1）
  Status DeQueue(Queue *q, SElemType* num) {
  // 队列空的判断：front == rear
  if (q->front >= q->rear) {
  // printf("队列空了，无法出队！\n");
  return 0;
  }
  *num = q->data[q->front];  // 取队头元素
  q->front++;                // 队头后移
  return 1;
  }
  // 4. 取队头元素（只看，不出队，存到num）
  Status GetHead(Queue *q, SElemType* num) {
  if (q->front >= q->rear) {
  return 0;
  }
  *num = q->data[q->front];
  return 1;
  }
  // 5. 取队尾元素（只看，不出队，存到num）
  Status GetRear(Queue *q, SElemType* num) {
  if (q->front >= q->rear) {
  return 0;
  }
  *num = q->data[q->rear - 1];  // 队尾是rear-1（因为rear指向空位置）
  return 1;
  }
  // 主函数：火车车厢重排逻辑
  int main() {
  Queue H1, H2, H3;  // H1=缓冲轨1，H2=缓冲轨2，H3=入轨
  InitQueue(&H1);
  InitQueue(&H2);
  InitQueue(&H3);
  Queue* bufferQueues[] = {&H1, &H2};  // 缓冲轨数组，方便循环遍历
  // 1. 输入打乱的车厢编号（输入0停止）
  printf("请输入火车车厢编号（连续整数，输入0停止）：\n");
  SElemType inputNum;
  while (1) {
  scanf("%d", &inputNum);
  if (inputNum == 0) {
  break;  // 输入0结束
  }
  EnQueue(&H3, inputNum);  // 放入入轨H3
  }
  // 2. 初始化下一个要输出的车厢编号（从1开始）
  int nowOut = 1;
  printf("\n出轨输出序列：");
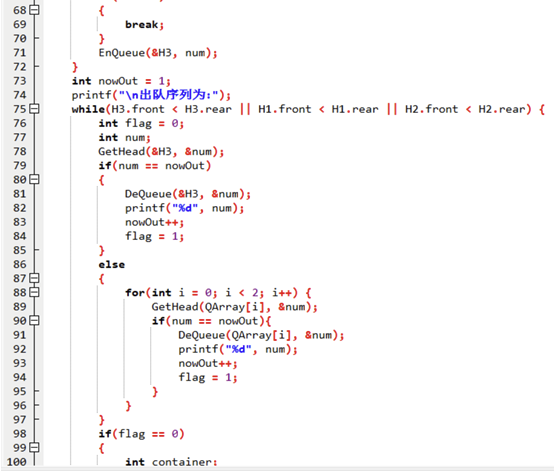
  // 循环处理：入轨、缓冲轨都为空才结束
  while (H3.front < H3.rear || H1.front < H1.rear || H2.front < H2.rear) {
  int isOutput = 0;  // 标记本次是否有车厢输出到出轨
  SElemType tempNum;  // 临时存车厢编号
  // 步骤1：判断入轨H3的队头能不能直接输出
  if (GetHead(&H3, &tempNum) && tempNum == nowOut) {
  DeQueue(&H3, &tempNum);  // 出队
  printf("%d ", tempNum);   // 输出到出轨
  nowOut++;                 // 下一个要输出的编号+1
  isOutput = 1;
  }
  // 步骤2：如果入轨不能出，看缓冲轨（H1、H2）的队头能不能出
  else {
  for (int i = 0; i < 2; i++) {  // 遍历两个缓冲轨
  if (GetHead(bufferQueues[i], &tempNum) && tempNum == nowOut) {
  DeQueue(bufferQueues[i], &tempNum);
  printf("%d ", tempNum);
  nowOut++;
  isOutput = 1;
  break;  // 输出一个即可，下一轮再判断其他
  }
  }
  }
  // 步骤3：如果都不能出，把入轨H3的队头放进合适的缓冲轨
  if (!isOutput) {
  GetHead(&H3, &tempNum);  // 取入轨当前要处理的车厢
  SElemType bufferRear;    // 缓冲轨的队尾编号
  // 遍历缓冲轨，找能放的（空缓冲轨 或 车厢编号>缓冲轨队尾）
  for (int i = 0; i < 2; i++) {
  if (bufferQueues[i]->front == bufferQueues[i]->rear) {  // 缓冲轨空
  DeQueue(&H3, &tempNum);
  EnQueue(bufferQueues[i], tempNum);
  break;
  } else {  // 缓冲轨非空，判断是否大于队尾
  GetRear(bufferQueues[i], &bufferRear);
  if (tempNum > bufferRear) {
  DeQueue(&H3, &tempNum);
  EnQueue(bufferQueues[i], tempNum);
  break;
  }
  }
  }
  }
  }
  printf("\n车厢重排完成！\n");
  return 0;
  }

四、运行测试：实测验证（和实验结果一致）

测试用例：输入3 6 9 2 4 7 1 8 5 0（输入0停止）

• 输入过程：运行程序后，依次输入3 6 9 2 4 7 1 8 5 0，按回车；

• 输出结果：出轨输出序列：1 2 3 4 5 6 7 8 9 车厢重排完成！；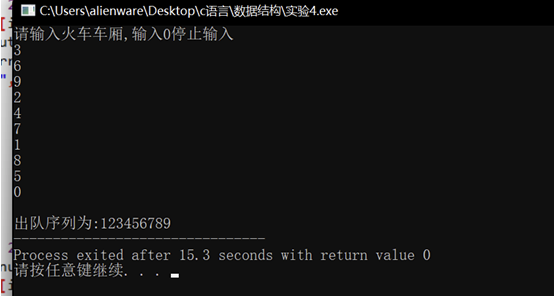
  

• 验证：完全符合“1~9有序”的要求，实验测试用例3692471850（即输入3 6 9 2 4 7 1 8 5 0）运行正确。

五、新手避坑指南（我踩过的坑，你别踩）

1. 缓冲轨放车厢必须“大于队尾”
   比如H1队尾是2，不能放1！否则1永远在2后面，当nowOut=1时，H1队头是2，1出不来，最后重排失败。这是实验的核心规则，必须遵守。

2. 队列初始化要设front=0
   原文代码的InitQueue只设了rear=0，漏了front=0，导致队列判断空/满出错，必须补上q->front=0。

3. nowOut要及时自增
   每次输出一个车厢后，一定要nowOut++，否则会一直重复输出同一个编号（比如一直找1，找到后不+1，下次还找1）。

4. 入轨遍历要“先判后出”
   处理入轨车厢时，先通过GetHead判断能不能出，再用DeQueue出队，不能直接DeQueue后再判断，否则会把不该出的车厢删掉。

六、总结：队列的核心价值&优化方向

1. 队列在实验中的作用

• 入轨（H3）：“先进先出”保证打乱的车厢按输入顺序处理；
• 缓冲轨（H1、H2）：“暂存+有序”，通过“车厢>队尾”的规则，确保后续能按1、2、3…的顺序出队；
• 出轨：“顺序输出”，最终得到有序序列。

2. 时间复杂度说明

原文提到“时间复杂度较高”，主要是因为每次处理都要遍历缓冲轨（H1、H2），最坏情况下时间复杂度是O(n*k)（n是车厢数，k是缓冲轨数）。优化方向可以是“记录缓冲轨队尾最大值”，不用每次遍历找合适的缓冲轨，减少循环次数。