机器学习模型中异常样本、特征的三种常见分类与鉴别方法 - 教程
2025-10-13 16:23 tlnshuju 阅读(35) 评论(0) 收藏 举报
0 笔记
总结文章Outliers, Leverage, Residuals, and Influential Observations
异常值可以有三种不同的表现方式:
- 异常特征:观察值的特征与其他值显著不同。
- 不符合模型:观察值与预测模型的拟合度较差。
- 影响模型:某些观察值对模型的影响较大
值得注意的是,异常值并不一定是坏事。它们可能包含更多信息,例如,具有不同特征的真实用户或罕见行为。
杠杆(Leverage)
杠杆是用来衡量某个观察值与其他观察值的差异程度。杠杆值越高,表示该观察值对模型的影响越大。可以用以下公式计算杠杆值:
h i i = X i ( X T X ) − 1 X i T n h_{ii} = \frac{X_i (X^TX)^{-1} X_i^T}{n} hii=nXi(XTX)−1XiT
其中 X X X 是设计矩阵, n n n 是样本数量。
残差(Residuals)
残差是指模型预测值与实际观察值之间的差异。残差越大,说明模型对该观察值的预测越不准确。残差可以表示为:
e i = y i − y ^ i e_i = y_i - \hat{y}_i ei=yi−y^i
影响观察(Influential Observations)
影响观察是指移除某个观察值后,模型估计的变化显著。影响观察的计算可以用以下公式表示:
D i = β ^ − β ^ − i 1 − h i i D_i = \frac{\hat{\beta} - \hat{\beta}_{-i}}{1 - h_{ii}} Di=1−hiiβ^−β^−i
这里, β ^ \hat{\beta} β^ 是包含所有观察值的模型参数, β ^ − i \hat{\beta}_{-i} β^−i 是移除观察值 i i i 后的模型参数。
可以使用 Mermaid 图示来展示异常值的检测过程:
1 引言
在数据科学中,一个常见的任务是异常检测,即理解一个观测值是否 “不寻常” 。首先,什么是不寻常?
在本文中,我们将探讨观测值可能不寻常的三种不同方式:它可能具有不寻常的特征,它可能与模型不符,或者它可能在模型训练中具有特别大的影响力。我们将看到,在线性回归中,后一个特征是前两个特征的副产品。
重要的是,不寻常不一定是坏事。与其他所有观测值具有不同特征的观测值通常携带更多信息。我们也期望有些观测值与模型不符,否则,模型可能存在偏差(我们正在过拟合)。
然而,“不寻常”的观测值也更有可能由不同的数据生成过程产生。极端情况包括测量误差或欺诈,但其他情况可能更微妙,例如具有罕见特征或行为的真实用户。领域知识始终为王,仅仅因为统计原因而删除观测值绝不明智。
话虽如此,让我们来看看观测值可能“不寻常”的一些不同方式。
2 简单示例
假设我们是一个点对点在线平台,我们有兴趣了解我们的业务是否存在任何可疑情况。我们有关于用户在平台上花费的时间以及他们交易总价值的信息。有些用户可疑吗?
首先,让我们看看数据。我从 src.dgp 导入数据生成过程 dgp_p2p(),并从 src.utils 导入一些绘图函数和库。
from src.utils import *
from src.dgp import dgp_p2p
df = dgp_p2p().generate_data()
df.head()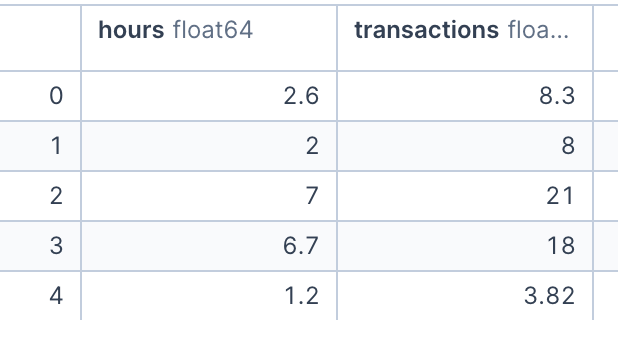
我们有 50 个用户的信息,我们观察到他们在平台上花费的 小时数 和总 交易额。由于我们只有两个变量,我们可以很容易地使用散点图来检查它们。
sns.scatterplot(data=df, x='hours', y='transactions').set(title='Data Scatterplot');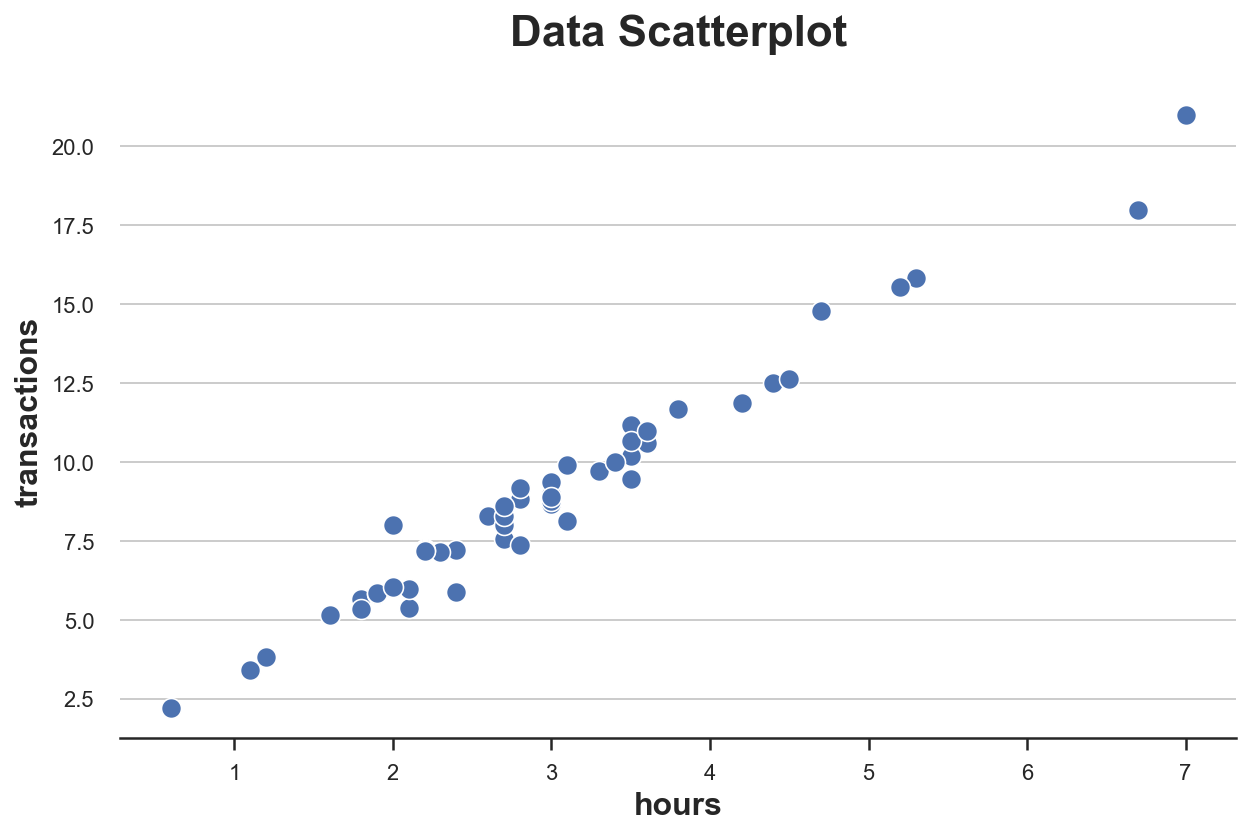
小时数 和 交易额 之间的关系似乎遵循清晰的线性关系。如果我们拟合一个线性模型,我们会观察到一个特别紧密的拟合。
smf.ols('hours ~ transactions', data=df).fit().summary().tables[1]
有没有哪个数据点看起来与其他点有可疑的差异?如何判断?
3 杠杆值
我们将用于评估“不寻常”观测值的第一个度量是杠杆值(leverage)。杠杆值的目的是捕捉单个点与其他数据点相比的差异程度。这些数据点通常被称为异常值(outliers),并且存在几乎无限量的算法和经验法则来标记它们。然而,其思想是相同的:标记在特征方面不寻常的观测值。
观测值 i i i 的杠杆值定义为
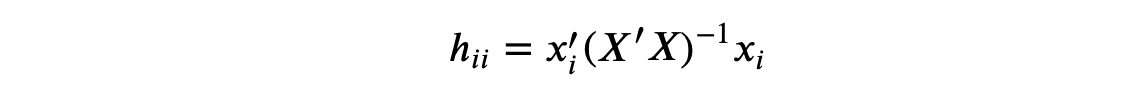
其中一个对杠杆值的解释是将其作为距离度量,其中单个观测值与所有观测值的平均值进行比较。
对杠杆值的另一个解释是观测值 i i i 的结果 y i y_i yi 对相应拟合值 y ^ i \hat{y}_i y^i 的影响。
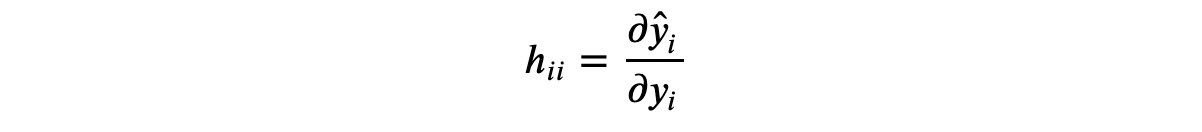
代数上,观测值 i i i 的杠杆值是设计矩阵 X ( X T X ) − 1 X T X(X^T X)^{-1} X^T X(XTX)−1XT 的第 i i i 个对角元素。在杠杆值的众多属性中,它们是非负的,并且它们的值之和等于 X X X 的维度(在我们的例子中为 1)。
让我们计算数据集中观测值的杠杆值。我们还标记了具有异常杠杆值的观测值(我们任意定义为偏离平均杠杆值两个标准差以上)。
X = np.reshape(df['hours'].values, (-1, 1))
Y = np.reshape(df['transactions'].values, (-1, 1))
df['leverage'] = np.diagonal(X @ np.linalg.inv(X.T @ X) @ X.T)
df['high_leverage'] = df['leverage'] > (np.mean(df['leverage']) + 2*np.std(df['leverage']))让我们绘制数据中杠杆值分布图。
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))
sns.histplot(data=df, x='leverage', hue='high_leverage', alpha=1, bins=30, ax=ax1).set(title='Distribution of Leverages');
sns.scatterplot(data=df, x='hours', y='transactions', hue='high_leverage', ax=ax2).set(title='Data Scatterplot');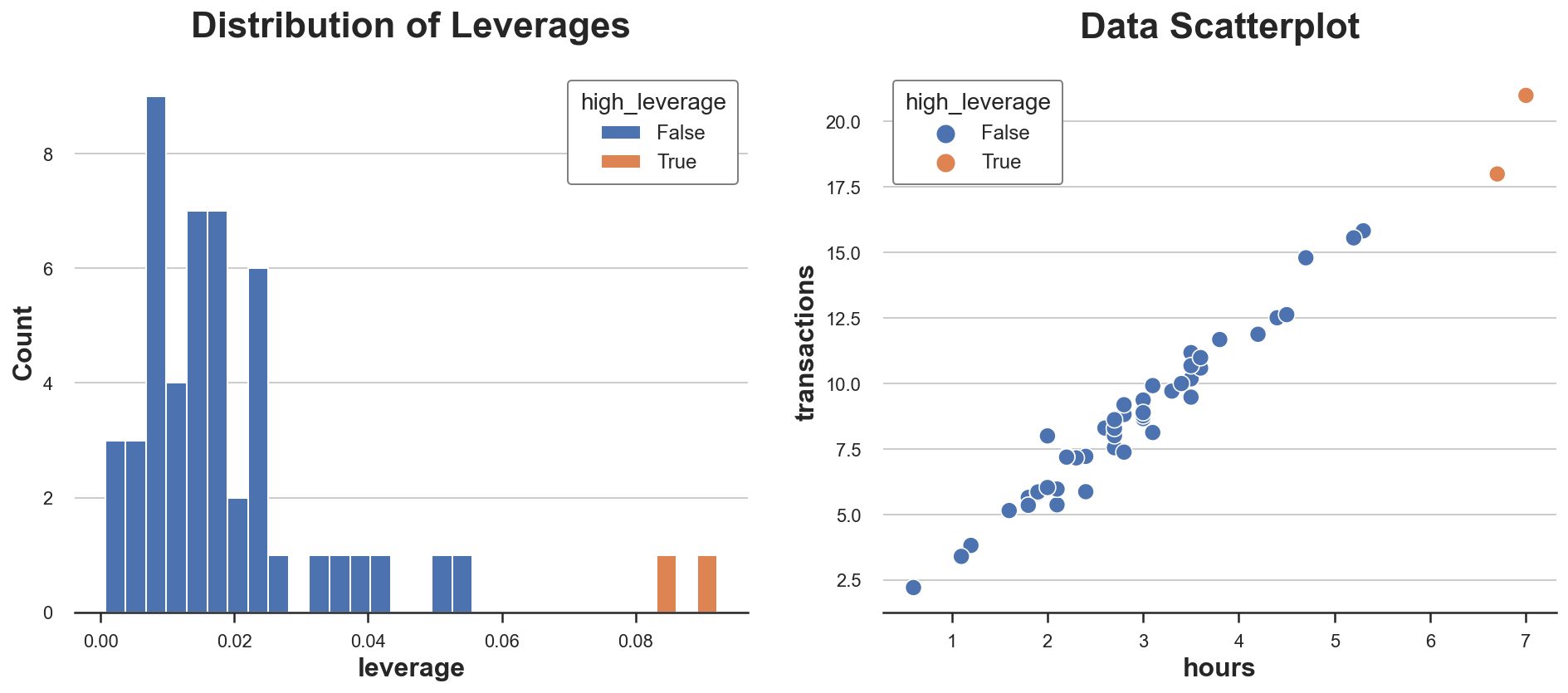
正如我们所看到的,分布是偏斜的,有两个观测值具有异常高的杠杆值。事实上,在散点图中,这两个观测值与其余分布略有分离。
这是坏消息吗?这取决于情况。异常值本身不是问题。实际上,如果它们是真实的观测值,它们可能比其他观测值携带更多的信息。另一方面,它们也更有可能不是真实的观测值(例如欺诈、测量误差等)或者与其他观测值本质上不同(例如专业用户与业余用户)。无论如何,我们可能需要进一步调查并尽可能多地利用特定情境的信息。
绝不应仅仅因为统计原因而删除观测值
重要的是,观测值具有高杠杆值的事实告诉我们关于模型特征的信息,但与模型本身无关。这些用户只是不同,还是他们的行为也不同?
4 残差
到目前为止,我们只谈论了不寻常的特征,但不寻常的行为呢?这就是回归残差所衡量的。
回归残差是预测结果值与观察结果值之间的差异。从某种意义上说,它们捕捉了模型无法解释的部分:一个观测值的残差越高,它在模型无法解释的意义上就越不寻常。
在线性回归中,残差可以写成
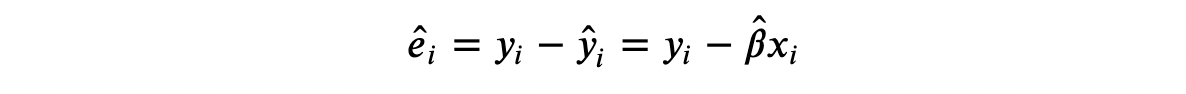
在我们的例子中,由于
X
X
X 是一维的(小时数),我们可以很容易地将它们可视化为观测值与预测线之间的距离。
Y_hat = X @ np.linalg.inv(X.T @ X) @ X.T @ Yplt.scatter(X, Y, s=50, label='data')
plt.plot(X, Y_hat, c='k', lw=2, label='prediction')
plt.vlines(X, np.minimum(Y, Y_hat), np.maximum(Y, Y_hat), color='r', lw=3, label="residuals");
plt.legend()
plt.title(f"Regression prediction and residuals");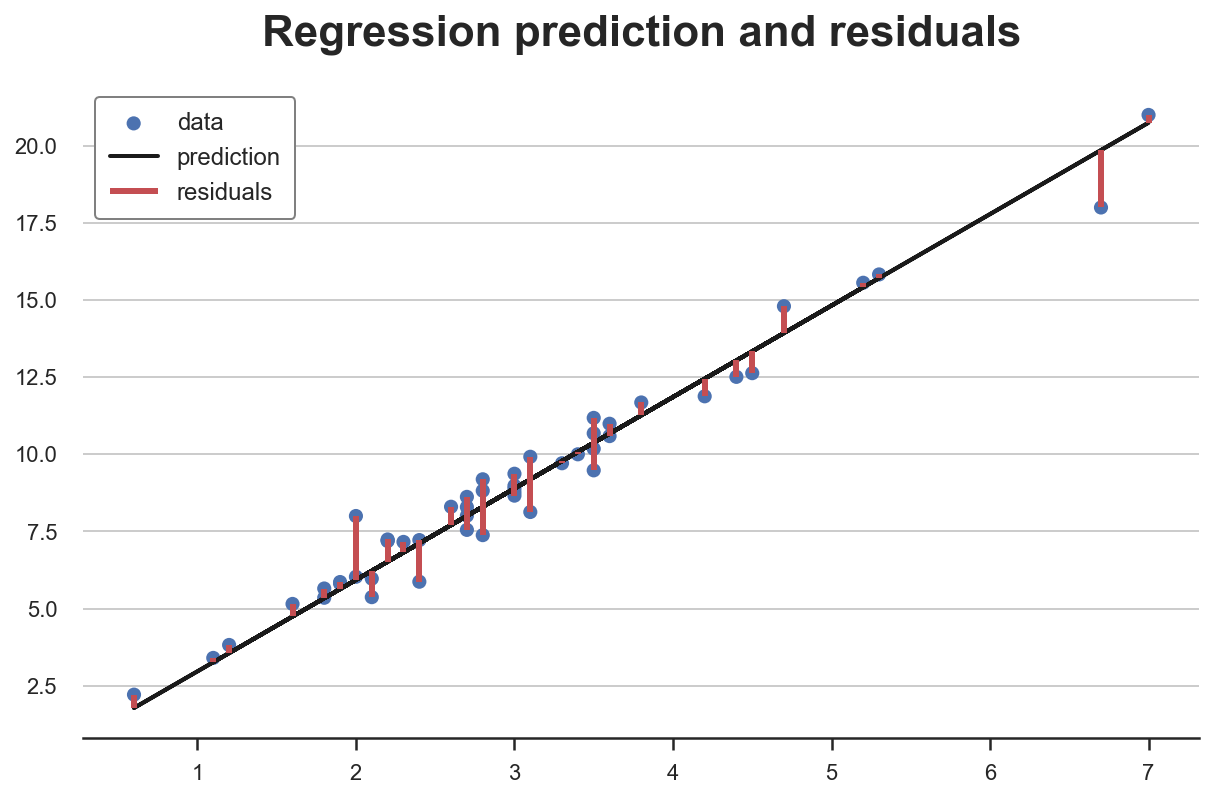
有些观测值有异常高的残差吗?让我们绘制它们的分布图。
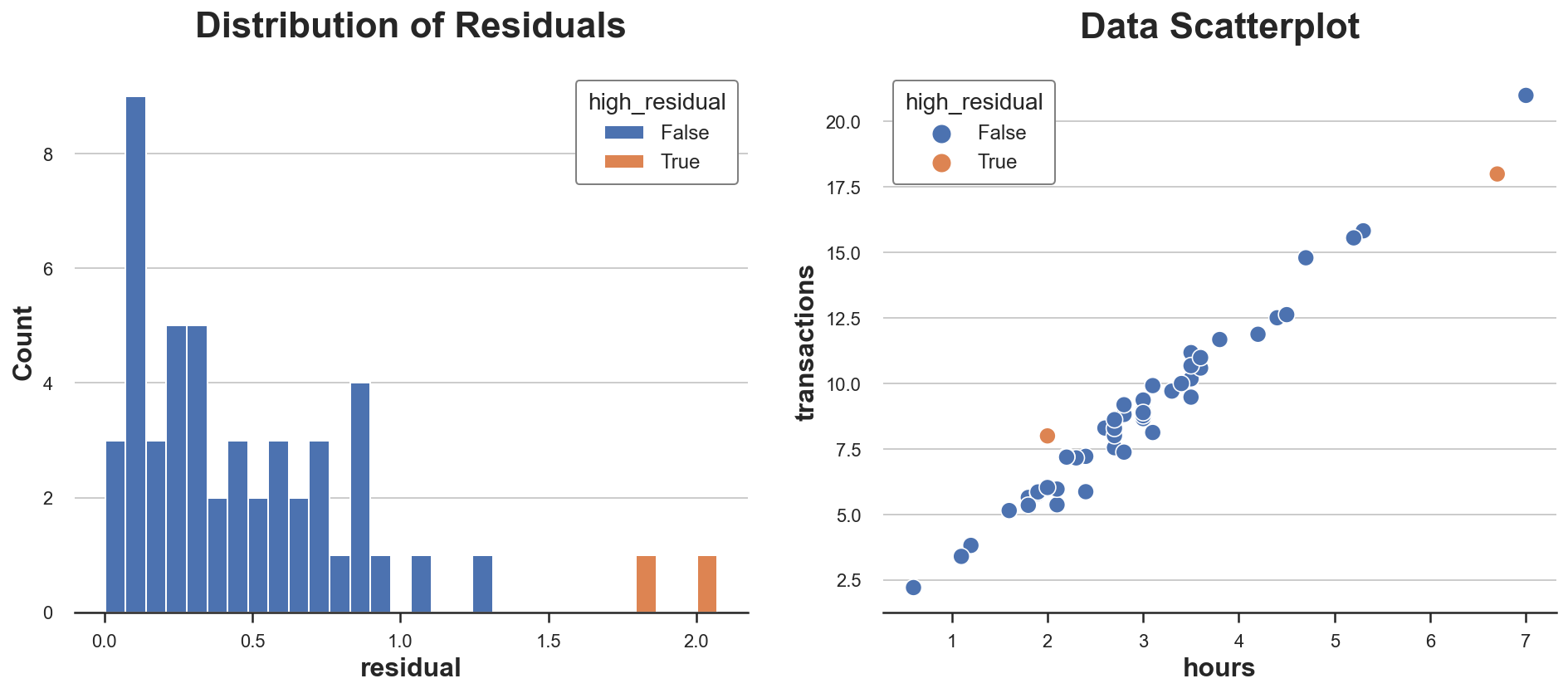
有两个观测值具有特别高的残差。这意味着对于这些观测值,模型在预测观察结果方面表现不佳。
这是坏消息吗?同样,不一定。一个过于完美地拟合观测值的模型很可能存在偏差。然而,理解为什么有些用户在花费时间和总交易额之间存在不同的关系仍然很重要。像往常一样,领域知识是关键。
到目前为止,我们已经研究了具有“不寻常”特征和“不寻常”行为的观测值,这些都是基于模型的。但是模型从何而来?我们的模型有多少是由少数观测值驱动的?是哪些观测值?
5 影响力
影响力(influence)和影响力函数(influence functions) 的概念正是为了回答这个问题而开发的:哪些是有影响力的观测值?这个问题在 80 年代非常流行,但后来长期失去吸引力,直到最近,由于解释复杂机器学习和人工智能模型的日益增长的需求,它又重新受到关注。
一般的想法是,如果删除一个观测值会显著改变估计模型,那么这个观测值就被定义为有影响力的。在线性回归中,我们将观测值 i i i 的影响力定义为:
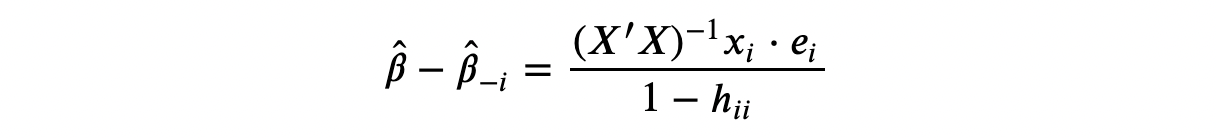
其中 β ^ − i \hat{\beta}_{-i} β^−i 是省略观测值 i i i 后估计的 OLS 系数。
正如你所看到的,它与杠杆值 h i i h_{ii} hii 和残差 e i e_i ei 都存在紧密的联系:影响力在这两者中都是递增的。事实上,在线性回归中,高杠杆值的观测值既是异常值,也具有高残差。这两个条件中的任何一个单独都不足以使一个观测值对模型产生影响力。
我们可以在数据中最好地看到这一点。
df['influence'] = (np.linalg.inv(X.T @ X) @ X.T).T * np.abs(Y - Y_hat)
df['high_influence'] = df['influence'] > (np.mean(df['influence']) + 2*np.std(df['influence']))
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))
sns.histplot(data=df, x='influence', hue='high_influence', alpha=1, bins=30, ax=ax1).set(title='Distribution of Influences');
sns.scatterplot(data=df, x='hours', y='transactions', hue='high_influence', ax=ax2).set(title='Data Scatterplot');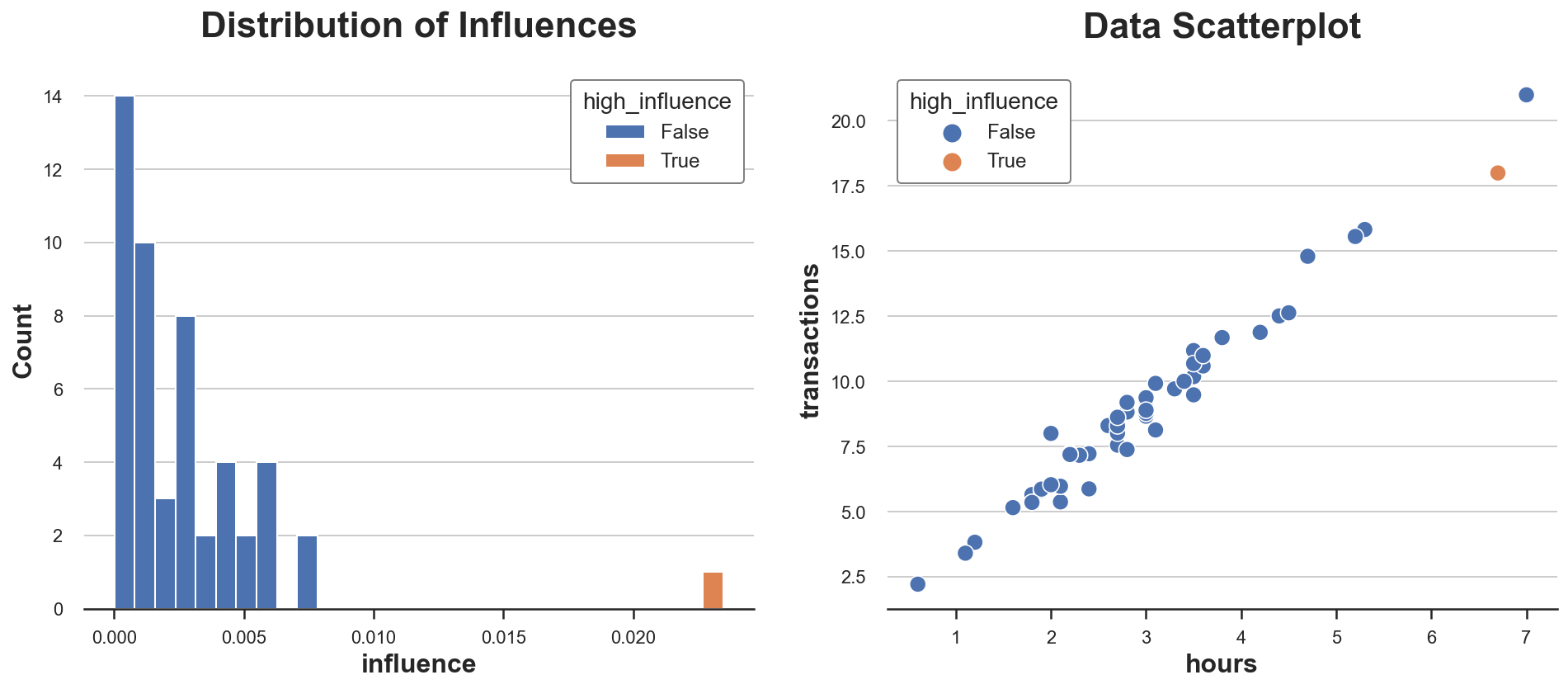
在我们的数据集中,只有一个观测值具有高影响力,其值比所有其他观测值的影响力不成比例地大。你仅凭散点图能猜到吗?
我们现在可以将所有“不寻常”的点绘制在同一张图上。我还将每个点的残差和杠杆值绘制在单独的图上。
def plot_leverage_residuals(df):
# Hue
df['type'] = 'Normal'
df.loc[df['high_residual'], 'type'] = 'High Residual'
df.loc[df['high_leverage'], 'type'] = 'High Leverage'
df.loc[df['high_influence'], 'type'] = 'High Influence'
# Init figure
fig, (ax1,ax2) = plt.subplots(1,2, figsize=(12,5))
ax1.plot(X, Y_hat, lw=1, c='grey', zorder=0.5)
sns.scatterplot(data=df, x='hours', y='transactions', ax=ax1, hue='type').set(title='Data')
sns.scatterplot(data=df, x='residual', y='leverage', hue='type', ax=ax2).set(title='Metrics')
ax1.get_legend().remove()
sns.move_legend(ax2, "upper left", bbox_to_anchor=(1.05, 0.8));
plot_leverage_residuals(df)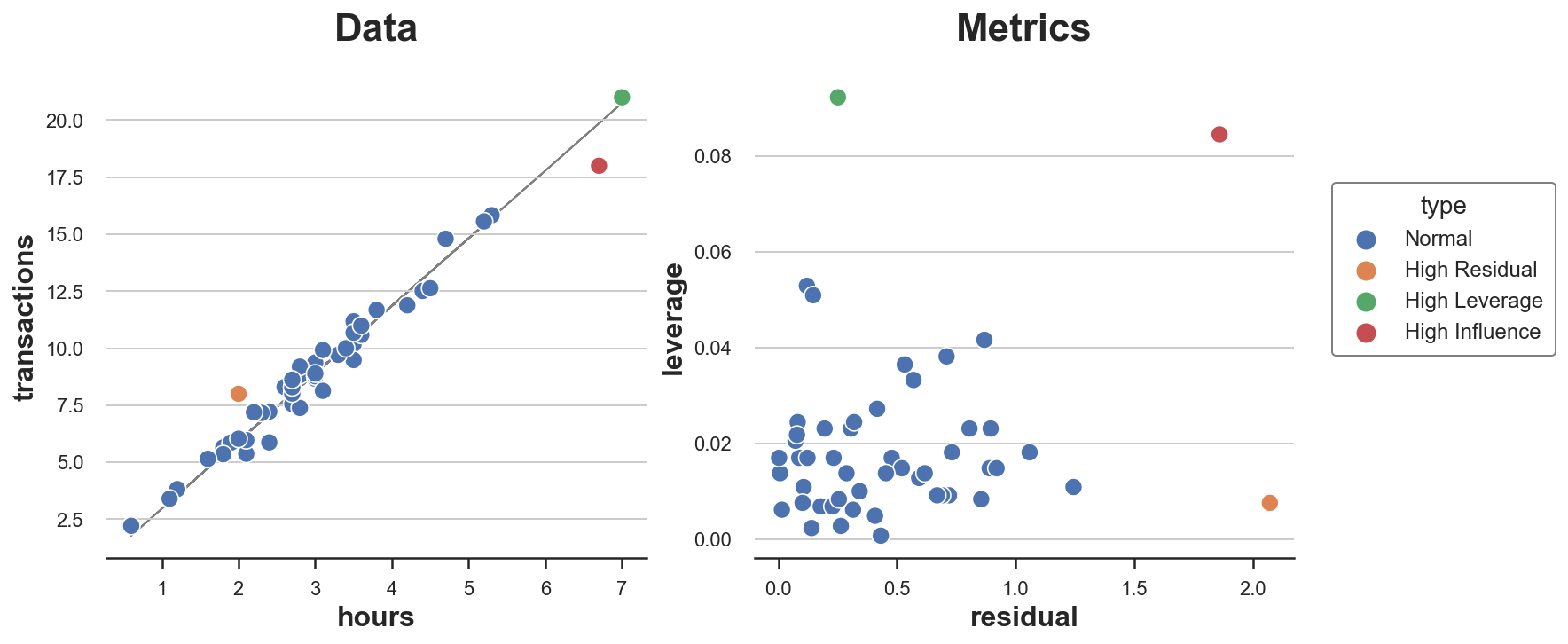
正如我们所看到的,我们有一个点具有高残差和低杠杆值,一个点具有高杠杆值和低残差,只有一个点同时具有高杠杆值和高残差:这是唯一有影响力的点。
从图中也可以清楚地看出,为什么这两个条件中的任何一个单独都不足以使一个观测值具有影响力并扭曲模型。橙色点具有高残差,但它位于分布的中间,因此不能倾斜最佳拟合线。绿色点则具有高杠杆值,并且远离分布中心,但它与拟合线完美对齐。删除它不会改变任何东西。而红色点在特征和行为上都与其他点不同,因此它将拟合线拉向自身。
6 结论
在这篇文章中,我们看到了观测值可能“不寻常”的几种不同方式:它们可能具有不寻常的特征或不寻常的行为。在线性回归中,当一个观测值同时具备这两种情况时,它也具有影响力:它会将模型拉向自身。
在本文的示例中,我们专注于单变量线性回归。然而,影响力函数的研究最近成为一个热门话题,因为需要使黑盒机器学习算法可理解。对于拥有数百万参数、数十亿观测值和剧烈非线性的模型,很难确定单个观测值是否具有影响力以及如何具有影响力。
7 参考文献
1 1 1 D. Cook, Detection of Influential Observation in Linear Regression (1980), Technometrics.
2 2 2 D. Cook, S. Weisberg, Characterizations of an Empirical Influence Function for Detecting Influential Cases in Regression (1980), Technometrics.
3 3 3 P. W. Koh, P. Liang, Understanding Black-box Predictions via Influence Functions (2017), ICML Proceedings.
8 代码
你可以在这里找到原始的 Jupyter Notebook:outliers.ipynb



 浙公网安备 33010602011771号
浙公网安备 33010602011771号