好的，我们来详细拆解图片中关于​​计算复杂度​​的分析。核心结论是：文中描述的线性Attention方案，其计算复杂度为 ​​O(nd²)​​。这意味着计算量随着序列长度n​​线性增长​​，而不是像标准Softmax Attention那样​​平方增长​​。关键在于 ​​d是固定的模型超参数（隐藏层维度）​​，而n是变化的序列长度。​​d是常数​​：在模型设计好后，隐藏层的维度d - 实践

文章阅读笔记：https://kexue.fm/archives/11033

一、为什么是线性注意力

好的，我们来详细拆解图片中关于​​计算复杂度​​的分析。

核心结论是：文中描述的线性Attention方案，其计算复杂度为 ​​O(nd²)​​。这意味着计算量随着序列长度 n ​​线性增长​​，而不是像标准Softmax Attention那样​​平方增长​​。

---

1. 复杂度分析（分步详解）

公式为 O = (QKᵀ)V，并通过结合律将其重写为 O = Q(KᵀV)。计算分两步进行：

第一步：计算 P = KᵀV

• ​​操作​​：矩阵 K 的转置（维度为 d×n）乘以矩阵 V（维度为 n×d）。
• ​​维度变化​​：(d×n) × (n×d) = d×d
• ​​计算量分析​​：
  • 结果矩阵 P 的每个元素都是 K 的一列（长度为 n）与 V 的一行（长度为 n）的内积。
  • 计算一个内积需要进行 n 次乘法和 n-1 次加法，近似为 O(n) 次操作。
  • 结果矩阵 P 有 d × d 个元素。
  • 因此，总计算量为：(d × d) × O(n) = O(n * d²)。

第二步：计算 O = QP

• ​​操作​​：矩阵 Q（维度为 n×d）乘以上一步的结果 P（维度为 d×d）。
• ​​维度变化​​：(n×d) × (d×d) = n×d
• ​​计算量分析​​：
  • 结果矩阵 O 的每个元素都是 Q 的一行（长度为 d）与 P 的一列（长度为 d）的内积。
  • 计算一个内积需要进行 d 次乘法和 d-1 次加法，近似为 O(d) 次操作。
  • 结果矩阵 O 有 n × d 个元素。
  • 因此，总计算量为：(n × d) × O(d) = O(n * d²)。

总复杂度

将两步的复杂度相加：O(nd²) + O(nd²) = O(nd²)。

---

“线性”复杂度？就是2. 为什么

关键在于 ​​d 是固定的模型超参数（隐藏层维度）​​，而 n 是变化的序列长度。

• ​​d 是常数​​：在模型设计好后，隐藏层的维度 d（例如512, 768, 1024等）就固定了。它不会随着输入序列的增长而变化。
• ​​n 是变量​​：输入序列的长度 n 可以变化，比如一个句子可以有10个词，也可以有1000个词。

因此，总复杂度 O(nd²) 可以看作是：
O(nd²) = d² * O(n)

由于 d² 是一个常数系数，所以整个计算量​​随着序列长度 n 线性增长​​，即 ​​O(n)​​。

---

3. 与标准Softmax Attention的对比

为了更好地理解为什么这种线性Attention更高效，我们对比一下标准Softmax Attention的计算步骤：

1. ​​计算注意力分数矩阵​​：A = QKᵀ
   • 维度：(n×d) × (d×n) = n×n
   • 计算量：O(n²d)
2. ​​应用Softmax和Mask（可选）​​：A' = softmax(A ⊙ M)
   • 对 n×n 矩阵的每一行进行Softmax，计算量：O(n²)
3. ​​加权求和​​：O = A'V
   • 维度：(n×n) × (n×d) = n×d
   • 计算量：O(n²d)

​​标准Attention的总复杂度为 O(n²d + n²d) = O(n²d)​​。

由于 d 是常数，复杂度主要取决于 n²。当序列长度 n 翻倍时，计算量会变为原来的​​4倍​​（平方增长）。而对于线性Attention，序列长度 n 翻倍，计算量仅变为原来的​​2倍​​（线性增长）。这在处理长序列（如长文档、高分辨率图像）时优势巨大。

总结

特性	标准Softmax Attention	文中线性Attention
​​核心运算​​	O = softmax(QKᵀ)V	O = (QKᵀ)V = Q(KᵀV)
​​复杂度​​	​​O(n²d)​​	​​O(nd²)​​
​​关于n的增长​​	​​平方增长 (O(n²))​​	​​线性增长 (O(n))​​
​​关键区别​​	必须计算并存储巨大的 n×n 注意力矩阵	通过结合律，避免了 n×n 矩阵，始终操作 d×d 或 n×d 矩阵

因此，文中的计算复杂度 O(nd²) 是通过​​矩阵乘法的结合律​​巧妙地避免计算庞大的 n×n 矩阵，将问题转化为两个复杂度仅为 O(nd²) 的矩阵乘法之和而得出的。

二、为什么相等

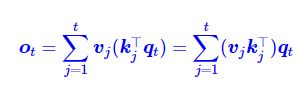
好的，我们来详细解释为什么图片中的这个等式成立。

ot​=∑j=1t​vj​(kj⊤​qt​)=∑j=1t​(vj​kj⊤​)qt​

这个等式成立的核心原因在于​​标量与矩阵相乘的结合律和分配律​​。我们可以从数学运算的优先级和维度分析两个角度来理解。

---

1. 从运算优先级和结合律角度理解

我们先来看等式中间的项：
v_j (k_jᵀ q_t)

• k_jᵀ 是一个 ​​行向量​​ (1×d 维)
• q_t 是一个 ​​列向量​​ (d×1 维)
• k_jᵀ q_t 的结果是这两个向量的​​内积（点积）​​。一个行向量乘以一个列向量，结果是一个​​标量​​（一个数字）。
• 因此，v_j (k_jᵀ q_t) 就是一个​​向量 v_j​​ 乘以一个​​标量​​。这在数学上是完全有效的，结果是将向量 v_j 的每个元素都放大这个标量倍。

现在再看等式最右边的项：
(v_j k_jᵀ) q_t

• v_j 是一个 ​​列向量​​ (d_v×1 维)
• k_jᵀ 是一个 ​​行向量​​ (1×d_k 维)
• v_j k_jᵀ 的结果是这两个向量的​​外积​​。一个列向量乘以一个行向量，结果是一个​​矩阵​​ (d_v×d_k 维)。
• 然后这个矩阵再乘以列向量 q_t (d_k×1 维)，结果得到一个​​列向量​​ (d_v×1 维)，这与等式左边的 o_t 维度一致。

​​为什么两者相等？​​
因为矩阵乘法满足结合律。我们可以把整个运算看作三个矩阵（向量）A = v_j, B = k_jᵀ, C = q_t 的连乘。结合律保证了：
(A * B) * C = A * (B * C)

• A * (B * C)： 先计算内积 (B * C)（得到一个标量），再让向量 A 乘以这个标量。
• (A * B) * C： 先计算外积 (A * B)（得到一个矩阵），再让这个矩阵乘以向量 C。

这两种计算路径的最终结果完全相同。

---

2. 依据一个简单的数值例子来验证

为了更直观地理解，我们假设向量都是二维的。

令：
v_j = [a, b]ᵀ (列向量)
k_j = [c, d]ᵀ -> 所以 k_jᵀ = [c, d] (行向量)
q_t = [e, f]ᵀ (列向量)

​​计算中间路径：v_j (k_jᵀ q_t)​​

1. 先计算内积：k_jᵀ q_t = [c, d] * [e, f]ᵀ = c*e + d*f (一个标量，记为 S)
2. 再计算：v_j * S = [a, b]ᵀ * S = [a*S, b*S]ᵀ = [a*(ce+df), b*(ce+df)]ᵀ

​​计算右边路径：(v_j k_jᵀ) q_t​​

1. 先计算外积：v_j k_jᵀ = [a, b]ᵀ * [c, d] = [[a*c, a*d], [b*c, b*d]] (一个2x2矩阵)
2. 再矩阵乘向量：[[a*c, a*d], [b*c, b*d]] * [e, f]ᵀ = [a*c*e + a*d*f, b*c*e + b*d*f]ᵀ = [a*(ce+df), b*(ce+df)]ᵀ

​​结论：​​ 两种计算方法得到了完全一样的结果 [a*(ce+df), b*(ce+df)]ᵀ。

---

3. 在注意力机制中的意义

这个等式在Transformer的线性注意力机制中至关重要，它实现了计算复杂度的“降维打击”。

• ​​原始方法（等式中间）​​：计算每个 j 时，都需要计算一个内积 (k_jᵀ q_t)（复杂度O(d)）然后乘以向量。对于从1到t的求和，总复杂度是 ​​O(t * d)​​。
• ​​创新方法（等式右边）​​：它揭示了一种全新的计算顺序。我们可以​​先​​将所有的 (v_j k_jᵀ) 加起来，​​再​​统一乘以 q_t。
  S_t = ∑(j=1 to t) (v_j k_jᵀ) （这是一个矩阵）
  o_t = S_t q_t （这是一个矩阵乘向量）

这种办法的巨大优势在于：

1. ​​状态复用​​：矩阵 S_t 可以通过递归公式 S_t = S_(t-1) + v_t k_tᵀ 来更新，而不需要存储所有的历史Key和Value。
2. ​​计算高效​​：计算输出 o_t 时，只需要做一次矩阵乘法 S_t q_t（复杂度O(d²)），而不再依赖于历史长度 t。这使得总复杂度从 ​​O(t * d)​​ 降为 ​​O(d²)​线性复杂度 ​就是​（对于每个时间步），对于整个序列就​O(n * d²)​​，远优于标准注意力的平方复杂度 ​​O(n² * d)​​。

总结

这个等式之所以成立，是​​基于矩阵乘法结合律这一基本数学原理​​。它绝不是一个近似或技巧，而是一个精确的、恒等的数学变换。

正是这个恒等式，为线性注意力模型供应了理论基础，使其能够将计算过程转化为一种类似RNN的递推形式，从而实现了计算效率的巨大提升，解决了传统Transformer模型在处理长序列时的核心瓶颈。

三、为什么相等

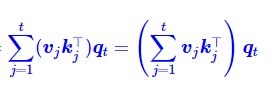
三、deltanet优化

好的，经过仔细分析苏剑林的这篇《线性注意力简史：从模仿、创新到反哺》，大家可以针对 ​​DeltaNet​​ 模型提出以下几个非常有潜力的改进方向。

DeltaNet的核心思想是使用​​Delta Rule​​（即在线学习中的最小均方算法）来更新状态矩阵 S_t，其公式为：
S_t = S_{t-1} + (v_t - S_{t-1} k_t) k_t^T

这是一个非常优雅的模型，但从文章的描述和其数学性质来看，仍有可以完善和探索的空间。

DeltaNet 的潜在改进方向

1. 引入数据依赖的遗忘门（Data-Dependent Gating）

• ​​当前局限​​：标准的DeltaNet没有显式的遗忘机制。它通过 (v_t - S_{t-1} k_t) 来“纠正”当前状态，这是一种隐式的、以误差驱动的更新。但对于序列建模，​​显式地、根据输入内容来决定遗忘多少旧信息​​往往更有效（如Mamba、GLA等模型所示）。
• ​​改进方案​​：借鉴 ​​Gated DeltaNet (GDN)​​ 和 ​​Mamba​​ 的思想，将更新规则中的学习率 η_t 或一个衰减因子 γ_t 变为由数据驱动的函数。
  • ​​公式改进​​：S_t = γ_t ⊙ S_{t-1} + η_t (v_t - S_{t-1} k_t) k_t^T
  • 其中，γ_t (遗忘门) 和 η_t (写入门) 可以是通过线性层或轻量级网络从当前输入 (k_t, v_t) 甚至当前状态 S_{t-1} 计算而来的向量或标量。这使模型能动态决定“记住多少”和“学习多少”。
• ​​挑战​​：保持模型的​​线性特性​​以利于高效并行训练。门控信号应仅依赖于当前输入，而不能引入对 S_{t-1} 的非线性依赖，否则会破坏其并行化能力。

2. 增强状态矩阵的表达能力

• ​​当前局限​​：DeltaNet的状态 S_t 是一个 d x d 的矩阵，它通过外积 v_t k_t^T 进行更新。这种方式的参数效率可能不是最高的，其表征能力可能存在上限。
• ​​改进方案​​：
  1. ​​多头DeltaNet（Multi-Scale DeltaNet）​​：将 k 和 v 的维度拆分到多个头（head）上，每个头独立运行DeltaNet规则。这相当于扩展了状态矩阵的“宽度”，让模型能捕获不同模式的信息。文中的DeltaProduct可以视作这种思路的尝试。
  2. ​​高阶状态更新​​：探索超越一阶外积的更新方式。例如，是否可以引入一个低秩因子分解，用两个更小的矩阵 U_t 和 V_t 来更新状态，即 S_t = S_{t-1} + U_t V_t^T，其中 U_t 和 V_t 由当前输入计算得到。这可以在不显著增加计算量的前提下增加模型的灵活性。

3. 与先进位置编码的深度融合

• ​​当前局限​​：文章中提到PaTH Attention将DeltaNet的思想反哺到了Softmax Attention的位置编码中。这说明DeltaNet的数学形式本身蕴含着一种​​动态的、内容感知的位置信息​​。
• ​​改进方案​​：​​显式地将DeltaNet机制设计为一个独立的位置编码模块​​。例如：
  • 除了主导的DeltaNet层，许可并行维护一个专门用于生成位置偏置（Bias）的DeltaNet。这个“位置DeltaNet”的输入是某种形式的位置id嵌入，其输出的状态矩阵可以作为一种动态的ALiBi偏置，加到主Attention的分数上。
  • 这种改进不是直接修改DeltaNet的核心算法，而是将其作为一种强大的工具来增强整个模型架构，使其能更好地处理长度外推和感知位置信息。

4. 优化并行化实现与数值稳定性

• ​​当前局限​​：即使DeltaNet在理论上可以并行化（通过求解线性系统），但其高效实现非常复杂，依赖于精巧的数学变换和CUDA内核编程，如文中“求逆与推广”一节所述。这对于其广泛应用是一个障碍。
• ​​改进方案​​：
  1. ​​构建更简洁、更硬件友好的并行算法​​：寻找等价于DeltaRule的递推公式，使其能像Linear Attention或Chunkwise形式的SSM那样，用分块矩阵乘法高效实现，从而更好地利用GPU的Tensor Core。
  2. ​​数值稳定性​​：S_t = S_{t-1} (I - k_t k_t^T) + v_t k_t^T 中的 (I - k_t k_t^T) 项在数值上可能是不稳定的，尤其是在长期迭代后。研究如何通过数值分析技术（如重新正交化、更好的初始化）来保证训练和长序列推理时的稳定性是一个重要的工程改进点。

5. 探索超越平方损失的目标函数

• ​​当前局限​​：DeltaNet源于在线学习中对平方损失 ||S k_t - v_t||^2 的优化。平方损失假设误差服从高斯分布，但这对于复杂的Token间关系可能不是最优的。
• ​​改进方案​​：在TTT（Test Time Training）的框架下，​​探索其他损失函数​​。例如：
  • 使用​​Huber损失​​，它对异常值不如平方损失敏感，可能使训练更稳定。
  • 对于分类任务，可以探索基于​​对比学习​​的损失函数，让状态矩阵 S_t 不仅学会重建 v_t，还能拉近正确token表征间的距离，推远错误token间的距离。
  • 这相当于为DeltaNet设计一个新的“学习目标”，可能会带来性能的提升。

总结

改进方向	核心思想	潜在收益	主要挑战
​​材料依赖遗忘门​​	让模型根据输入动态决定遗忘和更新速率	提升模型灵活性，适应不同上下文	保持线性特性以实现并行化
​​增强状态表达能力​​	采用多头或更困难的因子化更新	提升参数效率和模型容量	控制计算复杂度
​​深度融合位置编码​​	将DeltaNet用作动态位置偏置生成器	改善长度外推和位置感知能力	模块设计的有效性
​​优化并行建立​​	开发分块矩阵乘法等硬件友好算法	降低实现门槛，提升训练/推理速度	算法的正确性与数值稳定性
​​探索新损失函数​​	在TTT框架下尝试Huber、对比损失等	可能获得更优的优化目标和性能	新损失函数的可导性和效果

DeltaNet是一个建立在坚实数学基础（在线学习）上的模型，其“除旧迎新”的机制非常优雅。上述改进方向旨在​​保留其核心优势的同时​​，在​​灵活性​​、​​表达能力​​、​​效率​​和​​稳定性​​等方面进行增强。其中，​​引入素材依赖的门控机制​​和​​优化其并行化搭建​最有 immediate value 的两个方向。就是​可能