03_01_SRBUCK传递函数推导

"花开你在"

SRBUCK传递函数推导[CCM]

对于BUCK变换器的基本分析我觉得这篇文章写得很好:
https://blog.csdn.net/weixin_42005993/article/details/120144144

buck电路拓扑如下:

1. LC低通滤波器传递函数推导

先看红线后面部分其实这就是一个LC低通滤波器的传递函数,但是还是来推导一遍

\(V_o=\frac{\frac{1}{sC}||R}{sL+\frac{1}{sC}||R}*V\)

\(\frac{1}{sC}||R = \frac{R}{1+sCR}\)

\(V_o = \frac{\frac{R}{1+sCR}}{\frac{sL(1+sCR)+R}{1+sCR}}*V\)

\(V_o = \frac{R}{s^2RLC+sL+R}*V\)

得到表达式1:

\(V_o=\frac{V}{LCs^2+\frac{L}{R}s+1}\)

2. 对于开关器件的处理

在理想情况下,一个周期内,Vi的平均值是不变的,V的平均值也是不变的
使用小信号进行分析加入扰动的情况:

\(V_i = \bar{V_i} + \hat{v_i}\)

\(V = \bar{V} + \hat{v}\)

\(D = \bar{D} + \hat{d}\)

显然有:\(\bar{V} + \hat{v} = (\bar{V_i} + \hat{v_i}) * (\bar{D} + \hat{d})\)

拆开则为:

\(\bar{V} + \hat{v} = \bar{V_i}*\bar{D} + \bar{V_i}*\hat{d} +\hat{v_i}*\bar{D}+\hat{v_i}*\hat{d}\), 其中(\(\bar{V}=\bar{V_i}*\bar{D}\))

因此化简得到:

\(\hat{v} = \bar{V_i}*\hat{d} +\hat{v_i}*\bar{D}\)

我们在处理的时候通常认为\(\hat{v_i}\)是不会变化的,因为理想化输入电压恒定
于是得到简介表达:

\(\hat{v} = \bar{V_i}*\hat{d}\)

将表达式1修改为小信号方程:

\(\hat{v_o}=\frac{\hat{v}}{LCs^2+\frac{L}{R}s+1}\)

于是得到:

\(\hat{v_o}=\frac{\bar{V_i}*\hat{d}}{LCs^2+\frac{L}{R}s+1}\)

最终得到了传递函数 :

\(G(s) = \frac{\hat{v_o}}{\hat{d}} = \frac{\bar{V_i}}{LCs^2+\frac{L}{R}s+1}\)

\(G(s) = \frac{\hat{v_o}}{\hat{d}} = \frac{V_i}{LCs^2+\frac{L}{R}s+1}\)

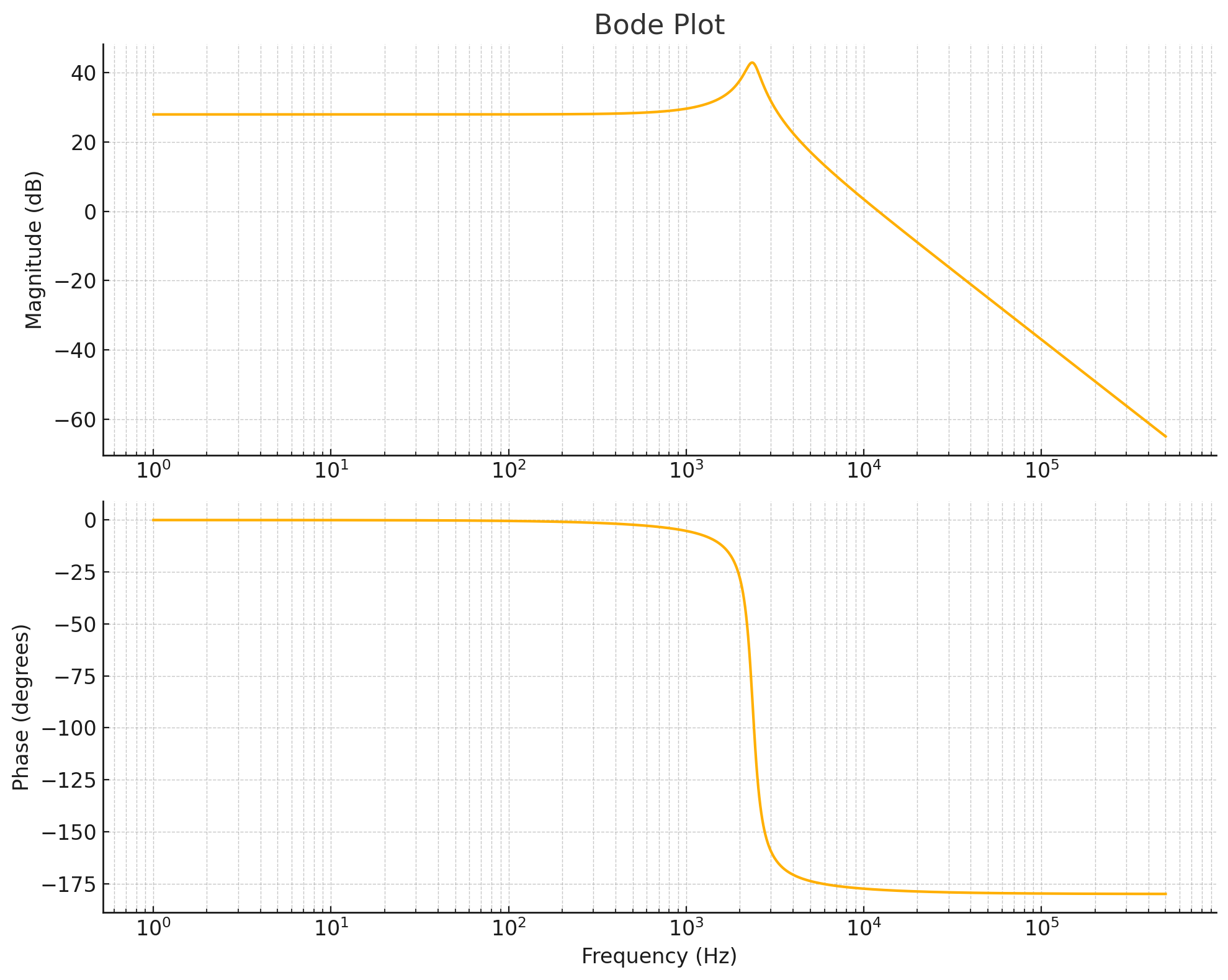
3. 波特图展示

既然好不容易得到了传递函数,这不得看一看?
假设一下参数:

vin = 25V

vo = 12V

Ro = 4Ω

L = 48uH

C = 2*47uF

因此得到传递函数为:

\[G(s) = \frac{25}{4.512 \times 10^{-9} s^2 + 1.2 \times 10^{-5} s + 1} \]

\[G(s) = \frac{5.54 \times 10^9}{s^2 + 2.66 \times 10^3 s + 2.216 \times 10^8} \]

波特图为: