势函数法

https://www.cnblogs.com/huadongw/p/4106290.html

 

势函数主要用于确定分类面，其思想来源于物理。

 

1 势函数法基本思想

• 假设要划分属于两种类别𝜔1ω1和𝜔2ω2的模式样本，这些样本可看成是分布在𝑛n维模式空间中的点𝑥𝑘xk。
• 把属于𝜔1ω1的点比拟为某种能源点，在点上，电位达到峰值。
• 随着与该点距离的增大，电位分布迅速减小，即把样本𝑥𝑘xk附近空间𝑥x点上的电位分布，看成是一个势函数𝐾(𝑥,𝑥𝑘)K(x,xk)。
• 对于属于𝜔1ω1的样本集群，其附近空间会形成一个"高地"，这些样本点所处的位置就是"山头"。
• 同理，用电位的几何分布来看待属于𝜔2ω2的模式样本，在其附近空间就形成"凹地"。
• 只要在两类电位分布之间选择合适的等高线，就可以认为是模式分类的判别函数。

 

2. 判别函数的产生

• 模式分类的判别函数可由分布在模式空间中的许多样本向量{𝑥𝑘,𝑘=1,2,⋯且,𝑥𝑘∈𝜔1∪𝑤2}{xk,k=1,2,⋯且,xk∈ω1∪w2}的势函数产生。
• 任意一个样本所产生的势函数以𝐾(𝑥,𝑥𝑘)K(x,xk)表征，则判别函数𝑑(𝑥)d(x)可由势函数序列𝐾(𝑥,𝑥1),𝐾(𝑥,𝑥2),⋯K(x,x1),K(x,x2),⋯来构成，序列中的这些势函数相应于在训练过程中输入机器的训练模式样本𝑥1,𝑥2,⋯x1,x2,⋯。
• 在训练状态，模式样本逐个输入分类器，分类器就连续计算相应的势函数，在第𝑘k步迭代时的积累位势决定于在该步前所有的单独势函数的累加。
• 以𝐾(𝑥)K(x)表示积累位势函数，若加入的训练样本𝑥𝑘+1xk+1是错误分类，则积累函数需要修改，若是正确分类，则不变。

 

3.判别函数产生逐步分析

    设初始势函数𝐾0(𝑥)=0K0(x)=0

    第一步：加入第一个训练样本𝑥1x1，

则有  

 

𝐾1(𝑥)={𝐾(𝑥,𝑥1)−𝐾(𝑥,𝑥1)if𝑥1∈𝜔1if𝑥1∈𝜔2K1(x)={K(x,x1)ifx1∈ω1−K(x,x1)ifx1∈ω2

 

这里第一步积累势函数𝐾1(𝑥)K1(x)描述了加入第一个样本时的边界划分。当样本属于𝜔1ω1时，势函数为正；当样本属于𝜔2ω2时，势函数为负。

      第二步：加入第二个训练样本𝑥2x2，

则有

1. 若𝑥2∈𝜔1x2∈ω1且𝐾1(𝑥2)>0K1(x2)>0，或𝑥2∈𝜔2x2∈ω2且𝐾1(𝑥2)<0K1(x2)<0，则分类正确，此时𝐾2(𝑥)=𝐾1(𝑥)K2(x)=K1(x)，即积累势函数不变。
2. 若𝑥2∈𝜔1x2∈ω1且𝐾1(𝑥——2)<0K1(x——2)<0，则
   𝐾2(𝑥)=𝐾1(𝑥)+𝐾(𝑥,𝑥2)=±𝐾(𝑥,𝑥1)+𝐾(𝑥,𝑥2)K2(x)=K1(x)+K(x,x2)=±K(x,x1)+K(x,x2)
3. 若𝑥2∈𝜔2x2∈ω2且𝐾1(𝑥2)>0K1(x2)>0，则

 

𝐾2(𝑥)=𝐾1(𝑥)−𝐾(𝑥,𝑥2)=±𝐾(𝑥,𝑥1)−𝐾(𝑥,𝑥2)K2(x)=K1(x)−K(x,x2)=±K(x,x1)−K(x,x2)

 

     以上（ii）、（iii）两种情况属于错分。假如𝑥2x2处于𝐾1(𝑥)K1(x)定义的边界的错误一侧，则当𝑥∈𝜔1x∈ω1时，积累位势𝐾2(𝑥)K2(x)要加𝐾(𝑥,𝑥2)K(x,x2)，当𝑥∈𝜔2x∈ω2时，积累位势𝐾2(𝑥)K2(x)要减𝐾(𝑥,𝑥2)K(x,x2)。

      第𝐾K步：设𝐾𝑘(𝑥)Kk(x)为加入训练样本𝑥1,𝑥2,⋯,𝑥𝑘x1,x2,⋯,xk后的积累位势，则加入第(𝑘+1)(k+1)个样本时，𝐾𝑘+1(𝑥)Kk+1(x)决定如下：

1. 若𝑥𝑘+1∈𝜔1xk+1∈ω1且𝐾𝑘(𝑥𝑘+1)>0Kk(xk+1)>0，或𝑥𝑘+1∈𝜔2xk+1∈ω2且𝐾𝑘(𝑥𝑘+1)<0Kk(xk+1)<0，则分类正确，此时𝐾𝑘+1(𝑥)=𝐾𝑘(𝑥)Kk+1(x)=Kk(x)，即积累位势不变。

2. 若𝑥𝑘+1∈𝜔1xk+1∈ω1且𝐾𝑘(𝑥𝑘+1)<0Kk(xk+1)<0，则𝐾𝑘+1(𝑥)=𝐾𝑘(𝑥)+𝐾(𝑥,𝑥𝑘+1)Kk+1(x)=Kk(x)+K(x,xk+1);

3. 若𝑥𝑘+1∈𝜔2xk+1∈ω2且𝐾𝑘(𝑥𝑘+1)>0Kk(xk+1)>0，则𝐾𝑘+1(𝑥)=𝐾𝑘(𝑥)−𝐾(𝑥,𝑥𝑘+1)Kk+1(x)=Kk(x)−K(x,xk+1).

     因此，积累位势的迭代运算可写成：𝐾𝑘+1(𝑥)=𝐾𝑘(𝑥)+𝑟𝑘+1𝐾(𝑥,𝑥𝑘+1)Kk+1(x)=Kk(x)+rk+1K(x,xk+1)，𝑟𝑘+1rk+1为校正系数：     

 

𝑟𝑘+1=⎧⎩⎨⎪⎪⎪⎪001−1𝑖𝑓𝑥𝑘+1∈𝜔1and𝐾𝑘(𝑥𝑘+1)>0𝑖𝑓𝑥𝑘+1∈𝜔2and𝐾𝑘(𝑥𝑘+1)<0𝑖𝑓𝑥𝑘+1∈𝜔1and𝐾𝑘(𝑥𝑘+1)<0𝑖𝑓𝑥𝑘+1∈𝜔2and𝐾𝑘(𝑥𝑘+1)>0rk+1={0ifxk+1∈ω1andKk(xk+1)>00ifxk+1∈ω2andKk(xk+1)<01ifxk+1∈ω1andKk(xk+1)<0−1ifxk+1∈ω2andKk(xk+1)>0

 

      若从给定的训练样本集𝑥1,𝑥2,⋯,𝑥𝑘,⋯x1,x2,⋯,xk,⋯中去除不使积累位势发生变化的样本，即使𝐾𝑗(𝑥𝑗+1)>0Kj(xj+1)>0且𝑥𝑗+1∈𝜔1xj+1∈ω1，或𝐾𝑗(𝑥𝑗+1)<0Kj(xj+1)<0且𝑥𝑗+1∈𝜔2xj+1∈ω2的那些样本，则可得一简化的样本序列{𝑥⌢1,𝑥⌢2,…,𝑥⌢𝑗,…}{x⌢1,x⌢2,…,x⌢j,…}，它们完全是校正错误的样本。此时，上述迭代公式可归纳为：

 

𝐾𝑘+1(𝑥)=∑𝑥⌢𝑗𝑎𝑗𝐾(𝑥,𝑥⌢𝑗)Kk+1(x)=∑x⌢jajK(x,x⌢j)

 

其中         

 

𝑎𝑗={+1−1𝑓𝑜𝑟𝑥⌢𝑗∈𝜔1𝑓𝑜𝑟𝑥⌢𝑗∈𝜔2aj={+1forx⌢j∈ω1−1forx⌢j∈ω2

 

也就是说，由𝑘+1k+1个训练样本产生的积累位势，等于𝜔1ω1类和𝜔2ω2类两者中的校正错误样本的总位势之差。

 

      从势函数可以看出，积累位势起着判别函数的作用：当𝑥𝑘+1xk+1属于𝜔1ω1时，𝐾𝑘(𝑥𝑘+1)>0Kk(xk+1)>0；当𝑥𝑘+1xk+1属于𝜔2ω2时，𝐾𝑘()𝑥𝑘+1<0Kk()xk+1<0，则积累位势不做任何修改就可用作判别函数。

由于一个模式样本的错误分类可造成积累位势在训练时的变化，因此势函数算法提供了确定𝜔1ω1和𝜔2ω2两类判别函数的迭代过程。判别函数表达式：取𝑑(𝑥)=𝐾(𝑥)d(x)=K(x)，则有：𝑑𝑘+1(𝑥)=𝑑𝑘(𝑥)+𝑟𝑘+1𝐾(𝑥,𝑥𝑘+1)dk+1(x)=dk(x)+rk+1K(x,xk+1).

 

4 构成势函数的两种方式：

    第一类势函数和第二类势函数 

     第一类势函数：

     可用对称的有限多项式展开，即：

 

𝐾(𝑥,𝑥𝑘)=∑𝑖=1𝑚𝜙𝑖(𝑥)𝜙𝑖(𝑥𝑘)K(x,xk)=∑i=1mϕi(x)ϕi(xk)

 

其中{}在模式定义域内为正交函数集。将这类势函数代入判别函数，有：

 

𝑑𝑘+1(𝑥)=𝑑𝑘(𝑥)+𝑟𝑘+1∑𝑖=1𝑚𝜙𝑖(𝑥𝑘+1)𝜙𝑖(𝑥)=𝑑𝑘(𝑥)+∑𝑖=1𝑚𝑟𝑘+1𝜙𝑖(𝑥𝑘+1)𝜙𝑖(𝑥)dk+1(x)=dk(x)+rk+1∑i=1mϕi(xk+1)ϕi(x)=dk(x)+∑i=1mrk+1ϕi(xk+1)ϕi(x)

 

得迭代关系：

 

𝑑𝑘+1(𝑥)=∑𝑖=1𝑚𝐶𝑖(𝑘+1)𝜙𝑖(𝑥)dk+1(x)=∑i=1mCi(k+1)ϕi(x)

 

其中

 

𝐶𝑖(𝑘+1)=𝐶𝑖(𝑘)+𝑟𝑘+1𝜙𝑖(𝑥𝑘+1)Ci(k+1)=Ci(k)+rk+1ϕi(xk+1)

 

因此，积累位势可写成：

 

𝐾𝑘+1(𝑥)=∑𝑖=1𝑚𝐶𝑖(𝑘+1)𝜙𝑖(𝑥)Kk+1(x)=∑i=1mCi(k+1)ϕi(x)

 

$C_i$可用迭代式求得。 

     第二类势函数：

     选择双变量𝑥x和$x_k_$的对称函数作为势函数，即$K(x, x_k) = K(x_k, x)$，并且它可展开成无穷级数，例如：

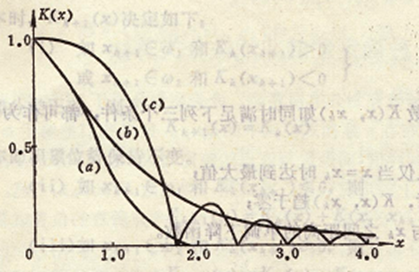
(a)  𝐾(𝑥,𝑥𝑘)=𝑒−𝛼‖𝑥−𝑥𝑘‖2K(x,xk)=e−α‖x−xk‖2

(b)  𝐾(𝑥,𝑥𝑘)=11+𝛼‖𝑥−𝑥𝑘‖2K(x,xk)=11+α‖x−xk‖2, 𝛼α是正常数

(c)  𝐾(𝑥,𝑥𝑘)=∣∣∣sin𝛼‖𝑥−𝑥𝑘‖2𝛼‖𝑥−𝑥𝑘‖2∣∣∣K(x,xk)=|sin⁡α‖x−xk‖2α‖x−xk‖2|

 

5.势函数法

实例1：用第一类势函数的算法进行分类

1. 选择合适的正交函数集{}

选择Hermite多项式，其正交域为(-∞, +∞)，其一维形式是

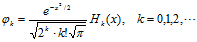
其正交性：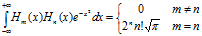

其中，H_k(x)前面的乘式为正交归一化因子，为计算简便可省略。因此，Hermite多项式前面几项的表达式为

H₀(x)=1,        H₁(x)=2x,        H₂(x)=4x²-2,

H₃(x)=8x³-12x,        H₄(x)=16x⁴-48x²+12

1. 建立二维的正交函数集

二维的正交函数集可由任意一对一维的正交函数组成，这里取四项最低阶的二维的正交函数

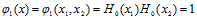
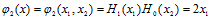
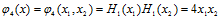
1. 生成势函数

按第一类势函数定义，得到势函数

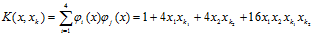
其中，

1. 通过训练样本逐步计算累积位势K(x)

给定训练样本：ω₁类为x_①=(1 0)^T, x_②=(0 -1)^T

ω₂类为x_③=(-1 0)^T, x_④=(0 1)^T

累积位势K(x)的迭代算法如下

第一步：取x_①=(1 0)^T∈ω₁，故

K₁(x)=K(x, x_①)=1+4x₁·1+4x₂·0+16x₁x₂·1·0=1+4x₁

第二步：取x_②=(0 -1)^T∈ω₁，故K₁(x_②)=1+4·0=1

因K₁(x_②)>0且x_②∈ω₁，故K₂(x)=K₁(x)=1+4x₁

第三步：取x_③=(-1 0)^T∈ω₂，故K₂(x_③)=1+4·(-1)=-3

因K₂(x_③)<0且x_③∈ω₂，故K₃(x)=K₂(x)=1+4x₁

第四步：取x_④=(0 1)^T∈ω₂，故K₃(x_④)=1+4·0=1

因K₃(x_④)>0且x_④∈ω₂，

故K₄(x)=K₃(x)-K(x,x_④)=1+4x₁-(1+4x₂)=4x₁-4x₂

将全部训练样本重复迭代一次，得

第五步：取x_⑤=x_①=(1 0)^T∈ω₁，K₄(x_⑤)=4

故K₅(x)=K₄(x)=4x₁-4x₂

第六步：取x_⑥=x_②=(0 -1)^T∈ω₁，K₅(x_⑥)=4

故K₆(x)=K₅(x)=4x₁-4x₂

第七步：取x_⑦=x_③=(-1 0)^T∈ω₂，K₆(x_⑦)=-4

故K₇(x)=K₆(x)=4x₁-4x₂

第八步：取x_⑧=x_④=(0 1)^T∈ω₂，K₇(x_⑧)=-4

故K₈(x)=K₇(x)=4x₁-4x₂

以上对全部训练样本都能正确分类，因此算法收敛于判别函数

d(x)= 4x₁-4x₂

 

实例2：用第二类势函数的算法进行分类

 

 

选择指数型势函数，取α=1，在二维情况下势函数为

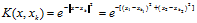
这里：ω₁类为x_①=(0 0)^T, x_②=(2 0)^T

ω₂类为x_③=(1 1)^T, x_④=(1 -1)^T

可以看出，这两类模式是线性不可分的。算法步骤如下：

第一步：取x_①=(0 0)^T∈ω₁，则

K₁(x)=K(x,x_①)=

第二步：取x_②=(2 0)^T∈ω₁

因K₁(x_②)=e^-(4+0)=e^-4>0，

故K₂(x)=K₁(x)=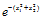

第三步：取x_③=(1 1)^T∈ω₂

因K₂(x_③)=e^-(1+1)=e^-2>0，

故K₃(x)=K₂(x)-K(x,x_③)=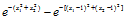

第四步：取x_④=(1 -1)^T∈ω₂

因K₃(x_④) =e^-(1+1)-e^-(0+4)=e^-2-e^-4>0，

故K₄(x)=K₃(x)-K(x,x_④)

=

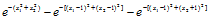
需对全部训练样本重复迭代一次

第五步：取x_⑤=x_①=(0 0)^T∈ω₁，K₄(x_⑤)=e⁰-e^-2-e^-2=1-2e^-2>0

故K₅(x)=K₄(x)

第六步：取x_⑥=x_②=(2 0)^T∈ω₁，K₅(x_⑥)=e^-4-e^-2-e^-2=e^-4-2e^-2<0

故K₆(x)=K₅(x)+K(x,x_⑥)

=

第七步：取x_⑦=x_③=(1 1)^T∈ω₂，K₆(x_⑦)=e^-2-e⁰-e^-4+e^-2=2e^-2-e^-4-1<0

故K₇(x)=K₆(x)

第八步：取x_⑧=x_④=(1 -1)^T∈ω₂，K₇(x_⑧)=e^-2-e^-4-e⁰+e^-2=2e^-2-e^-4-1<0

故K₈(x)=K₇(x)

第九步：取x_⑨=x_①=(0 0)^T∈ω₁，K₈(x_⑨)=e⁰-e^-2-e^-2+e^-4=1+e^-4-2e^-2>0

故K₉(x)=K₈(x)

第十步：取x_⑩=x_②=(2 0)^T∈ω₁，K₉(x_⑩)=e^-4-e^-2-e^-2+e⁰=1+e^-4-2e^-2>0

故K₁₀(x)=K₉(x)

经过上述迭代，全部模式都已正确分类，因此算法收敛于判别函数

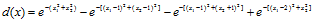
势函数分类算法评价：

1.用第二类势函数，当训练样本维数和数目都较高时，需要计算和存储的指数项较多。

2. 正因为势函数由许多新项组成，因此有很强的分类能力。势函数法