斜率优化学习笔记

下面可能会用到一些叫上凸壳鸭下凸壳呀的名词，大家不用弄懂它的概念的说也不用望风而逃（我之前就望风而逃过(*/ω＼*)），凸壳就简单理解成一个凸了一块的一段连线就好了。

斜率优化有些地方不好用代数的语言刻画，比如下凸壳，比如凸包（凸包有的定义就直接写橡皮筋的比喻 233333），以及为什么下凸点/上凸点不可能是最优决策，还有线性规划的选点，但是我们画个图就容易感知，所以大家多画画图就好了（(/ω＼)）

战术分析

我们先来看一个简单的 dp 方程，\(f(i) = \max\{f(j) + A(i)B(j)\}\) 其中 \(A(i),B(j)\) 分别为关于 \(i\) 和 \(j\) 的某个多项式。这里我们就不能用单调队列优化的技巧了，因为没法分离这几项，所以我们必须用一些奇技淫巧。

我们拆掉 \(max\) 变成 \(f(i) = f(j) + A(i)B(j)\)，移一个项变成 \(-A(i)B(j) + f(i) = f(j)\)。如果你一次函数学的够好，对于一个一次函数的标准形式 \(y = kx+b\)，我们发现这个形式和刚刚的式子很像——\(k = -A(i), b = f(i), y = f(j)\)，那么问题就变成了——

平面直角坐标系上有很多个点 \((B(j), f(j))\)，现在有一个斜率为 \(-A(i)\) 的直线在上下平移，现在希望这个直线的截距尽量大，问你可以取到哪个点。

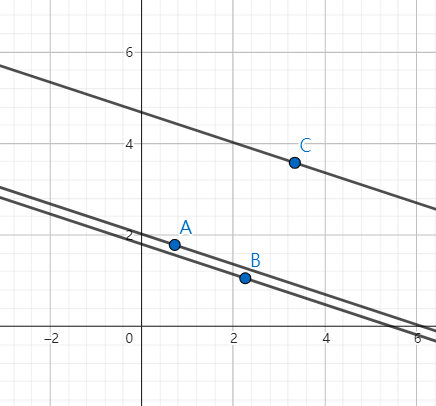
我们来战术分析一下，尽可能排除不可能决策。我们默认 \(A(i)\) 为正数（直线下降）。然后我们来看这样一张图——

这里面 ABC 三个点其中 B 点下凸了，用非常厉害的很专业的话来说，这叫“下凸壳的一部分”。我们会发现其中下凸的 B 点永远也不可能是答案，从图上可以直观的感受出来。

从而可以得到这样一个结论

1. 对于一段下凸壳，除了边缘两个点（因为从这两个点出发往上还有一个上凸壳，这两点也在上凸壳里面），其它点都不可能是最优决策。
2. 对于一段上凸壳，所有点（包括边缘两个也在下凸壳内的点）都有可能是最优决策。

这启发我们维护上凸壳，但是假设我很毒瘤我所有点都在上凸壳上我还是得 \(O(n^2)\) 慢跑，所以我们现在要解决两个问题

1. 如何合理运用上凸壳信息。
2. 如何快速维护一个上凸壳。

如果你学过线性规划有关知识的话，你会知道上凸壳上所有点的斜率都是递减的，对于一条斜率为 \(k\) 的直线，我们只要找到之前所有点斜率都大于等于它，之后所有点斜率都小于等于它的那个点就可以了。我们完全可以二分。

对于第二个问题，一般来讲我们的 \(B(j)\) 是一个单调不减的，所以我们每次加入的点必然在凸包上。我们维护一个单调栈（单调的是里面斜率递减），然后每次新加一个点，看看最后两个点的斜率是否大于最后一个点和新点的斜率，如果大于那么就一直弹出栈顶元素。

---

总结

最后我们总结一下斜率优化。

其实斜率优化的一般形式是 \(f(i) = \max\{f(j) + A(i)B(j)+ C(i)+D(j)\}\)，其中 \(A,B,C,D\) 均为只与 \(i\) 有关或 \(j\) 有关的多项式。

对于取 \(max\) 的流程是——

1. 把 \(max\) 去掉，变成 \(f(i) = f(j)+A(i)B(j)+C(i)+D(j)\)。
2. \(C(i)\) 看成常数，然后把它遮住，\(f(i)' = f(j) + A(i)B(j) +D(j)\)
3. 移项得到 \(-A(i)B(j) + f(i)' = f(j) + D(j)\)。
4. 用单调栈维护一个上凸壳，里面的点是 \((B(j), f(j) + D(j))\)，二分出一个 \(k\) 满足上凸壳之前的点斜率都大于等于它，之后的斜率都小于等于 \(-A(i)\)，这就是我们要找的 \(j\)。
5. 转移。
6. 每次比较单调栈内最后两个点和最后一个点与新的点的斜率，如果旧斜率小于新斜率就弹出旧斜率。

对于取 \(min\) 的流程是——

1. 把 \(min\) 去掉，变成 \(f(i) = f(j)+A(i)B(j)+C(i)+D(j)\)。
2. \(C(i)\) 看成常数，然后把它遮住，\(f(i)' = f(j) + A(i)B(j) +D(j)\)
3. 移项得到 \(-A(i)B(j) + f(i)' = f(j) + D(j)\)。
4. 用单调栈维护一个下凸壳，里面的点是 \((B(j), f(j) + D(j))\)，二分出一个 \(k\) 满足上凸壳之前的点斜率都小于等于它，之后的斜率都大于等于 \(-A(i)\)，这就是我们要找的 \(j\)。
5. 转移。
6. 每次比较单调栈内最后两个点和最后一个点与新的点的斜率，如果旧斜率大于新斜率就弹出旧斜率。

---

关于决策单调性

对于取 \(max\)，如果 \(-A(i)\) 单调不升（\(A(i)\) 单调不降），那么我们二分出来的 \(k\) 是单调不减的（决策单调性），我们就可以用一个双端队列维护，队头是决策，队尾是弹出来的。维护的话就是把上面的第 4 步改成 队头和第二个元素的斜率如果大于 \(-A(i)\) 就弹出队头（因为它们永远也用不上。）
取 \(min\)，同理，如果 \(-A(i)\) 单调不降（\(A(i)\) 单调不升），那么我们二分出来的 \(k\) 也是单调不减的的，所以我们也可以用双端队列，第 4 步改成队头和第二个元素的斜率如果小于 \(-A(i)\) 就弹出队头。

---

题目

P3195

典题，设 \(f(i)\) 代表前 \(i\) 个玩具装箱的最小代价，\(sum(i) = \sum\limits_{j = 1}^{i}(C_j + 1)\)，加一是为了直接消掉 \(i - j\)，但是此时我 \(sum(r) - sum(l - 1) = r - l + 1 - \sum\limits_{j = l}^rC_j\)，还多了一个 \(1\)，把 \(l = L+1\)，就行了，方程就是 \(f(i) = \min\{f(j) + (sum(i) - sum(j) - l)^2\}\)

感觉这个前缀和和 \(l\) 加一很巧妙鸭，虽然也可以不这样，但是如果直接做拆项是一件很痛苦的事情，现在这样大大简化了，毕竟三项式平方很好拆。这个平方长得很斜率优化，我们就把 \(min\) 擦掉，然后战术展开

\(f(i) = f(j) + sum(i)^2+sum(j)^2+l^2-2sum(i)l-2sum(i)sum(j) +2sum(j)l\)。\(i,l\) 看成定值，所以 \(C(i) = sum(i)^2+l^2-2sum(i)l\) 可看成常数。只和 \(j\) 有关的项也领出来，\(D(j) = f(j) + 2sum(j)l +sum(j)^2\)（这里和上面有个小小的出入，就是直接把 \(f(j)\) 放到函数里面，不过都一个意思）方程被化简为 \(f(i) = C(i) + D(j) - 2sum(i)sum(j)\)。

这是一个标准的斜率优化，斜率是 \(-2sum(i)\)，相反数 \(2sum(i)\) 单调不降，所以它有决策单调性，我们用双端队列维护，时间复杂度 \(O(n)\)。

请注意一下里面是取等号还是小于还是大于，并且这道题为了方便我是用 double 存斜率，但是实际上我们应该用乘法，因为 double 会掉精度

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 5e4;
int n;
ll L, a[MAXN + 10], sum[MAXN + 10], f[MAXN + 10];

struct node {
	ll x, y;
};
double xielv(node n1, node n2) {
	ll X1 = n1.x, Y1 = n1.y, X2 = n2.x, Y2 = n2.y;
	return ((double)(Y2 - Y1) / (double)(X2 -  X1));
}

node que[MAXN + 10];//tu ke
int head = 1, tail = 0;
void pop_front() {head++;}
void pop_back() {tail--;}
void add_back(ll X, ll Y) {
	que[++tail].x = X;
	que[tail].y = Y;
}
int size() {return tail - head + 1;}

ll A(ll j) {return f[j] + sum[j] * sum[j] + 2 * sum[j] * L;}
ll C(ll i) {return sum[i] * sum[i] + L * L - 2 * sum[i] * L;}
void init() {
	memset(f, 0x3f, sizeof(f));
	cin >> n >> L;
	for(int p = 1; p <= n; p++)
		cin >> a[p], sum[p] = sum[p - 1] + a[p] + 1;
	L++;

	f[0] = 0;
	add_back(0, 0);
	for(int i = 1; i <= n; i++) {
		while(size() >= 2 && xielv(que[head], que[head + 1]) < double(2ll * sum[i])) pop_front();
		f[i] = min(f[i], que[head].y - 2ll * sum[i] * que[head].x + C(i));
		node qwq; qwq.x = sum[i], qwq.y = A(i);
		while(size() >= 2 && xielv(que[tail], que[tail - 1]) >= xielv(que[tail], qwq)) pop_back();
		add_back(qwq.x, qwq.y);
	}
	cout << f[n] << endl;
}
int main() {
	init();
}