马尔可夫链蒙特卡罗算法（MCMC）

文章结构如下：

1: MCMC

1.1 MCMC是什么
1.2 为什么需要MCMC

2：蒙特卡罗

2.1 引入
2.2 均匀分布，Box-Muller 变换
2.3 拒绝接受采样（Acceptance-Rejection Sampling）
2.4 接受拒绝采样的直观解释
2.5 接受拒绝采样方法有效性证明
2.6 接受拒绝采样方法python实现
2.7 蒙特卡罗方法小结

3：马尔科夫链

3.1 马尔科夫链概述
3.2 马尔科夫链模型状态转移矩阵的性质
3.3 基于马尔科夫链采样
3.4 马尔科夫链采样小结
3.5 补充：PageRank：Google的民主表决式网页排名技术

4：马尔可夫链蒙特卡罗算法

4.1 马尔科夫链的细致平稳条件(Detailed Balance Condition)
4.2 MCMC采样

5： M-H采样

5.1 M-H采样算法
5.2 M-H采样python实现
5.3 M-H采样小结

6：Gibbs采样

6.1 重新寻找合适的细致平稳条件
6.2 二维Gibbs采样
6.3 多维Gibbs采样
6.4 二维Gibbs采样python实现
6.5 Gibbs采样小结

7：参考文献

不喜欢数学推导的可以移至这么篇文章：告别数学公式，图文解读什么是马尔可夫链蒙特卡罗方法（MCMC），这篇文章通俗的解释了MCMC是什么，本文也借鉴了里面一些内容。本文主要参考的刘建平博客：MCMC 。其他参考文章也在文末附上。另外大牛的文章也到单独附上，刘建平主要参考了此文章：靳志辉写的：LDA-math-MCMC 和 Gibbs Sampling ，PDF是《LDA数学八卦》，现在离开腾讯出来创业了，第一次知道他还是看了《正态分布的前世今生》。反正大神！

1: MCMC

1.1. MCMC是什么

那MCMC到底是什么呢？《告别数学公式，图文解读什么是马尔可夫链蒙特卡罗方法》里面这样解释：MCMC方法是用来在概率空间，通过随机采样估算兴趣参数的后验分布。

说的很玄，蒙特卡罗本来就可以采样，马尔科夫链可以采样，为啥要将他们合在一起？下面给出两个动机，后面将从蒙特卡罗开始一直推到gibbs采样，来深入了解为什么需要MCMC。

再次感谢刘建平MCMC，他是网上写的最详细的——将整个脉络梳理出来了，看完收获很多。本文几乎涵盖了它所有内容，因此只能算一篇读书笔记。

1.2：为什么需要MCMC

动机一

假如你需要对一维随机变量$X$进行采样， $X$ 的样本空间是 $\{1,2,3\}$ ，且概率分别是 $\{1/2,1/4,1/4\}$ ，这很简单，只需写这样简单的程序：首先根据各离散取值的概率大小对 $[0,1]$ 区间进行等比例划分，如划分为 $[0,0.5],[0,5,0.75],[0.75,1]$ 这三个区间，再通过计算机产生 $[0,1]$ 之间的伪随机数，根据伪随机数的落点即可完成一次采样。接下来，假如 $X$ 是连续分布的呢，概率密度是 $f(X)$ ，那该如何进行采样呢？聪明的你肯定会想到累积分布函数， $P(X<t)=\int _{-\infty}^{t}f(x)dx$ ，即在 $[0,1]$ 间随机生成一个数 $a$ ，然后求使得使 $P(x<t)=a$ 成立的 $t$ ， $t$ 即可以视作从该分部中得到的一个采样结果。这里有两个前提：一是概率密度函数可积；第二个是累积分布函数有反函数。假如条件不成立怎么办呢？MCMC就登场了。

动机二

假如对于高维随机变量，比如 $\mathbb{R}^{50}$ ，若每一维取100个点，则总共要取 $10^{100}$ ，而已知宇宙的基本粒子大约有 $10^{87}$ 个，对连续的也同样如此。因此MCMC可以解决“维数灾难”问题。

2：蒙特卡罗

2.1 引入

蒙特卡罗方法于20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”计划时首先提出，为保密选择用赌城摩纳哥的Monte Carlo作为代号。

对于上图你如何求解圆的面积？当然知道圆的直径，或根据圆的方程进行积分很容易求解。也可以用如下方法进行简单近似：

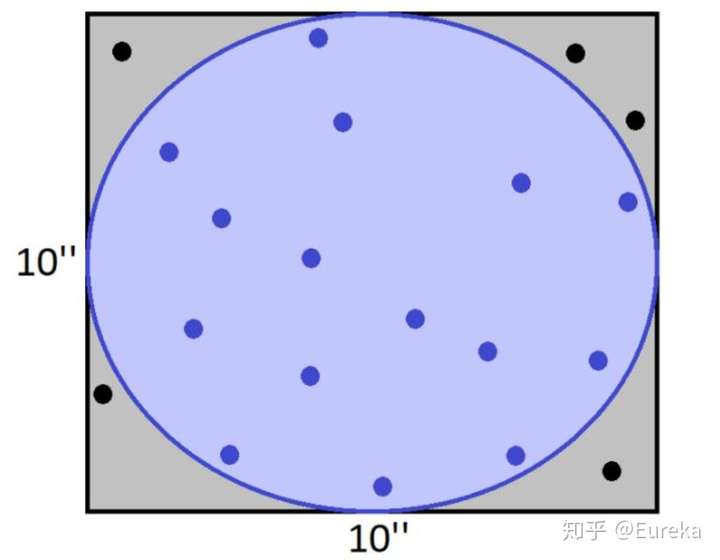
我们可以在这个正方形内随机撒20个米粒，然后我们数一下有多少个米粒落在圆圈内，计算这部分比例，并乘以正方形的面积。如上图大概是3/4正方形的面积。

这个方法在我们无法知道形状的方程时很有用，如下图的蝙蝠：

在一块长方形区域内随机抛掷点，蒙特卡罗方法能非常轻松地计算出该区域的近似值。

其上等价于如下公式：面积= $\int _{a}^{b}f(x)dx=\frac{b-a}{n}\sum_{i=1}^{n}f(x_{i})$ ，即求出高度的均值在乘以宽度，因为任何一个不规则图形的面积都等价于一个矩形的面积。

但是它隐含了一个假定，即 $x$ 在 $[a,b]$ 之间是均匀分布的，而绝大部分情况， $x$ 在 $[a,b]$ 之间不是均匀分布的。我们可以如下表示： $\int _{a}^{b}\frac{f(x)}{q(x)}q(x)dx$

这里把 $q(x)$ 看做是 $x$ 在区间内的概率分布函数，而把前面的分数部分看做一个函数，然后在 $q(x)$ 下抽取 $n$ 个样本，当 $n$ 足够大时，可以用采用均值来近似： $\sum_{i=1}^{n}\frac{f(x)}{q(x)}$ ，这个形式就是蒙特卡罗方法的一般形式。

2.2 均匀分布，Box-Muller 变换

均匀分布是很容易采样的，比如在计算机中生成 $[0,1]$ 之间的伪随机数序列，就可以看成是一种均匀分布。而我们常见的概率分布，无论是连续的还是离散的分布，都可以基于 $Uniform(0,1)$ 的样本生成。例如正态分布可以通过著名的Box−Muller变换得到:

Box-Muller 变换

如果随机变量 $U_{1},U_{2}$ 独立且 $U_{1},U_{2}\sim Uniform[0,1]$ ，

$Z_{0}=\sqrt{-2ln~U_{1}}cos(2\pi U_{2})\\$

$Z_{1}=\sqrt{-2ln~U_{1}}sin(2\pi U_{2})\\$

则 $Z_{0},Z_{1}$ 独立且服从标准正态分布。

其它几个著名的连续分布，包括指数分布、Gamma 分布、t 分布、F 分布、Beta 分布、Dirichlet 分布等等,也都可以通过类似的数学变换得到；离散的分布通过均匀分布更加容易生成。在python的numpy，scikit-learn等类库中，都有生成这些常用分布样本的函数可以使用。

不过当 $p(x)$ 的形式很复杂，或者 $p(\mathbf{x})$ 是个高维的分布的时候，样本的生成就可能很困难了。譬如有如下的情况:

1) $p(x)=\frac{\tilde{p}(x)}{\int \tilde{p}(x)dx}$ ， $\tilde{p}(x)$ 我们可以得到，但是下面的积分我们无法得到显示解（归一化系数很难计算）；

2) $p(x,y)$ 是一个二维的分布函数，这个函数本身计算很困难，但是条件分布 $p(x|y),p(y|x)$ 的计算相对简单; 如果 $p(\mathbf{x})$ 是高维的，这种情形就更加明显。

2.3 拒绝接受采样（Acceptance-Rejection Sampling）

需求：根某已知分布的概率密度函数 $f(x)$ ，产生服从此分布的样本 $X$
准备工作：

需要一个辅助的“建议分布proposal distribution” $G$ （已知其概率密度函数 $g(y)$ ）来产生候选样本。——由分布来产生候选样本，因此需要我们能够从 $G$ 抽样。即我们必须能够生成服从此概率分布的样本 $Y$ 。比如可以选择均匀分布、正态分布。
还需要另一个辅助的均匀分布 $U(0,1)$ 。
计算一个常数值 $c$ 。——满足不等式 $c∗g(x)\geqslant f(x)$ 的最小值 $c$ （当然，我们非常希望 $c$ 接近于1)

3. 开始样本生成：

从建议分布 $G$ 抽样，得到样本 $Y$ 。
从分布 $U(0,1)$ 抽样，得到样本 $U$ 。
如果 $U\leqslant\frac{f(Y)}{c*g(Y)}$ ，则令 $X=Y$ （接受 $Y$ ），否则继续执行步骤1（拒绝）。

2.4 接受拒绝采样的直观解释

假设使用 $U(0,1)$ 来作为“proposal distribution” $G$ ，这样 $g(x)=1\forall x\in [0,1]$ 。如下图所示，我们每次生成的两个样本 $Y$ 与 $U$ ，对应下图中矩形内的一点 $P(Y,U∗c∗g(Y))$ 。接受条件 $U\leqslant f(Y)c∗g(Y)$ ，即 $U∗c∗g(Y)\leqslant f(Y)$ 的几何意义是点 $P$ 在 $f(x)$ 下方，不接受 $Y$ 的几何意义是点 $P$ 在 $f(x)$ 的上方。在 $f(x)$ 下方的点(o形状)满足接受条件，上方的点(+形状)不满足接受条件。

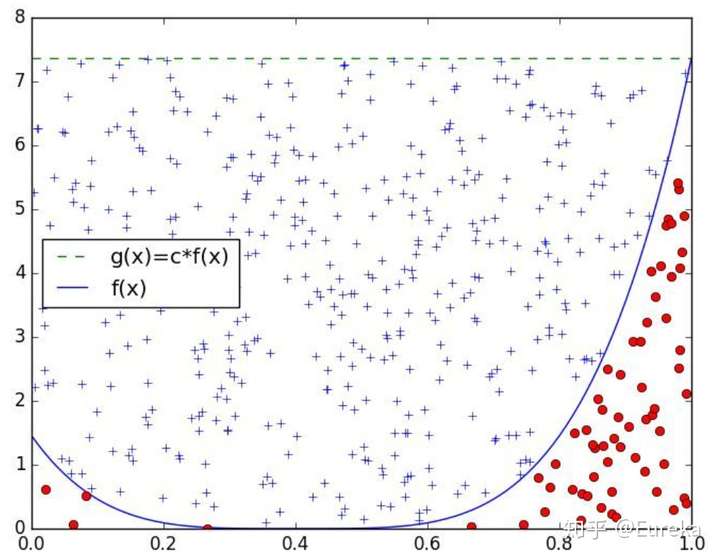
2.5 接受拒绝采样方法有效性证明

在我们进行证明之前，先给出几个非常重要的性质：

$f(Y)$ 和 $g(Y)$ 是随机变量，因此在第三步中 $\frac{f(Y)}{c*g(Y)}$ 和 $U$ 是独立的。
$0<\frac{f(Y)}{c*g(Y)}\leqslant 1$
从proposal分布和均匀分布中成功一次获得 $X$ 的抽样（迭代）次数 $N$ 也是个随机变量，服从概率是 $p=P(U\leqslant\frac{f(Y)}{c*g(Y)}$ 的几何分布： $P(N=n)=(1-p)^{n-1}p,n\geqslant1$ ，因此成功一次获得 $X$ 的平均抽样（迭代）次数是 $E(N)=1/p$
最后我们获得 $X$ 在 $Y$ 给定下的条件分布，即 $\{U\leqslant\frac{f(Y)}{c*g(Y)}\}$ 成立

我们可以直接计算出 $p=1/c$ ，因为 $P(U\leqslant\frac{f(Y)}{c*g(Y)}|Y=y)=\frac{f(Y)}{c*g(Y)}$

求积分得：

$p=\int _{-\infty}^{\infty}\frac{f(Y)}{c*g(Y)}\times g(y)dy\\$

$\frac{1}{c}\int _{-\infty}^{\infty}f(Y)dy=\frac{1}{c}\\$

因此 $E(N)=c$ ，从而得到我们选择一个 $g$ 函数从而使 $c$ 最小的合理性。

下面证明接受拒绝采样的有效性：

我们需要证明的是： $P(Y\leqslant y|U\leqslant\frac{f(Y)}{c*g(Y)})=F(y)$ 。我们定义： $B=\{U\leqslant\frac{f(Y)}{c*g(Y)}\}$ , $A=\{Y\leqslant y\}$ 。从上面我们知道： $P(B)=p=1/c$ ，然后我们使用贝叶斯： $P(A|B)=P(B|A)P(A)/P(B)$ 可以得到：

$P(Y\leqslant y|U\leqslant\frac{f(Y)}{c*g(Y)})=P(U\leqslant\frac{f(Y)}{c*g(Y)}|Y\leqslant y)\times \frac{G(y)}{1/c}=\frac{F(y)}{cG(y)}\times \frac{G(y)}{1/c}=F(y)$

其中： $P(U\leqslant\frac{f(Y)}{c*g(Y)}|Y\leqslant y)=\frac{P(U\leqslant\frac{f(Y)}{c*g(Y)},Y\leqslant y)}{G(y)}=\int _{-\infty}^{y}\frac{P(U\leqslant\frac{f(Y)}{c*g(Y)}|Y=\omega \leqslant y)}{G(y)}g(\omega )d\omega$ $=\frac{1}{G(y)}\int _{-\infty}^{y}\frac{f(\omega)}{cg(\omega)}g(\omega)d\omega=\frac{1}{cG(y)}\int _{-\infty}^{y}f(\omega)d\omega=\frac{F(y)}{cG(y)}$

2.6 python实现

假如我们的目标概率密度函数是 $f(x)=\frac{(x-0.4)^{4}}{\int_{0}^{1}(x-0.4)^{4}dx}$ ，对此分布生成样本。

准备工作：

建议分布函数 $G$ 选择 $U(0,1)$ ，概率密度函数为 $g(x)=1\forall x\in [0,1]$ 。（这里我们简单化了，一般要使得c最小的g函数）;
辅助的均匀分布 $U(0,1)$ ;
计算常数值， $c=max\{0.4^{4}/sum,0.6^{4}/sum\}=0.6^{4}/sum$ ,（其中 $sum=\int_{0}^{1}(x-0.4)^{4}dx$ ，后面可以化简掉）

2. 生成代码如下：

import random
import math
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

%matplotlib inline
sns.set_style('darkgrid')
plt.rcParams['figure.figsize'] = (12, 8)


def AceeptReject(split_val):
    global c
    global power
    while True:
        x = random.uniform(0, 1)
        y = random.uniform(0, 1)
        if y*c <= math.pow(x - split_val, power):
            return x

power = 4
t = 0.4  
sum_ = (math.pow(1-t, power + 1) - math.pow(-t, power + 1)) / (power + 1)  #求积分
x = np.linspace(0, 1, 100)
#常数值c
c = 0.6**4/sum_
cc = [c for xi in x]
plt.plot(x, cc, '--',label='c*f(x)')
#目标概率密度函数的值f(x)
y = [math.pow(xi - t, power)/sum_ for xi in x]
plt.plot(x, y,label='f(x)')
#采样10000个点
samples = []
for  i in range(10000):
    samples.append(AceeptReject(t))
plt.hist(samples, bins=50, normed=True,label='sampling')
plt.legend()
plt.show()

2.7 蒙特卡罗方法小结

使用接受-拒绝采样，我们可以解决一些概率分布不是常见的分布的时候，得到其采样集并用蒙特卡罗方法求和得到。但是接受-拒绝采样也只能部分满足我们的需求，在很多时候我们还是很难得到我们的概率分布的样本集。比如之前的第一个问题有时可以解决，但又会产生另一个问题：

对于一些二维分布 $p(x,y)$ ，我们只能得到条件分布 $p(x|y),p(y|x)$ ，却不能得到二维分布的一般形式；
对于复杂非常见分布 $p(x_{1},x_{2},...,x_{n})$ ，我们很难找到合适的 $q(x),c$ 。

要想将蒙特卡罗方法作为一个通用的采样模拟求和的方法，还的需马尔科夫链的帮忙。

3 马尔科夫链

3.1 马尔科夫链概述

马尔科夫链定义本身比较简单，它假设某一时刻状态转移的概率只依赖于它的前一个状态。即 $P(X^{t+1}|X^{1},...,X^{t})=P(X^{t+1}|X^{t})$ 。

因为某一时刻状态转移只依赖于它的前一个状态，那么我们只要能求出系统中任意两个状态之间的转换概率，最终可得到状态转移概率矩阵。如下图孩子的心情的转变，转移概率矩阵为 $P=\begin{bmatrix}0.6 & 0.2 &0.2 \\ 0.3 & 0.4 &0.3 \\ 0 & 0.3 & 0.7\end{bmatrix}$ 。

3.2 马尔科夫链模型状态转移矩阵的性质

若假设初始的三个概率分别是 $[0.5,0.3,0.2]$ ，即 $t_{0}$ 时刻，50%概率是Cheerful，30%概率是So-so，20%概率是Sad，将此代入转移概率，我们一直计算到 $t_{100}$ 看看是什么情况：

transfer_matrix = np.array([[0.6,0.2,0.2],[0.3,0.4,0.3],[0,0.3,0.7]],dtype='float32')
start_matrix = np.array([[0.5,0.3,0.2]],dtype='float32')

value1 = []
value2 = []
value3 = []
for i in range(30):
    start_matrix = np.dot(start_matrix,transfer_matrix)
    value1.append(start_matrix[0][0])
    value2.append(start_matrix[0][1])
    value3.append(start_matrix[0][2])
print(start_matrix)

[[0.23076934 0.30769244 0.4615386 ]]

#进行可视化
x = np.arange(30)
plt.plot(x,value1,label='cheerful')
plt.plot(x,value2,label='so-so')
plt.plot(x,value3,label='sad')
plt.legend()
plt.show()

可以发现，从10轮左右开始，我们的状态概率分布就不变了，一直保持在[0.23076934,0.30769244,0.4615386]。

我们现在换一个初始概率分布试一试$[0.2,0.3,0.5]$

start_matrix = np.array([[0.2,0.3,0.5]],dtype='float32')

value1 = []
value2 = []
value3 = []
for i in range(30):
    start_matrix = np.dot(start_matrix,transfer_matrix)
    value1.append(start_matrix[0][0])
    value2.append(start_matrix[0][1])
    value3.append(start_matrix[0][2])

print(start_matrix)

[[0.2307693 0.3076924 0.4615386]]

plt.plot(x,value1,label='cheerful')
plt.plot(x,value2,label='so-so')
plt.plot(x,value3,label='sad')
plt.legend()
plt.show()

可以看出，尽管这次我们采用了不同初始概率分布，最终状态的概率分布趋于同一个稳定的概率分布[0.23076934,0.30769244,0.4615386]，也就是说我们的马尔科夫链模型的状态转移矩阵收敛到的稳定概率分布与我们的初始状态概率分布无关。也就是说，如果我们得到了这个稳定概率分布对应的马尔科夫链模型的状态转移矩阵，则我们可以用任意的概率分布样本开始，带入马尔科夫链模型的状态转移矩阵，这样经过一些序列的转换，最终就可以得到符合对应稳定概率分布的样本。

同时，对于一个确定的状态转移矩阵 $P$ ，它的 $n$ 次幂 $P^{n}$ 在当 $n$ 大于一定的值的时候也可以发现是确定的

value1 = []
value2 = []
value3 = []
value4 = []
value5 = []
value6 = []
value7 = []
value8 = []
value9 = []
transfer_matrix = np.array([[0.6,0.2,0.2],[0.3,0.4,0.3],[0,0.3,0.7]],dtype='float32')
matrix = np.array([[0.6,0.2,0.2],[0.3,0.4,0.3],[0,0.3,0.7]],dtype='float32')
for i in range(30):
    matrix = np.dot(matrix,transfer_matrix)
    value1.append(matrix[0][0])
    value2.append(matrix[0][1])
    value3.append(matrix[0][2])
    value4.append(matrix[1][0])
    value5.append(matrix[1][1])
    value6.append(matrix[1][2])
    value7.append(matrix[2][0])
    value8.append(matrix[2][1])
    value9.append(matrix[2][2]) 

print(matrix)

[[0.23076935 0.3076924  0.46153858]
 [0.23076938 0.30769247 0.46153867]
 [0.23076937 0.30769247 0.4615387 ]]

plt.plot(x,value1,label='value1')
plt.plot(x,value2,label='value2')
plt.plot(x,value3,label='value3')
plt.plot(x,value4,label='value4')
plt.plot(x,value5,label='value5')
plt.plot(x,value6,label='value6')
plt.plot(x,value7,label='value7')
plt.plot(x,value8,label='value8')
plt.plot(x,value9,label='value9')
plt.legend()
plt.show()

从上可以看出，马尔可夫链在几个时期内对随机变量建模是不合理的方法，但可以用来计算该变量的长期趋势，且与初始状态无关。

用数学语言总结下马尔科夫链的收敛性质：

如果一个非周期的马尔科夫有状态转移矩阵 $P$ ，并且他的任何两个状态是连通的，那么 $\underset{n\rightarrow \infty}{lim}P_{ij}^{n}$ 与 $i$ 无关，我们有：

$\underset{n\rightarrow \infty}{lim}P_{ij}^{n}=\pi(j)$
$\underset{n\rightarrow \infty}{lim}P^{n}=\begin{bmatrix}\pi(1) &\pi(2) &\cdots &\pi(j) & \cdots \\ \pi(1) &\pi(2) &\cdots &\pi(j) & \cdots \\ \vdots & \vdots & \vdots &\ddots &\vdots \\ \pi(1) &\pi(2) &\cdots &\pi(j) & \cdots \\ \vdots & \vdots & \vdots & \ddots & \vdots \end{bmatrix}$
$\pi(j)=\sum_{i=0}^{\infty}\pi(i)P_{ij}$
$\pi$ 是方程 $\pi P =\pi$ 唯一非负解，其中 $\pi=\left[\pi(1) ,\pi(2) ,\cdots ,\pi(j) , \cdots \right]\sum_{i=1}^{\infty}\pi(i)=1$ ， $\pi$ 称为马氏链的平稳分布。

注意：

非周期的马尔科夫链：这个主要是指马尔科夫链的状态转化不是循环的，如果是循环的则永远不会收敛。幸运的是我们遇到的马尔科夫链一般都是非周期性的。用数学方式表述则是：对于任意某一状态 $i$ , $d$ 为集合 $\{n|n\geqslant1,P_{ii}^{n}>0\}$ 的最大公约数，如果 $d=1$ ，则该状态为非周期的。
任何两个状态是连通的：这个指的是从任意一个状态可以通过有限步到达其他的任意一个状态，不会出现条件概率一直为0导致不可达的情况，即 $P^{n}$ 中任意一个元素都大于零。
马尔科夫链的状态数可以是有限的，也可以是无限的。因此可以用于连续概率分布和离散概率分布。
我们用 $X_{i}$ 表示在马氏链上跳转第 $i$ 步后所处的状态，如果 $\underset{n\rightarrow \infty}{lim}P_{ij}^{n}=\pi(j)$ 存在，很容易证明以上定理的第三个结论。由于

$P(X_{n+1}=j)=\sum_{i=0}^{\infty}P(X_{n}=i)P(X_{n+1}=j|X_{n}=i)=\sum_{i=0}^{\infty}P(X_{n}=i)P_{ij}\\$

两边去极限就可以得到：

$\pi(j)=\sum_{i=0}^{\infty}\pi(i)P_{ij}\\$ 5. 由马氏链收敛的定理, 概率分布 $\pi_{i}(x)$ 将收敛到平稳分布 $\pi(x)$ 。假设到第 $n$ 步的时候马氏链收敛，则有 $X_{n}\sim \pi(x),X_{n+1}\sim \pi(x),X_{n+2}\sim \pi(x),\cdots$ ，所以 $X_{n},X_{n+1},X_{n+2},\cdots \pi(x)$ 都是同分布的随机变量，当然他们并不独立。如果我们从一个具体的初始状态 $x_{0}$ $x_{0}$开始, 沿着马氏链按照概率转移矩阵做跳转，那么我们得到一个转移序列 $x_{0},x_{1},x_{2},\cdots,x_{n-1},x_{n},x_{n+1},\cdots$ ，由于马氏链的收敛行为， $x_{n},x_{n+1},\cdots$ 都将是平稳分布 $\pi(x)$ 的样本。

3.3 基于马尔科夫链采样

如果我们得到了某个平稳分布所对应的马尔科夫链状态转移矩阵，我们就很容易采用出这个平稳分布的样本集。

首先，基于初始任意简单概率分布比如高斯分布 $\pi_{0}(x)$ 采样得到状态值 $x_{0}$ ，基于条件概率分布 $P(x|x_{0})$ 采样状态值 $x_{1}$ ，一直进行下去，当状态转移进行到一定的次数时，比如到 $n$ 次时，我们认为此时的采样集 $(x_{n},x_{n+1},...)$ 即是符合我们的平稳分布的对应样本集，可以用来做蒙特卡罗模拟求和了。

算法如下：

输入马尔科夫链状态转移矩阵 $P$ ，设定状态转移次数阈值 $n_{1}$ ，需要的样本个数 $n_{2}$ ；
从任意简单概率分布采样得到初始状态值 $x_{0}$ ；
for $t=0 ~to~ n_{1}+n_{2}-1$ : 从条件概率分布 $P(x|x_{t})$ 中采样得到样本 $x_{t+1}$ ；
样本集 $(x_{n},x_{n+1},...)$ 即是符合我们的平稳分布的对应样本集。

3.4 马尔科夫链采样小结

如果假定我们可以得到我们需要采样样本的平稳分布所对应的马尔科夫链状态转移矩阵，那么我们就可以用马尔科夫链采样得到我们需要的样本集，进而进行蒙特卡罗模拟。

但是一个重要的问题是，随意给定一个平稳分布 $\pi$ ,如何得到它所对应的马尔科夫链状态转移矩阵P呢？MCMC是时候出现了。

3.5 补充：PageRank：Google的民主表决式网页排名技术

"PageRank"的网页排名算法是Google的革命性发明。这项技术在1998年前后使得搜索的相关性有了质的飞跃，甚至有人认为Google的成功是基于这个算法。当然有点夸大。

最先试图给互联网上的众多网站排序的是雅虎公司，杨致远和费罗最早使用的是目录分类方式让用户通过互联网检索信息。但是由于计算机存储容量限制，收入的网页很少，而且只能对网页中常见内容相关的实际用词进行索引。导致查找一个文献需要换好几个搜索引擎。后来的AltaVista用了Alpha服务器，解决了覆盖问题，但是不能很好的对结果进行排序。直到Google创始人拉里$\cdot$佩奇和谢盖尔$\cdot$布林找到完善的模型。“PageRank”的核心思想就是如果一个网页被很多其他网页所链接，说明它受到普遍的承认和信赖，那么它的排名就高。当然实际并不是这么简单，还需考虑各个网页的权重。但是权重该如何度量呢？佩奇认为用网页排名，那这岂不是成了”先有鸡还是先有蛋“的问题了吗？布林破解了怪圈，他将这个问题变成二维矩阵相乘问题，先假定初始排名相同，然后进行迭代直到收敛。他俩从理论证明了无论初始值如何选，这种算法都能保证网页排名的估计值收敛到真实值。这其实就是马尔科夫的收敛性。

当然如今决定搜索质量最有用的已不是网页与网页之间的关系，而是用户的点击信息。

4：马尔可夫链蒙特卡罗算法

4.1 马尔科夫链的细致平稳条件(Detailed Balance Condition)

在解决从平稳分布 $\pi$ , 找到对应的马尔科夫链状态转移矩阵 $P$ 之前，我们还需要先看看马尔科夫链的细致平稳条件。定义如下：

如果非周期马尔科夫链状态转移矩阵 $P$ 和概率分布 $\pi(x)$ 对所与的 $i,j$ 满足：

$\pi(i)P(i,j)=\pi(j)P(j,i),~~for ~all~ i,j\\$

则称概率分布 $\pi(x)$ 是状态转移矩阵 $P$ 的平稳分布(Stationary Distribution)。

上述只是个充分条件，证明如下：

因为 $\sum_{i}\pi(i)P(i,j)=\sum_{i}\pi(j)P(j,i)=\pi(j)\sum_{i}P(j,i)=\pi(j)$ ，所以 $\pi P =\pi$ 。

当分布是二维时，此条件是充要的，但3维以上时，就不是了。

这里证明二维时条件的必要性，将上面例子形式化表示：

$\textbf{v}=[\upsilon _{1},\upsilon _{2}]\\$

$\textbf{P}=\begin{bmatrix}p_{11} &p_{12} \\ p_{21} &p_{22} \end{bmatrix}\\$

当达到稳定值时，当前 $\textbf{v}^{t}$ 等于下一步的 $\textbf{v}^{t+1}$ ，即：

$\textbf{v}^{t}\textbf{P}=[\upsilon _{1}^{t},\upsilon _{2}^{t}]\begin{bmatrix}p_{11} &p_{12} \\ p_{21} &p_{22} \end{bmatrix}=[\upsilon _{1}^{t}p_{11}+\upsilon _{2}^{t}p_{21},\upsilon _{1}^{t}p_{12}+\upsilon _{2}^{t}p_{22}]=[\upsilon _{1}^{t+1},\upsilon _{2}^{t+1}]$

即：

$\upsilon _{1}^{t}p_{11}+\upsilon _{2}^{t}p_{21}=\upsilon _{1}^{t+1}\\$ $\upsilon _{1}^{t}p_{12}+\upsilon _{2}^{t}p_{22}=\upsilon _{2}^{t+1}\\$

稳定时： $\upsilon _{1}^{t}=\upsilon _{1}^{t+1},\upsilon _{2}^{t}=\upsilon _{2}^{t+1}$ ，我们统一写作 $\upsilon _{1},\upsilon _{2}$ ，所以：

$\upsilon _{1}p_{11}+\upsilon _{2}p_{21}=\upsilon _{1}\\$

$\upsilon _{1}p_{12}+\upsilon _{2}p_{22}=\upsilon _{2}\\$

两个等式简化后都是一样的：

$\upsilon _{1}p_{12}=\upsilon _{2}p_{21}\\$

证毕。

从细致平稳条件可以得到，只要我们找到了可以使概率分布 $\pi(x)$ 满足细致平稳分布的矩阵 $P$ 即可。这给了我们寻找从平稳分布 $\pi$ , 找到对应的马尔科夫链状态转移矩阵 $P$ 的新思路。

不过不幸的是，我们很难找到合适的矩阵 $P$ 满足细致平稳条件。

4.2 MCMC采样

由于一般情况下，目标平稳分布 $\pi(x)$ 和某一个马尔科夫链状态转移矩阵 $Q$ 不满足细致平稳条件，即：

$\pi(i)Q(i,j)\neq\pi(j)Q(j,i)\\$

以下记号表达同一个意思： $Q(i,j)\Leftrightarrow Q(j|i))\Leftrightarrow Q(i\rightarrow j)$

我们引入一个 $\alpha(i,j)$ ,使上式可以取等号。

$\pi(i)Q(i,j)\alpha(i,j)=\pi(j)Q(j,i)\alpha(j,i)\\$

怎样才能成立呢，其实很简单，按照对称性：

$\alpha(i,j)=\pi(j)Q(j,i); \pi(i)Q(i,j)=\alpha(j,i)\\$

然后我们就可以得到了分布 $\pi(x)$ 对让马尔科夫链状态转移矩阵 $P(i,j)=Q(i,j)\alpha(i,j)$

其中 $\alpha(i,j)$ 一般称之为接受率，取值在 $[0,1]$ 之间，可以理解为一个概率值。这很像接受-拒绝采样，那里是以一个常用分布通过一定的接受-拒绝概率得到一个非常见分布，这里是以一个常见的马尔科夫链状态转移矩阵 $Q$ 通过一定的接受-拒绝概率得到目标转移矩阵 $P$ ,两者的解决问题思路是类似的。

MCMC采样算法如下：

输入任意给定的马尔科夫链状态转移矩阵 $Q$ ，目标平稳分布 $\pi(x)$ ，设定状态转移次数阈值 $n_{1}$ ，需要的样本数 $n_{2}$ ;
从任意简单概率分布得到初始状态值 $x_{0}$ ；
for $t=0 ~in ~n_{1}+n_{2}-1$

a. 从条件概率分布 $Q(x|x_{t})$ 得到样本值 $x_{*}$
b. 从均匀分布中采样 $U\sim[0,1]$
c. 如果 $u<\alpha(x_{t},x_{*})=\pi(x_{*})Q(x_{*},x_{t})$ ，则接受 $x_{t}\rightarrow x_{*}$ ，即 $x_{t+1}= x_{*}$
d. 否则不接受转移， $t=max\{t-1,0\}$

上述过程中 $p(x),q(x|y)$ 说的都是离散的情形，事实上即便这两个分布是连续的，以上算法仍然是有效，于是就得到更一般的连续概率分布 $p(x)$ 的采样算法，而 $q(x|y)$ 就是任意一个连续二元概率分布对应的条件分布。

但是这个采样算法还是比较难在实际中应用，因为在第三步中，由于 $\alpha(x_{t},x_{*})$ 可能非常的小，比如0.1，导致我们大部分的采样值都被拒绝转移，采样效率很低。有可能我们采样了上百万次马尔可夫链还没有收敛，也就是上面这个 $n_{1}$ 要非常非常的大，这让人难以接受，怎么办呢？这时就轮到我们的M-H采样出场了。

5： M-H采样

5.1 M-H采样算法

M-H采样是Metropolis-Hastings采样的简称，这个算法首先由Metropolis提出，被Hastings改进，因此被称之为Metropolis-Hastings采样或M-H采样。

M-H采样解决了我们上一节MCMC采样接受率过低的问题。

我们可以对 $\pi(i)Q(i,j)\alpha(i,j)=\pi(j)Q(j,i)\alpha(j,i)$ 两边进行扩大，此时细致平稳条件也是满足的，我们将等式扩大 $C$ 倍，使 $C\alpha(j,i)=1$ （精确来说是使得两边最大的扩大为1），这样我们就提高了采样中的跳转接受率，所以我们可以取 $\alpha(i,j)=min\{\frac{\pi(j)Q(j,i)}{\pi(i)Q(i,j)},1\}$

M-H采样算法如下：

输入任意给定的马尔科夫链状态转移矩阵 $Q$ ，目标平稳分布 $\pi(x)$ ，设定状态转移次数阈值 $n_{1}$ ，需要的样本数 $n_{2}$ ;
从任意简单概率分布得到初始状态值 $x_{0}$ ；
for $t=0 ~in ~n_{1}+n_{2}-1$

a. 从条件概率分布 $Q(x|x_{t})$ 得到样本值 $x_{*}$
b. 从均匀分布中采样 $U\sim[0,1]$
c. 如果 $u<\alpha(x_{t},x_{*})=min\{\frac{\pi(*)Q(x_{*},x_{t})}{\pi(t)Q(x_{t},x_{*})},1\}$ ，则接受 $x_{t}\rightarrow x_{*}$ ，即 $x_{t+1}= x_{*}$
d. 否则不接受转移， $t=max\{t-1,0\}$

很多时候我们马尔科夫转移状态矩阵是对称的，因此接受率可以写成： $\alpha(i,j)=min\{\frac{\pi(j)}{\pi(i)},1\}$

对于分布 $p(x)$ , 我们构造转移矩阵 $P$ 使其满足细致平稳条件:

$\pi(x)P(x\rightarrow y)=\pi(y)P(y\rightarrow x)$

此处 $x$ 并不要求是一维的，对于高维空间的 $p(\mathbf{x})$ ，如果满足细致平稳条件

$\pi(\mathbf{x})P(\mathbf{x}\rightarrow \mathbf{y})=\pi(\mathbf{y})P(\mathbf{y}\rightarrow \mathbf{x})$

那么以上的 Metropolis-Hastings 算法一样有效。

5.2 M-H采样python实现

假设目标平稳分布是一个均值3，标准差2的正态分布，而选择的马尔可夫链状态转移矩阵 $Q(i,j)$ 的条件转移概率是以 $i$ 为均值,方差1的正态分布在位置 $j$ 的值。

from scipy.stats import norm

def norm_dist_prob(theta):
    y = norm.pdf(theta, loc=3, scale=2)
    return y

T = 5000
pi = [0 for i in range(T)]
sigma = 1
t = 0
while t < T-1:
    t = t + 1
    pi_star = norm.rvs(loc=pi[t - 1], scale=sigma, size=1, random_state=None)   #状态转移进行随机抽样
    alpha = min(1, (norm_dist_prob(pi_star[0]) / norm_dist_prob(pi[t - 1])))   #alpha值

    u = random.uniform(0, 1)
    if u < alpha:
        pi[t] = pi_star[0]
    else:
        pi[t] = pi[t - 1]


plt.scatter(pi, norm.pdf(pi, loc=3, scale=2),label='Target Distribution')
num_bins = 50
plt.hist(pi, num_bins, normed=1, facecolor='red', alpha=0.7,label='Samples Distribution')
plt.legend()
plt.show()

5.3 M-H采样小结

在大数据时代，M-H采样面临着两大难题：

1）我们的数据特征非常的多，M-H采样由于接受率计算式 $min\{\frac{\pi(j)Q(j,i)}{\pi(i)Q(i,j)},1\}$ 的存在，在高维时需要的计算时间非常的可观，算法效率很低。同时 $\alpha(i,j)$ 一般小于1，有时候辛苦计算出来却被拒绝了。能不能做到不拒绝转移呢？

2）由于特征维度大，很多时候我们甚至很难求出目标的各特征维度联合分布，但是可以方便求出各个特征之间的条件概率分布。这时候我们能不能只有各维度之间条件概率分布的情况下方便的采样呢？

6： Gibbs采样

6.1 重新寻找合适的细致平稳条件

细致平稳条件：如果非周期马尔科夫链状态转移矩阵 $P$ 和概率分布 $\pi(x)$ 对所与的 $i,j$ 满足：

$\pi(i)P(i,j)=\pi(j)P(j,i)\\$

则称概率分布 $\pi(x)$ 是状态转移矩阵 $P$ 的平稳分布。

在M-H采样中我们通过引入接受率使细致平稳条件满足。现在我们换一个思路。

从二维的数据分布开始，假设 $\pi(x_{1},x_{2})$ 是一个二维联合数据分布，观察第一个特征维度相同的两个点 $A(x_{1}^{(1)},x_{2}^{(1)})$ 和 $B(x_{1}^{(1)},x_{2}^{(2)})$ ，容易发现下面两式成立：

$\pi(x_{1}^{(1)},x_{2}^{(1)})\pi(x_{2}^{(2)}|x_{1}^{(1)})=\pi(x_{1}^{(1)})\pi(x_{2}^{(1)}|x_{1}^{(1)})\pi(x_{2}^{(2)}|x_{1}^{(1)})\\$

$\pi(x_{1}^{(1)},x_{2}^{(2)})\pi(x_{2}^{(1)}|x_{1}^{(1)})=\pi(x_{1}^{(1)})\pi(x_{2}^{(2)}|x_{1}^{(1)})\pi(x_{2}^{(1)}|x_{1}^{(1)})\\$

由于两式的右边相等，因此我们有：

$\pi(x_{1}^{(1)},x_{2}^{(1)})\pi(x_{2}^{(2)}|x_{1}^{(1)})=\pi(x_{1}^{(1)},x_{2}^{(2)})\pi(x_{2}^{(1)}|x_{1}^{(1)})\\$

也就是：

$\pi(A)\pi(x_{2}^{(2)}|x_{1}^{(1)})=\pi(B)\pi(x_{2}^{(1)}|x_{1}^{(1)})\\$

观察上式再观察细致平稳条件的公式，我们发现在 $x_{1}=x_{1}^{(1)}$ 这条直线上，如果用条件概率分布 $\pi(x_{2}|x_{1}^{(1)})$ 作为马尔科夫链的状态转移概率，则任意两个点之间的转移满足细致平稳条件！同样的道理，在 $x_{2}=x_{2}^{(1)}$ 这条直线上，如果用条件概率分布 $\pi(x_{1}|x_{2}^{(1)})$ 作为马尔科夫链的状态转移概率，则任意两个点之间的转移也满足细致平稳条件。那是因为假如有一点 $C(x_{1}^{(2)},x_{2}^{(1)})$ ,我们可以得到：

$\pi(A)\pi(x_{1}^{(2)}|x_{2}^{(1)})=\pi(C)\pi(x_{1}^{(1)}|x_{2}^{(1)})\\$

基于上面的发现，我们可以这样构造分布 $\pi(x_{1}),\pi(x_{2})$ 的马尔可夫链对应的状态转移矩阵 $P$ :

$P(A\rightarrow B)=\pi(x_{2}^{(B)}|x_{1}^{(1)})~~ if~~ x_{1}^{(A)}=x_{1}^{(B)}=x_{1}^{(1)}\\$

$P(A\rightarrow C)=\pi(x_{1}^{(C)}|x_{2}^{(1)}) ~~if~~ x_{2}^{(A)}=x_{2}^{(C)}=x_{2}^{(1)}\\$

$P(A\rightarrow D)=0 ~~else\\$

有了上面这个状态转移矩阵，我们很容易验证平面上的任意两点 $E,F$ ，满足细致平稳条件：

$\pi(E)P(E\rightarrow F)=\pi(F)P(F\rightarrow E)\\$

6.2 二维Gibbs采样

利用上一节找到的状态转移矩阵，我们就得到了二维Gibbs采样，这个采样需要两个维度之间的条件概率。算法如下：

输入平稳分布 $\pi(x_{1},x_{2})$ ，设定状态转移次数阈值 $n_{1}$ ，需要的样本个数 $n_{2}$ ;
随机初始化初始状态值 $x_{1}^{(1)}$ 和 $x_{2}^{(1)}$ ;
for $t=0 ~to ~n_{1}+n_{2}-1$ :

从条件概率分布 $p(x_{2}|x_{1}^{t})$ 中采样得到样本 $x_{2}^{t+1}$
从条件概率分布 $p(x_{1}|x_{2}^{t+1})$ 中采样得到样本 $x_{1}^{t+1}$

样本集： $\{(x_{1}^{(n_{1})},x_{2}^{(n_{1})}),(x_{1}^{(n_{1}+1)},x_{2}^{(n_{1}+1)}),\dots,(x_{1}^{(n_{1}+n_{2}-1)},x_{2}^{(n_{1}+n_{2}-1)})\}$ 即为我们需要的平稳分布对应的样本集。

整个采样过程中，马氏链的转移只是轮换的沿着坐标轴，采样的过程为：

$(x_{1}^{(1)},x_{2}^{(1)})\rightarrow (x_{1}^{(1)},x_{2}^{(2)})\rightarrow (x_{1}^{(2)},x_{2}^{(2)})\rightarrow \cdots \rightarrow (x_{1}^{(n_{1}+n_{2}-1)},x_{2}^{(n_{1}+n_{2}-1)})$

马氏链收敛后，最终得到的样本就是 $p(x,y)$ 的样本，而收敛之前的阶段称为 burn-in period。额外说明一下，我们看到教科书上的 Gibbs Sampling 算法大都是坐标轴轮换采样的，但是这其实是不强制要求的。最一般的情形可以是，在 $t$ 时刻，可以在 $x$ 轴和 $y$ 轴之间随机的选一个坐标轴，然后按条件概率做转移，马氏链也是一样收敛的。轮换两个坐标轴只是一种方便的形式。

6.3 多维Gibbs采样

上面的这个算法推广到多维的时候也是成立的。比如一个 $n$ 维的概率分布 $\pi(x_{1},x_{2},...,x_{n})$ ，可以通过在 $n$ 个坐标轴上轮换采样，来得到新的样本。对于轮换到的任意一个坐标轴 $x_{i}$ 上的转移，马尔科夫链的状态转移概率为 $P(x_{i}|x_{1},x_{2},..,x_{i-1},x_{i+1},...,x_{n})$ ，即固定 $n−1$ 个坐标轴，在某一个坐标轴上移动，即每次转移只允许某一个维度上变化，可以解决维数灾难问题。算法如下：

输入平稳分布 $\pi(x_{1},x_{2},...,x_{n})$ ，设定状态转移次数阈值 $n_{1}$ ，需要的样本个数 $n_{2}$
随机初始化初始状态值 $x_{1}^{(1)},x_{2}^{(1)},...,x_{n}^{(1)})$
for $t=0~ to~ n_{1}+n_{2}-1$ :

从条件概率分布 $p(x_{1}|x_{2}^{t},x_{3}^{t},...,x_{n}^{t})$ 中采样得到样本 $x_{1}^{t+1}$
从条件概率分布 $p(x_{2}|x_{1}^{t+1},x_{3}^{t},...,x_{n}^{t})$ 中采样得到样本 $x_{2}^{t+1}$
....
从条件概率分布 $p(x_{j}|x_{1}^{t+1},x_{2}^{t+1},x_{j-1}^{t+1},x_{j+1}^{t}...,x_{n}^{t})$ 中采样得到样本 $x_{j}^{t+1}$
....
从条件概率分布 $p(x_{n}|x_{1}^{t+1},x_{2}^{t+1},...,x_{n-1}^{t+1})$ 中采样得到样本 $x_{n}^{t+1}$

样本集： $\{(x_{1}^{(n_{1})},x_{2}^{(n_{1})},...,x_{n}^{(n_{1})}),\dots,(x_{1}^{(n_{1}+n_{2}-1)},x_{2}^{(n_{1}+n_{2}-1)},...,x_{n}^{(n_{1}+n_{2}-1)})\}$ 即为我们需要的平稳分布对应的样本集。当然这些样本并不独立，但是我们此处要求的是采样得到的样本符合给定的概率分布，并不要求独立。

整个采样过程和Lasso回归的坐标轴下降法算法非常类似，只不过Lasso回归是固定 $n−1$ 个特征，对某一个特征求极值。而Gibbs采样是固定 $n−1$ 个特征在某一个特征采样。

同样的，轮换坐标轴不是必须的，我们可以随机选择某一个坐标轴进行状态转移，只不过常用的Gibbs采样的实现都是基于坐标轴轮换的。

6.4 二维Gibbs采样实例python实现

假设我们要采样的是一个二维正态分布 $N(\mu,\Sigma)$ ，其中： $\mu=(\mu_{1},\mu_{2})=(5,-1)$ ， $\Sigma=\begin{pmatrix}\sigma_{1}^{2} &\rho \sigma_{1}\sigma_{2} \\ \rho \sigma_{1}\sigma_{2} & \sigma_{2}^{2}\end{pmatrix}=\begin{pmatrix}1 &1 \\ 1 & 4\end{pmatrix}$ ;

而采样过程中的需要的状态转移条件分布为：

$P(x_{1}|x_{2})=N\left(\mu_{1}+\rho \sigma_{1}/\sigma_{2}(x_{2}-\mu_{2}),(1-\rho^{2})\sigma_{1}^{2}\right)\\$

$P(x_{2}|x_{1})=N\left(\mu_{2}+\rho \sigma_{2}/\sigma_{1}(x_{1}-\mu_{1}),(1-\rho^{2})\sigma_{2}^{2}\right)\\$

from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal

samplesource = multivariate_normal(mean=[5,-1], cov=[[1,0.5],[0.5,2]])

def p_ygivenx(x, m1, m2, s1, s2):
    return (random.normalvariate(m2 + rho * s2 / s1 * (x - m1), math.sqrt(1 - rho ** 2) * s2))

def p_xgiveny(y, m1, m2, s1, s2):
    return (random.normalvariate(m1 + rho * s1 / s2 * (y - m2), math.sqrt(1 - rho ** 2) * s1))

N = 5000
K = 20
x_res = []
y_res = []
z_res = []
m1 = 5
m2 = -1
s1 = 1
s2 = 2

rho = 0.5
y = m2

for i in range(N):
    for j in range(K):
        x = p_xgiveny(y, m1, m2, s1, s2)   #y给定得到x的采样
        y = p_ygivenx(x, m1, m2, s1, s2)   #x给定得到y的采样
        z = samplesource.pdf([x,y])
        x_res.append(x)
        y_res.append(y)
        z_res.append(z)

num_bins = 50
plt.hist(x_res, num_bins, normed=1, facecolor='green', alpha=0.5,label='x')
plt.hist(y_res, num_bins, normed=1, facecolor='red', alpha=0.5,label='y')
plt.title('Histogram')
plt.legend()
plt.show()

然后我们看看样本集生成的二维正态分布，代码如下：

fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
ax.scatter(x_res, y_res, z_res,marker='o')
plt.show()

6.5 Gibbs采样小结

由于Gibbs采样在高维特征时的优势，目前我们通常意义上的MCMC采样都是用的Gibbs采样。当然Gibbs采样是从M-H采样的基础上的进化而来的，同时Gibbs采样要求数据至少有两个维度，一维概率分布的采样是没法用Gibbs采样的,这时M-H采样仍然成立。

有了Gibbs采样来获取概率分布的样本集，有了蒙特卡罗方法来用样本集模拟求和，他们一起就奠定了MCMC算法在大数据时代高维数据模拟求和时的作用。

7：参考：

MCMC(一)蒙特卡罗方法 - 刘建平Pinard - 博客园

MCMC(二)马尔科夫链 - 刘建平Pinard - 博客园

MCMC(三)MCMC采样和M-H采样 - 刘建平Pinard - 博客园

MCMC(四)Gibbs采样 - 刘建平Pinard - 博客园

Markov Chain Monte Carlo Without all the Bullshit

LDA-math-MCMC 和 Gibbs Sampling

http://www.columbia.edu/~ks20/4703-Sigman/4703-07-Notes-ARM.pdf

论智：告别数学公式，图文解读什么是马尔可夫链蒙特卡罗方法（MCMC）

马尔可夫链蒙特卡洛(MCMC)采样 - nobullshit

30分钟了解蒙特卡洛方法

机器学习小组知识点30：接受-拒绝采样（Acceptance-Rejection Sampling）

马尔科夫链细致平衡条件

吴军：《数学之美》第二版

posted on 2019-12-03 17:07 曹明阅读(1678) 评论(0) 收藏举报

马尔可夫链蒙特卡罗算法（MCMC）

马尔可夫链蒙特卡罗算法（MCMC）

1: MCMC

2： 蒙特卡罗

2.3 拒绝接受采样（Acceptance-Rejection Sampling）

3 马尔科夫链

4： 马尔可夫链蒙特卡罗算法

5： M-H采样

6： Gibbs采样

7： 参考：

2：蒙特卡罗

4：马尔可夫链蒙特卡罗算法

7：参考：