Python数据类型2

一、Python实现栈

栈是一种运算受限的线性表，栈只允许在表的一端进行插入和删除操作，这一端被称为栈顶（Top），相对地把另一端称为栈底（Bottom）。把新元素放到栈顶元素的上面，使之成为新的栈顶元素称作进栈、入栈或压栈（Push）；把栈顶元素删除，使其相邻的元素成为新的栈顶元素称作出栈或退栈（Pop）。这种受限的运算使栈拥有“先进后出”的特性（First In Last Out），简称 FILO。

可以通过下面方法实现栈：

 

#列表实现栈

class ListStack:
    def __init__(self):
        """初始化一个空栈"""
        self.items = []  # 使用列表存储栈元素

    def push(self, item):
        """入栈操作：将元素添加到栈顶。时间复杂度 O(1)。"""
        self.items.append(item)

    def pop(self):
        """出栈操作：移除并返回栈顶元素。时间复杂度 O(1)。"""
        if self.is_empty():
            raise IndexError("pop from an empty stack")  # 空栈时抛出异常[3,5](@ref)
        return self.items.pop()

    def peek(self):
        """查看栈顶元素：返回栈顶元素但不移除它。时间复杂度 O(1)。"""
        if self.is_empty():
            raise IndexError("peek from an empty stack")  # 空栈时抛出异常[3,5](@ref)
        return self.items[-1]

    def is_empty(self):
        """检查栈是否为空"""
        return len(self.items) == 0

    def size(self):
        """返回栈中元素的个数"""
        return len(self.items)

    def __str__(self):
        """返回栈的字符串表示，方便查看"""
        return str(self.items)



# 创建一个栈对象
my_stack = ListStack()

# 检查栈是否为空
print(my_stack.is_empty())  # 输出: True

# 执行入栈操作
my_stack.push(10)
my_stack.push(20)
my_stack.push(30)

print(my_stack)     # 输出: [10, 20, 30]
print(my_stack.size()) # 输出: 3

# 查看栈顶元素
print(my_stack.peek())  # 输出: 30

# 执行出栈操作
print(my_stack.pop())   # 输出: 30
print(my_stack.pop())   # 输出: 20

print(my_stack.size()) # 输出: 1
print(my_stack.is_empty()) # 输出: False

print(my_stack.pop())   # 输出: 10
print(my_stack.is_empty()) # 输出: True

# 尝试从空栈弹出元素会引发异常
# my_stack.pop() # IndexError: pop from an empty stack

 

#单链表方法实现栈
#定义节点
class Node():
    def __init__(self, elem, _next = None):
        self.elem = elem
        self.next = _next

#链表实现栈
class Lstack():
    def __init__(self):
        #初始化栈顶元素
        self._top = None
    #判断是否为空
    def is_empty(self):
        return self._top is None
    #查看栈顶元素
    def top(self):
        if self.is_empty():
            print("空栈")
            return
        return self._top.elem
    #入栈
    def push(self,elem):
        self._top = Node(elem, self._top)
    #出栈
    def pop(self):
        if self.is_empty():
            print("空栈")
            return
        re = self._top.elem
        self._top = self._top.next
        return re
s = Lstack()
s.push(2)
s.push(5)
s.push(7)
print(s.pop())
"""
结果为7
"""

 

二、python实现队列

队列是一种列表，但是队列只能在队尾加入元素，队首删除元素，队列和是 先进先出（FIFO）。

 

#列表实现队列

class Queue:
    def __init__(self):
        """初始化一个空队列"""
        self.items = []
    
    def is_empty(self):
        """检查队列是否为空"""
        return len(self.items) == 0
    
    def enqueue(self, item):
        """向队列尾部添加元素"""
        self.items.append(item)
    
    def dequeue(self):
        """从队列头部移除并返回元素"""
        if self.is_empty():
            raise IndexError("队列为空，无法执行出队操作")
        return self.items.pop(0)
    
    def front(self):
        """返回队列头部的元素（不移除）"""
        if self.is_empty():
            raise IndexError("队列为空")
        return self.items[0]
    
    def rear(self):
        """返回队列尾部的元素（不移除）"""
        if self.is_empty():
            raise IndexError("队列为空")
        return self.items[-1]
    
    def size(self):
        """返回队列中元素的数量"""
        return len(self.items)
    
    def __str__(self):
        """返回队列的字符串表示"""
        return "队列: " + " <- ".join(map(str, self.items))

# 测试队列功能
if __name__ == "__main__":
    q = Queue()
    
    print(f"队列是否为空: {q.is_empty()}")  # True
    
    # 添加元素
    q.enqueue(10)
    q.enqueue(20)
    q.enqueue(30)
    
    print(q)  # 队列: 10 <- 20 <- 30
    print(f"队列大小: {q.size()}")  # 3
    print(f"队首元素: {q.front()}")  # 10
    print(f"队尾元素: {q.rear()}")   # 30
    
    # 移除元素
    print(f"出队元素: {q.dequeue()}")  # 10
    print(q)  # 队列: 20 <- 30
    
    q.enqueue(40)
    print(q)  # 队列: 20 <- 30 <- 40
    
    print(f"出队元素: {q.dequeue()}")  # 20
    print(f"出队元素: {q.dequeue()}")  # 30
    print(f"出队元素: {q.dequeue()}")  # 40
    
    print(f"队列是否为空: {q.is_empty()}")  # True
    
    try:
        q.dequeue()  # 尝试从空队列出队
    except IndexError as e:
        print(f"错误: {e}")  # 队列为空，无法执行出队操作

 

from queue import Queue
from collections import deque

q = Queue()
#满足先进先出
q.put(1)
q.put(2)
q.put(3)
print(q.queue)
print(q.get())
print(q.get())
print(q.get())

#双端队列
dq = deque(["a","b","c"])
print(dq)
dq.append("d")
dq.appendleft("e")
print(dq)

三、Python实现链表

链表又可以分为单链表、双向链表、环形链表。链表作为数据结构的一种，与数组相比：

• 链表不占用连续的内存，采用离散的内存存储数据；数组采用一段连续的内存。
• 在添加和删除数据时，对原有数据的移动较小；而数组则需要大量移动原有的数据（在数组的中间插入一个元素，那么数组的后半部分都要往后移动一个单位）
• 链表在查询和遍历数据的时候比较慢，不像数组可以直接使用索引访问某个数据。
• 链表无法进行随机访问，只能进行顺序访问。

Python在其标准库中没有链接列表；我们可以使用的节点的概念来实现链表。链表通常由一连串节点组成，每个节点包含任意的实例数据(data fields)和一或两个用来指向上一个/或下一个节点的位置的链接（"links"）。

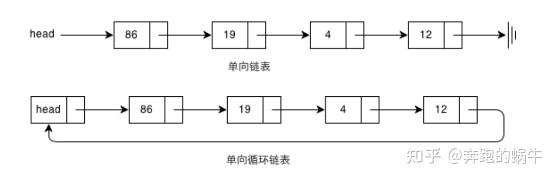
1、单向链表

单向链表也叫单链表，是链表中最简单的形式，它的每个节点包含两个域，一个信息域（元素域）和一个链接域。这个链接指向链表中的下一个节点，而最后一个节点的链接域则指向一个空值。

class LNode(object):
    #结点初始化函数, p 即模拟所存放的下一个结点的地址为了方便传参, 设置 p 的默认值为 0 
    def __init__(self, data, p=0):
        self.data = data
        self.next = p

class LinkList(object):
    def __init__(self):
        self.head = None

    #链表初始化函数, 方法类似于尾插
    def initList(self, data):
        #创建头结点
        self.head = LNode(data[0])
        p = self.head
        #逐个为 data 内的数据创建结点, 建立链表
        for i in data[1:]:
            node = LNode(i)
            p.next = node
            p = p.next

    #链表判空
    def isEmpty(self):
        if self.head.next == 0:
            print "Empty List!"
            return 1
        else:
            return 0

    #取链表长度
    def getLength(self):
        if self.isEmpty():
            exit(0)

        p = self.head
        len = 0
        while p:
            len += 1
            p = p.next
        return len

    #遍历链表
    def traveList(self):
        if self.isEmpty():
            exit(0)
        print '\rlink list traving result: ',
        p = self.head
        while p:
            print p.data,
            p = p.next

    #链表插入数据函数
    def insertElem(self, key, index):
        if self.isEmpty():
            exit(0)
        if index<0 or index>self.getLength()-1:
            print "\rKey Error! Program Exit."
            exit(0)

        p = self.head
        i = 0
        while i<=index:
            pre = p
            p = p.next
            i += 1

        #遍历找到索引值为 index 的结点后, 在其后面插入结点
        node = LNode(key)
        pre.next = node
        node.next = p

    #链表删除数据函数
    def deleteElem(self, index):
        if self.isEmpty():
            exit(0)
        if index<0 or index>self.getLength()-1:
            print "\rValue Error! Program Exit."
            exit(0)

        i = 0
        p = self.head
        #遍历找到索引值为 index 的结点
        while p.next:
            pre = p
            p = p.next
            i += 1
            if i==index:
                pre.next = p.next
                p = None
                return 1

        #p的下一个结点为空说明到了最后一个结点, 删除之即可
        pre.next = None

#初始化链表与数据
data = [1,2,3,4,5]
l = LinkList()
l.initList(data)            
l.traveList()

#插入结点到索引值为3之后, 值为666
l.insertElem(666, 3)
l.traveList()

#删除索引值为4的结点
l.deleteElem(4)
l.traveList()


#链表逆序
# 初始化，newhead=None，
# p=head：p=0—>1—>2—>3，head=head.next：head=1—>2—>3
# p.next=newhead：p=0—>None
# newhead=p：newhead=0—>None
# 循环直到head为空；
class Solution(object):
    def reverseList(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        new_head = None
        while head:
            p = head
            head = head.next
            p.next = new_head
            new_head = p
        return new_head

2、双向链表

双向链表比单向链表更加复杂，它每个节点有两个链接：一个指向前一个节点，当此节点为第一个节点时，指向空值；而另一个链接指向下一个节点，当此节点为最后一个节点时，指向空值。

head 保存首地址，item 存储数据，next 指向下一结点地址，prev 指向上一结点地址。

#定义双向链表结点
class Node(object):
    """双向链表的结点"""

    def __init__(self, item):
        # item存放数据元素
        self.item = item
        # next 指向下一个节点的标识
        self.next = None
        # prev 指向上一结点
        self.prev = None

# 定义双向链表
class BilateralLinkList(object):
    """双向链表"""

    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def length(self):
        """链表长度"""
        # 初始指针指向head
        cur = self._head
        count = 0
        # 指针指向None 表示到达尾部
        while cur is not None:
            count += 1
            # 指针下移
            cur = cur.next
        return count

    def items(self):
        """遍历链表"""
        # 获取head指针
        cur = self._head
        # 循环遍历
        while cur is not None:
            # 返回生成器
            yield cur.item
            # 指针下移
            cur = cur.next

    def add(self, item):
        """向链表头部添加元素"""
        node = Node(item)
        if self.is_empty():
            # 头部结点指针修改为新结点
            self._head = node
        else:
            # 新结点指针指向原头部结点
            node.next = self._head
            # 原头部 prev 指向 新结点
            self._head.prev = node
            # head 指向新结点
            self._head = node

    def append(self, item):
        """尾部添加元素"""
        node = Node(item)
        if self.is_empty():  # 链表无元素
            # 头部结点指针修改为新结点
            self._head = node
        else:  # 链表有元素
            # 移动到尾部
            cur = self._head
            while cur.next is not None:
                cur = cur.next
            # 新结点上一级指针指向旧尾部
            node.prev = cur
            # 旧尾部指向新结点
            cur.next = node

    def insert(self, index, item):
        """ 指定位置插入元素"""
        if index <= 0:
            self.add(item)
        elif index > self.length() - 1:
            self.append(item)
        else:
            node = Node(item)
            cur = self._head
            for i in range(index):
                cur = cur.next
            # 新结点的向下指针指向当前结点
            node.next = cur
            # 新结点的向上指针指向当前结点的上一结点
            node.prev = cur.prev
            # 当前上一结点的向下指针指向node
            cur.prev.next = node
            # 当前结点的向上指针指向新结点
            cur.prev = node

    def remove(self, item):
        """ 删除结点 """
        if self.is_empty():
            return
        cur = self._head
        # 删除元素在第一个结点
        if cur.item == item:
            # 只有一个元素
            if cur.next is None:
                self._head = None
                return True
            else:
                # head 指向下一结点
                self._head = cur.next
                # 下一结点的向上指针指向None
                cur.next.prev = None
                return True
        # 移动指针查找元素
        while cur.next is not None:
            if cur.item == item:
                # 上一结点向下指针指向下一结点
                cur.prev.next = cur.next
                # 下一结点向上指针指向上一结点
                cur.next.prev = cur.prev
                return True
            cur = cur.next
        # 删除元素在最后一个
        if cur.item == item:
            # 上一结点向下指针指向None
            cur.prev.next = None
            return True

    def find(self, item):
        """查找元素是否存在"""
        return item in self.items()

 

四、Python实现堆

堆是一种特殊的完全二叉树，当且仅当满足所有节点的值总是不大于或不小于其父节点的值的完全二叉树被称之为堆。在一个堆中，根节点是最大（或最小）节点。如果根节点最小，称之为小顶堆（或小根堆），如果根节点最大，称之为大顶堆（或大根堆）。堆的左右孩子没有大小的顺序。堆的存储一般都用数组来存储堆，i节点的父节点下标就为( i – 1 ) / 2 (i – 1) / 2(i–1)/2。它的左右子节点下标分别为 2 ∗ i + 1 2 * i + 12∗i+1 和 2 ∗ i + 2 2 * i + 22∗i+2。如第0个节点左右子节点下标分别为1和2。

 

可以使用如下方法实现堆：

 

 heapq 是一个内置堆结构，一种特殊形式的完全二叉树，其中父节点的值总是大于子节点，根据其性质，python可以用一个满足 heap[k] <= heap[2 * k + 1] <= heap[2 * k + 2] 的列表来实现。heapq是最小堆，如果要实现最大堆，可以使用一些小诀窍，例如在heappush的时候，填进去的是 数据 * -1，然后heappop的时候，将弹出的元素乘以-1即可

import heapq

heap = []
heapq.heappush(heap, 3)
heapq.heappush(heap, 2)
heapq.heappush(heap, 1)
print(heap)  # 输出为 [1, 3, 2]

# 要想有序输出 堆的元素
heapq.heappop(heap) # 输出1
heapq.heappop(heap) # 输出2
heapq.heappop(heap) # 输出3

# 要想输出前n个最大值，前n个最小值，可以使用
heapq.nlargest(n, heap)
heapq.nsmallest(n, heap)