机器学习笔记之一元线性回归

机器学习笔记_{一元线性回归}

20190201

---

感_(吐)想_(槽)

​ 机器学习，这个门入得可以说是相当艰难，感觉上花了很多时间精力去理解学习，学完后却感觉十分简单，分明用不着学那么久，而且，预测效果并不好。

​ 值得一提的是，我所在城市的新华文轩既没有花书也没有西瓜书，而我又急于入门，便选择了同样讲得很好的袁梅宇老师的机器学习基础，唯一的一点就是这本书使用MATLAB脚本实现所有程序，对之熟悉C++正想好好学学Python3的我非常不友好。

​ 此项目涉及的所有文件均已上传至GitHub:Jerry-Terrasse/LR_Olym。

---

约定

​ 这是一些符号意义的约定，这些符号都将在下文被提到。

\[x_i:训练集.年份\\ y_i:训练集.成绩\\ w:假设函数.斜率(权重)\\ b:假设函数.截距(偏置)\\ h(x):假设函数\\ J(w,b):代价函数\\ \]

---

目标

​ 机器学习试图让机器像人类那样去理解数据，从大量的数据中发现规律和提取知识，不断地完善自我。

——《机器学习基础》

​ 何谓线性，说白了就是直线，假设所有数据近似地落在一条直线上，得到这条直线也就找出了所有数据的共性。何谓回归，就是说我们找到这条直线后，反过来用它来对未知的数据点进行预测。何谓一元线性回归，就是对于一个只有一个未知数的问题，我们用一个线性函数拟合已知数据，再拿它去进行预测。

​ 这个线性函数便是我们的假设函数：

\[h(x)=wx+b \]

​ 用书中的例子具体地讲，我们的任务是预测未来两届奥运会男子100米自由泳冠军成绩。那么，我们的已知数据就是每届奥运会举办年份以及对应的冠军成绩（如下图）

​ 我们可以直观地看出，数据分布几乎是单调的，并且下降趋势比较符合直线，像这样的数据可以使用线性回归模型。我们的目标就是找出直线的斜率和截距。

代价函数

​ 上述问题可以转化为，如果事先给出斜率w和截距b，我们要能判断它们是否准确，有多么准确，并能为程序指出如何让它们更加准确。

​ 为此，我们定义代价函数：

\[J(w,b)=\frac{1}{2N}\sum_{i=1}^{N}(h(x_i)-y_i)^2 \]

​ 可以看出，这个函数的定义与方差思想相近，每一个数据点的预测值与真实值之差，平方去掉大小关系的影响，求和，再除以数据点个数以消去数据集大小影响。之所以还要除以二，是为了方便求导，这个以后再提。

​ 显而易见，当训练数据集x[] y[]确定后，J只随w b变化，即J(w,b)是w b的二元函数，我们需要找到合适的w b取值，使J最小。这样的w b取值可以简记为：

\[argmin\ J(w,b) \]

梯度下降算法

​ 于是，问题转化为熟悉的求二元函数最值问题了。。天哪听起来充满生物美感的机器学习化简到最后为什么会是这样？！诚然，我们可以愉快地对w b求偏导，令偏导数等于零，直接解出参数值，任务就完成了。（这在数学上被称为最小二乘法）可是，那还要计算机做什么呀！

​ 没错，计算机有属于计算机的、更普适的（亦可用于非线性函数）暴力方法。

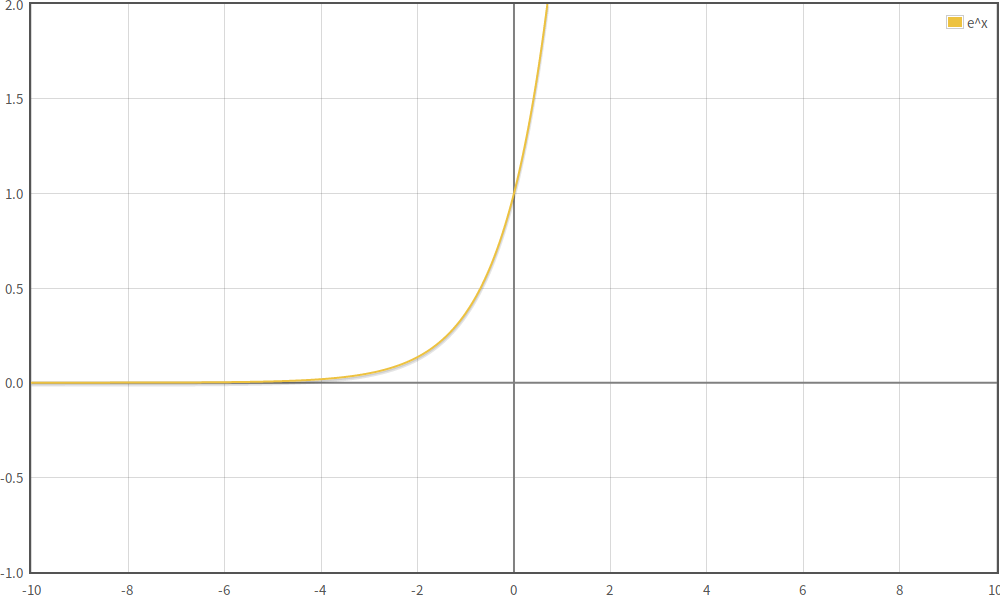
​ 请看这个一元函数f(x)=e^x的图像，它是单调递增的，当我们在它的任何一点上时，我们如何知道向左或是向右能到达更低的地方？显然，沿着函数向左走便是了。可我们的J却比这复杂得多，没那么直观，我们必须找一个更加程式化的语言来描述”向下走“的行为。

​ 我们发现，导数是个好选择。

\[f'(x_0)>0\\ \Rightarrow f(x)在x_0的某个去心邻域单调递增\\ \Rightarrow 我们得向左走\\ \Rightarrow 让x减小\\ f'(x_0)<0同理\\ \]

​ 这说明，我们只需要

---

Unfinished

---

​ 另外，我们再感性地做个理解：如果在某处导数绝对值比较大，说明此处下降/上升较快，导数减小/增大一般不会突变，而是很可能有一个逐渐变化的过程，那么在导数绝对值大处，我们不妨大胆地把步伐迈得大一些，以便更快到达最低点。