数据结构
一、数据结构
1.连续结构,数组,拿出数组某个下标的值很快,一整块区域都是它。

2.跳转结构,不是连续的,内存中分配一小块区域给a,a上面记录着值,还有一小块是记录指向下一个节点的内存地址。
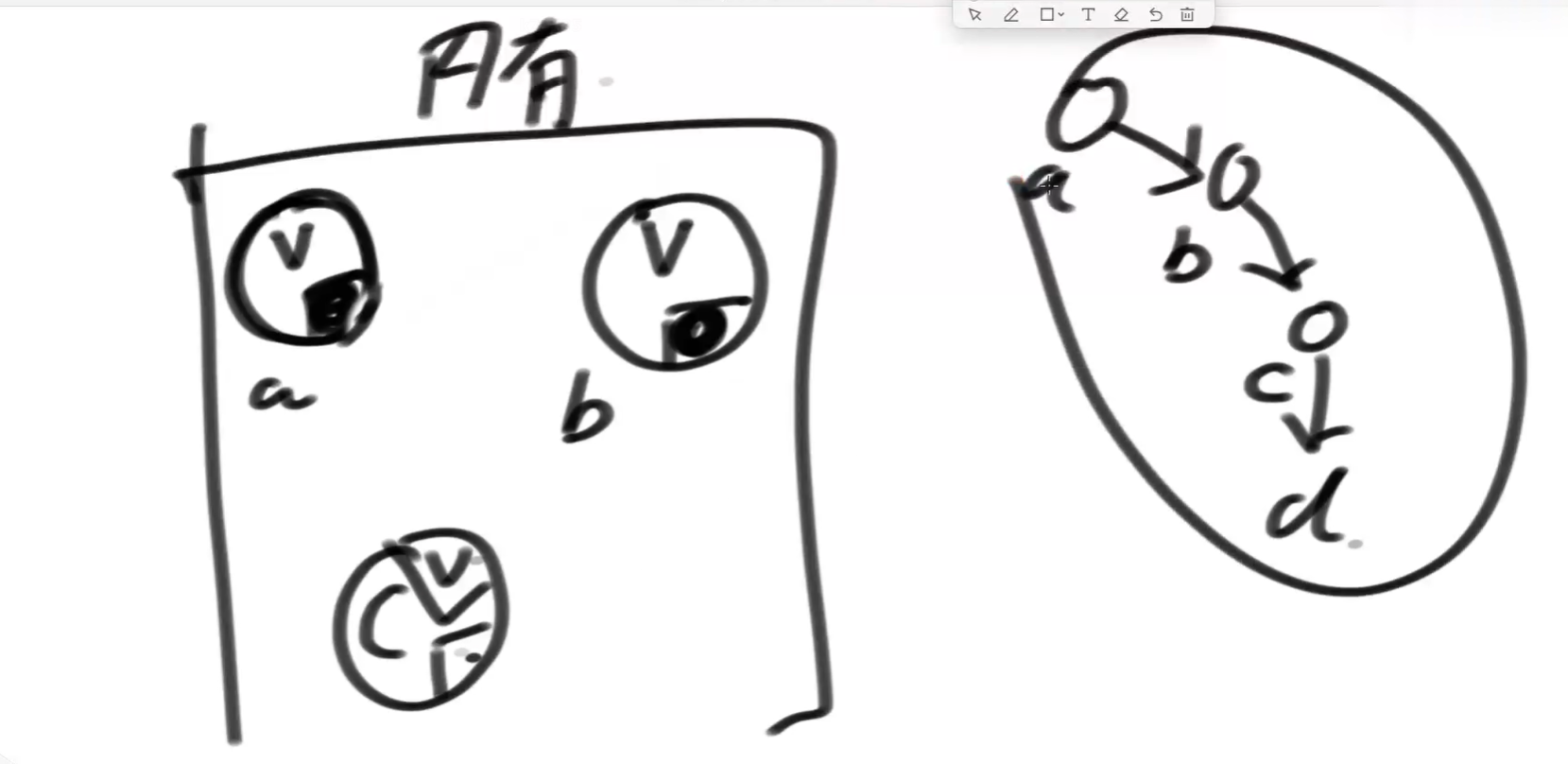
二叉树,a这个节点一小块内存,记录着值,还有两块内存记录着地址,可以想象为左指针和右指针,分别指向两个内存区域。指向下个b和c分别有各自有两块内存地址分别指向下节点...,二叉树结构就是两个跳转地址的跳转结构。
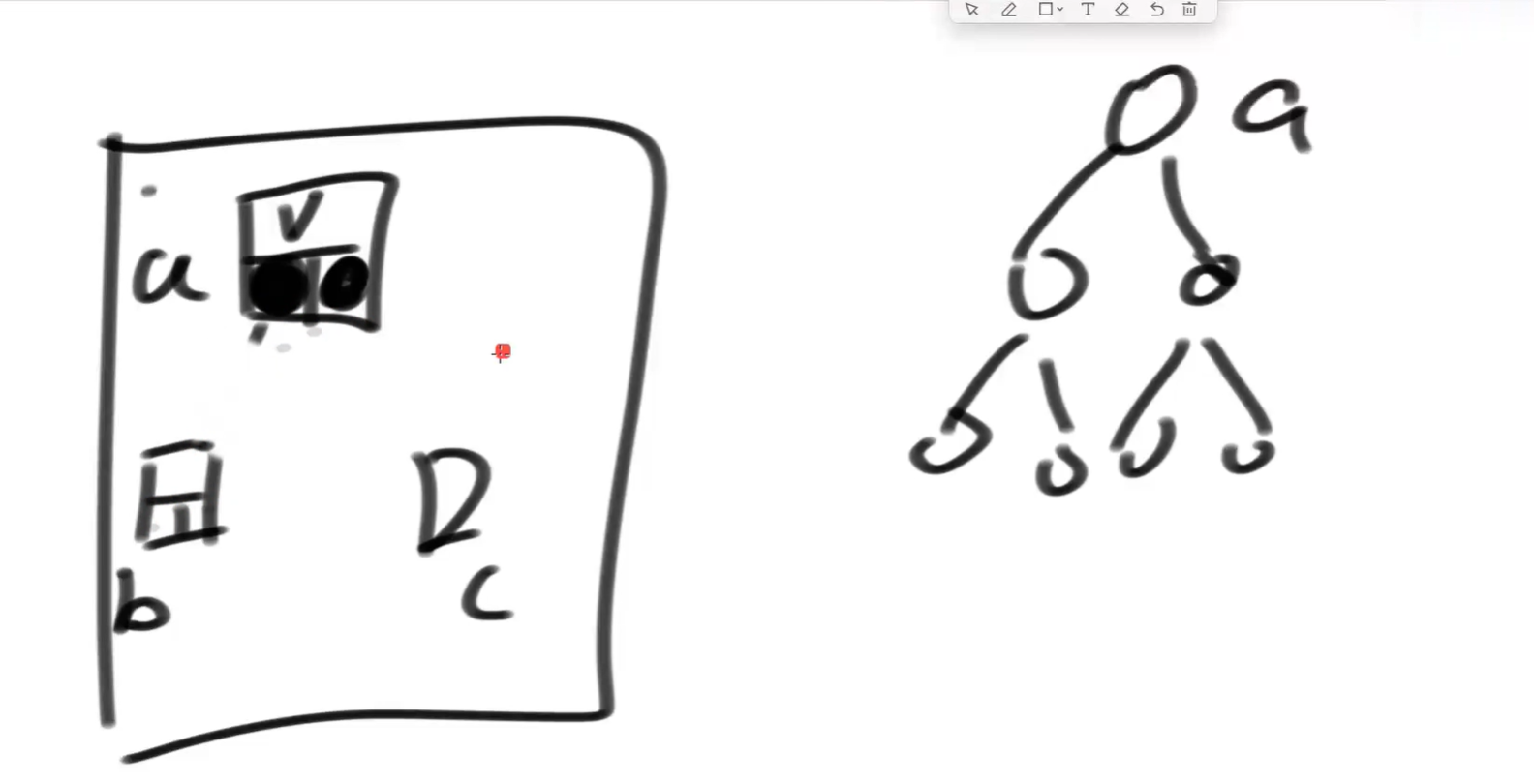
图,就是a点,往外七八条指针,a内存区域里有很多内存地址,a往外多少个分支,在内存区域里就有多少个指向地址。

所有数据结构都是连续结构、跳转结构,或者这两者拼的连续结构 + 跳转结构。
二、最基本的数据结构
1)数组
便于寻址,不便于增删数据。
比如数组里面是2,3,5,6,7,8,要把4插入到3和5之间,这对数据来说代价很高,因为它要维持自己的连续结构,只能是5,6,7,8往右边挪,腾出一个空,4插进去,很麻烦。
删除也一样。比如2,3,4,5,6,7,8,要把4删掉,5往左挪个位置把4盖掉,6,7,8都往左挪。很麻烦。
2)链表
便于增删数据,不便于寻址
比如a->b->c->d,要想在b和c中间加个e,直接e申请个内存,内存里面随便一块给我申请好,b原来的下个指针的地址不是记c的吗?改成记e就行了。e上面的内存指针下一个记c就行了。只需要改两个指针的走向,e就加进去了。其他数据根本不需要动,所以加数据很容易。
再比如a->b->e->c->d,现在要把e删掉,b原来指向e的,现在b你改成指向c就行了。e也别指向c了,内存里直接把我e释放掉就行了。
但是寻址不容易,它没有偏移量,这么一个乱七八糟的来回跳的联表,我想找到第100万个数,我怎么算偏移量啊,它在哪我都不知道,我只能一个个的数,数a是第一个,数b是第二个,数c是第三个....数到第100万个,把它拿出来,因为没有办法,他们不靠在一起,我也不知道在哪,只能这么干。
三、一个需求引发的数据结构的讨论
现在有个这样的需求:有一个数组结构,我想调用一个方法sum(arr, L, R)表示从数组中计算从下标L ~ 下标R之间的和,比如输入sum(arr, 1, 4)就是计算数组arr[1] ~ arr[4]之间的和,4 + 2 + 1 + 6,返回13,因为这个方法调用的非常频繁,几十亿次的数量级,所以如果每次调用sum方法去遍历累加计算的话,那效率不高。有没有更好的办法?
设计一个正方形的表格,长和宽为数组的长度n,为n*n的格子。每个横竖坐标对应的L,R,就是该数组对应下标的求和,把这个求和的值填在这个格子里。
如下图所示把这个表格填满。只要填满了一次,那么以后每次计算sum(arr, L, R)的值就方便了,只需要拿出对应格子的数值就可以了。
怎么做?

方案一,草图:
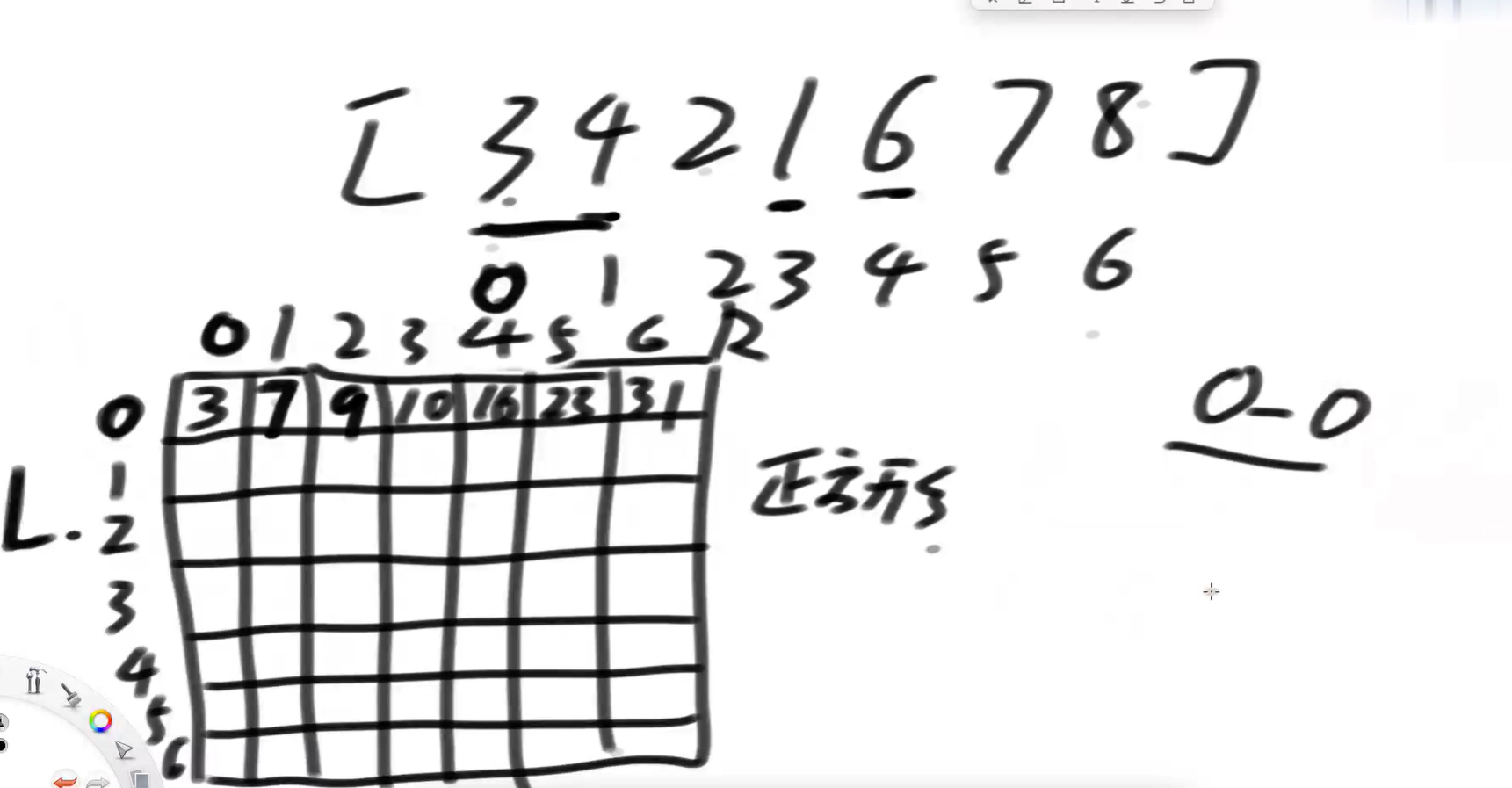
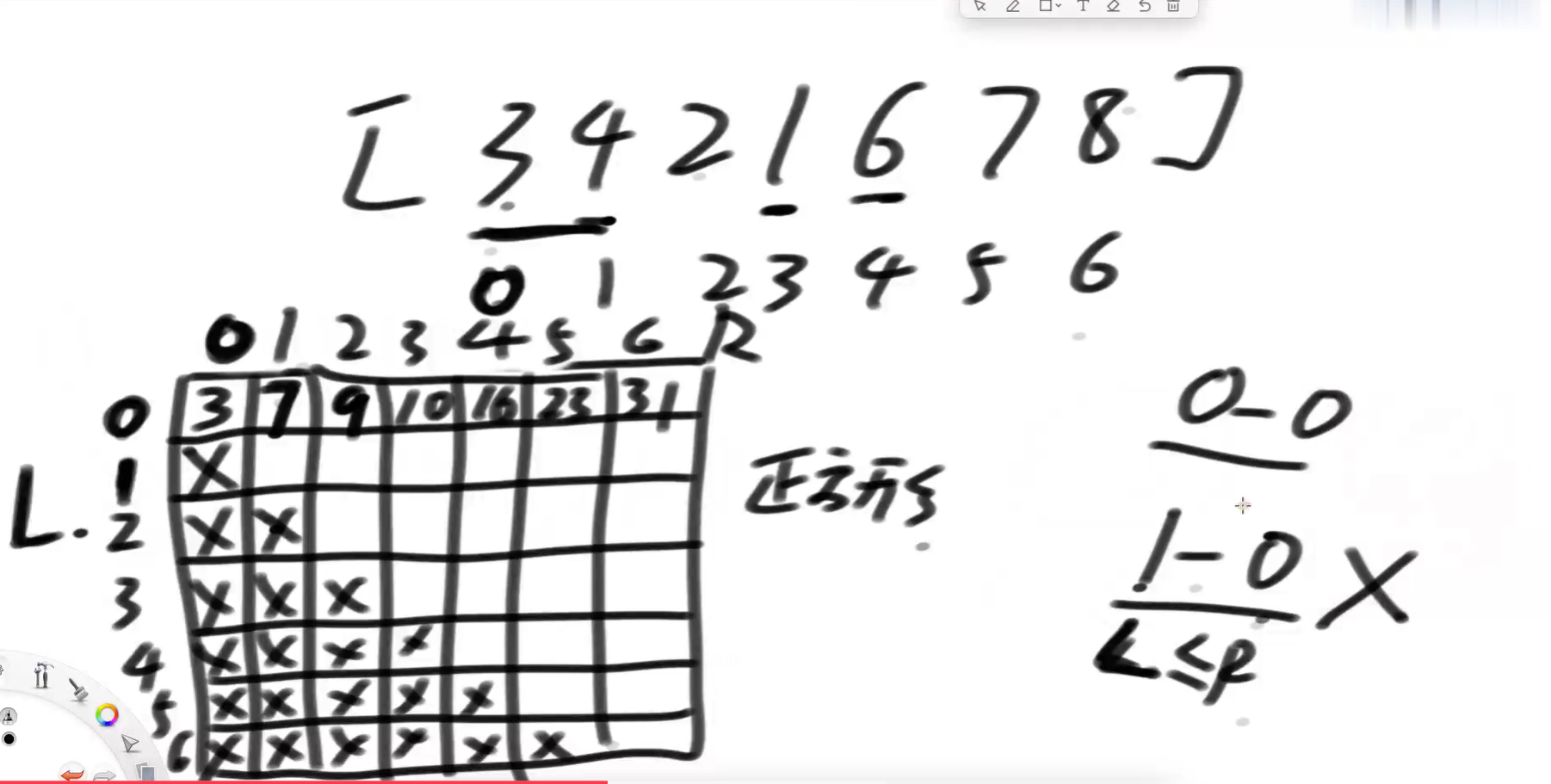


还有一种设计方案:构建help数组:

H数组表示什么含义呢?
H[i] 表示,arr[0] .. arr[i] 一路累加的整体结果
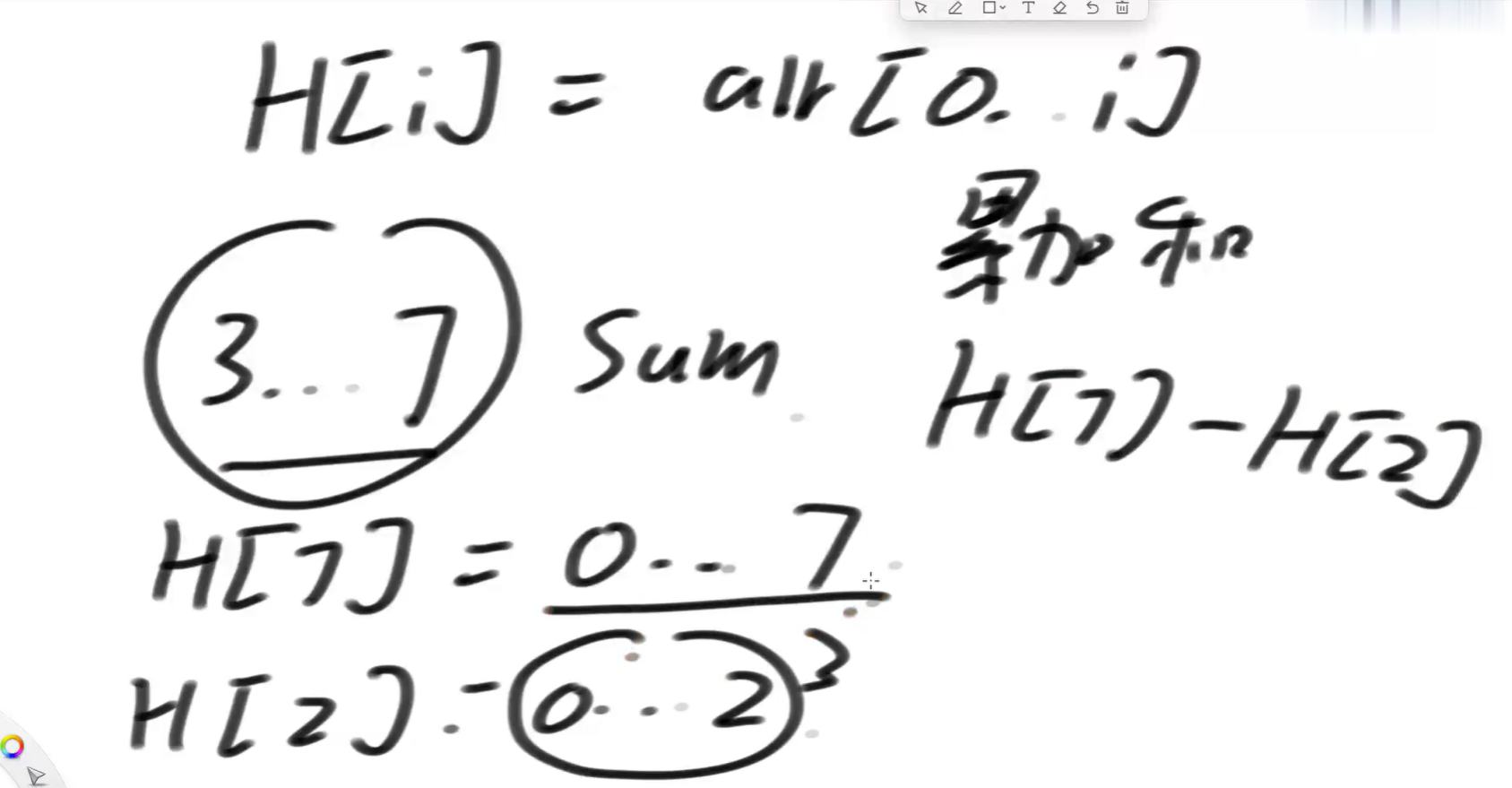
边界条件:

从节省空间上来说,第二种设计方案很巧妙,它就和原数组大小一样大就够了,而第一种设计方案需要一个正方形矩阵,可能会浪费空间。从生成时间上来说,第二种方案也好,因为它只需要遍历一遍就生成好了,以后就拿两个值一减,或者L=0的时候不用减直接返回。而第一种正方形矩阵生成的时候还需要来两个for循环的遍历。
但是要提醒大家的是,如果查询巨频繁,已经频繁到不管哪种方案生成预处理数组都无所谓的地步了,比如数组长度1000,生成正方形矩阵1000 *1000 是百万规模,但是查询十几亿,百亿次,那哪种好?
第一种好,因为第一种是直接拿值给你返回,而第二种还要减一下。所以第二种方案看起来是好,但是一旦查询量巨大无比的时候,查询次数非常非常多的时候,第一种方案其实更好。
代码实现:
package com.cy.class02;
public class Code01_PreSum {
/**
* 如果原始这么算
*/
public static class RangeSum1 {
private int[] arr;
public RangeSum1(int[] array) {
arr = array;
}
public int rangeSum(int L, int R) {
int sum = 0;
for (int i = L; i <= R; i++) {
sum += arr[i];
}
return sum;
}
}
/**
* 方案一 没有..
*/
/**
* 方案二
*/
public static class RangeSum2 {
private int[] preSum;
public RangeSum2(int[] array) {
int N = array.length;
preSum = new int[N];
preSum[0] = array[0];
for (int i = 1; i < N; i++) {
preSum[i] = preSum[i - 1] + array[i];
}
}
public int rangeSum(int L, int R) {
return L == 0 ? preSum[R] : preSum[R] - preSum[L - 1];
}
}
}四、介绍随机函数
java中的Math.random()函数
package com.cy.class02;
/**
*
*/
public class Code02_RandToRand {
public static void main(String[] args) {
System.out.println("测试开始");
/**
* Math.random() -> double -> [0, 1) 左闭右开 等概率返回一个0.几的数
* 等概率返回,看起来很神奇,因为数学上是做不到0~1等概率返回,而计算机里可以,为什么?
* 因为计算机所有的小数都是有精度的,意味着0~1之间的小数不是无穷多的,是有穷尽的
*/
int testTimes = 10000000;
int count = 0;
for (int i = 0; i < testTimes; i++) {
if (Math.random() < 0.3) {
count++;
}
}
//System.out.println("出现了"+count+"次");
System.out.println((double) count / (double) testTimes); //0.2998836
System.out.println("---------------------------------");
/**
* Math.random() * 8 之后变为:
* [0, 1) -> [0, 8)
* [0, 8)有:
* 0.x
* 1.x
* ..
* 7.x
* 所以小于4的为 0.x ~ 3.x,概率为50%
*
* 表明:Math.random() * 8之后,[0, 8)之间的数也是等概率返回
*/
count = 0;
for (int i = 0; i < testTimes; i++) {
if (Math.random() * 8 < 4) {
count++;
}
}
System.out.println((double) count / (double) testTimes); //0.4999238
/**
* Math.random() * K 转成int之后表示的数范围:
* [0, K) -> [0, K-1]
*
* counts[0]: 0出现的次数
* counts[1]:1出现的次数
* ..
* counts[8]:8出现的次数
*
* 表明:(int) (Math.random() * K)之后,[0, K-1]之间的数也是等概率返回
*/
int K = 9;
int[] counts = new int[9];
for (int i = 0; i < testTimes; i++) {
int ans = (int) (Math.random() * K); // [0, K-1]
counts[ans]++;
}
for (int i = 0; i < K; i++) {
System.out.println(i + "这个数出现了" + counts[i] + "次");
}
}
}上面代码解释草图,如何理解Math.random() * 8 < 4 出现的概率为50%:
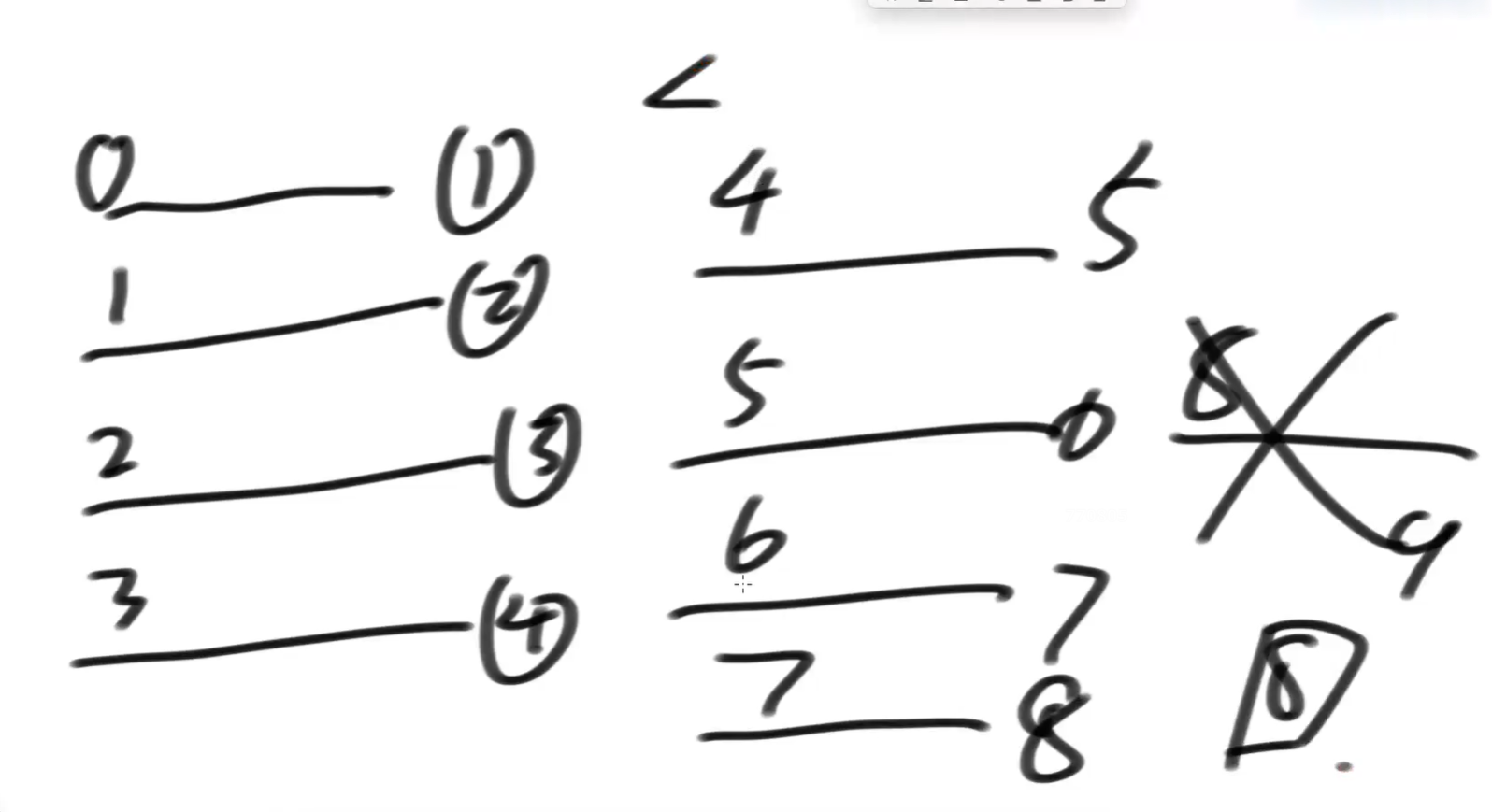
现在问题来了:我们现在知道Math.random()在[0, x)之间出现的概率为x,现在怎么让它出现x²次呢?
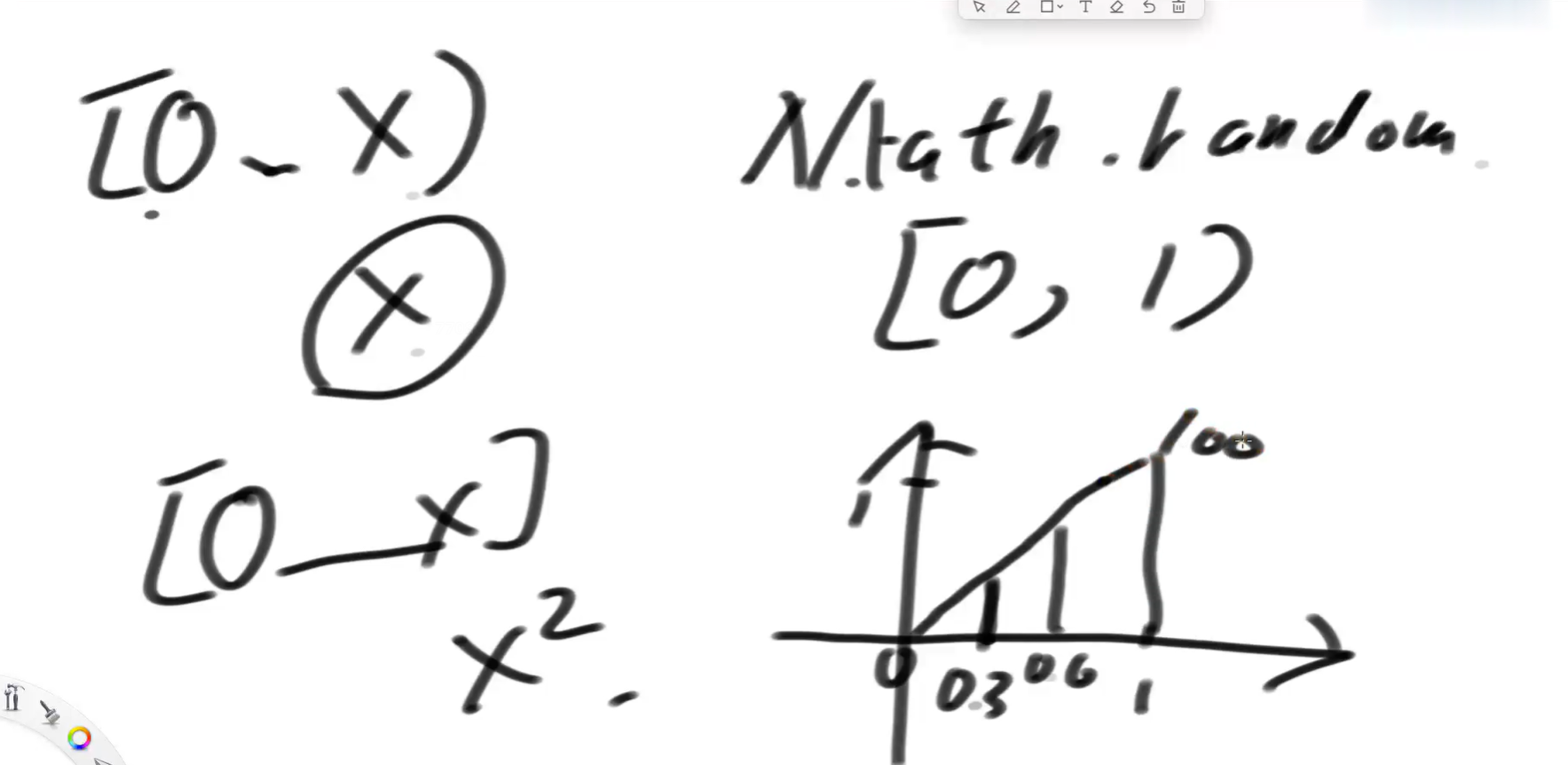
package com.cy.class02;
/**
*
*/
public class Code02_RandToRand {
public static void main(String[] args) {
System.out.println("---------------------------------");
count = 0;
double x = 0.7;
for (int i = 0; i < testTimes; i++) {
if (xToXPower2() < x) {
count++;
}
}
System.out.println((double) count / (double) testTimes);
System.out.println(Math.pow(x, 2));
System.out.println("---------------------------------");
count = 0;
x = 0.7;
for (int i = 0; i < testTimes; i++) {
if (xToXPower3() < x) {
count++;
}
}
System.out.println((double) count / (double) testTimes);
System.out.println(Math.pow(x, 3));
}
/**
* 返回[0,1)的一个小数
* 任意的x,x属于[0,1), [0,x)范围上的数出现概率由原来的x调整成x平方
*
* 怎么做到的?
* 是求最大值,max,分别调了两次随机行为,两次随机行为是独立的,怎么才能落到[0,x)范围上?
* 只有两次行为都落在[0,x)上面才能返回[0,x)上,两次都命中这个范围,最终才能返回[0,x)范围上的数,所以是x²
*/
public static double xToXPower2() {
return Math.max(Math.random(), Math.random());
}
public static double xToXPower3() {
return Math.max(Math.random(), Math.max(Math.random(), Math.random()));
}
}如果上面中的写成了Math.min(Math.random(), Math.random())呢,它在[0,x)上面出现的概率是什么?
1-(1-x)²
演算草图:
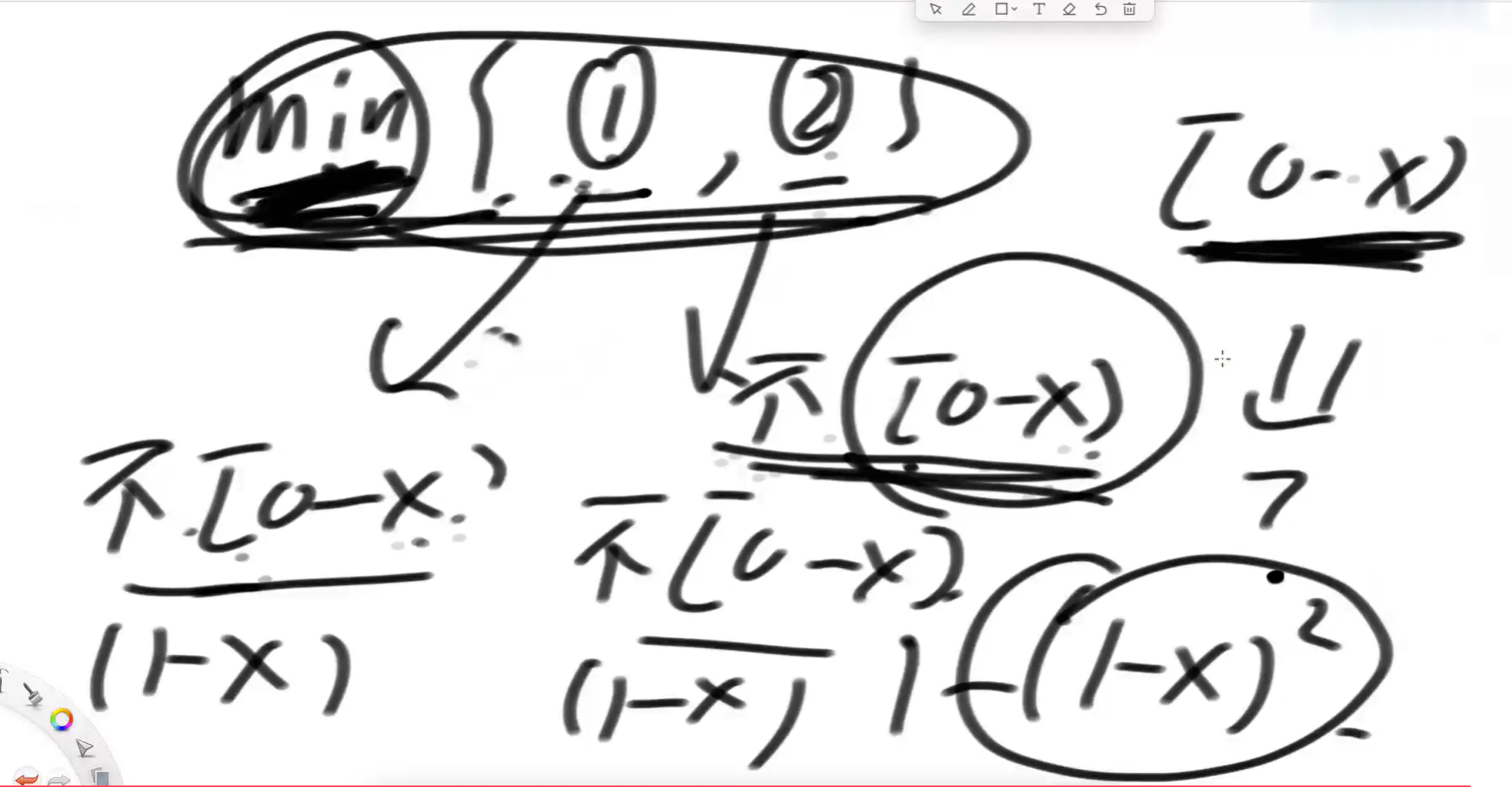
五、介绍随机函数
从1-5随机到1-7随机
从a-b随机到c-d随机
01不等概率随机到01等概率随机
需求:
假设f()可以等概率返回1-5之间的随机数。而且不能借助外力随机函数Math.random什么的,只能利用唯一的随机函数f();
在只使用f()的情况下, 如何精巧的使用f()能让1-7之间的数等概率返回?
那么我们想:可不可以让返回值+2呢?
不行,原来是1,2,3,4,5等概率返回,+2了之后只能是3,4,5,6,7等概率返回,得不到1和2等概率返回。
这样做:思路:
可不可以根据f()等概率返回1-5之间的数,能不能改造得到一个0~1之间返回的等概率发生器?比如f()得到1、2的时候我就返回0,f()得到4,5的时候我就返回1,f()得到3的时候就让f()重新来一遍,我就让f()得到1,2,4,5,其他数不让得到。这样就改造成了0,1发生器,而且是等概率的。

有同学会有疑问,为什么等于3的时候重新调用f了,最后返回0,1还是等概率的?演算草图:
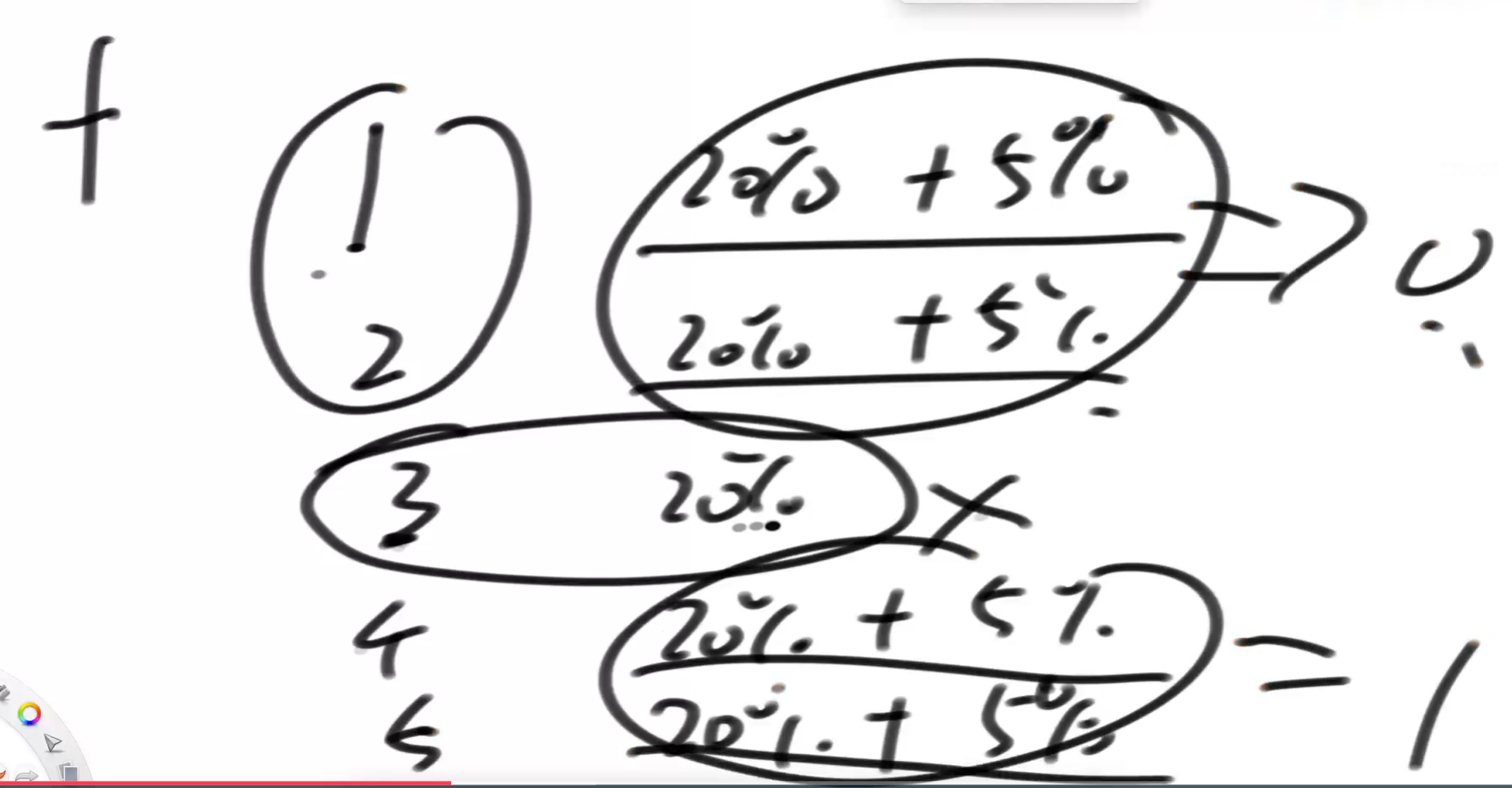
既然得到了f2()可以等概率返回0,1发生器。怎么等概率返回1~7之间的数呢?
往前推:怎么得到0~6之间等概率返回呢? 要返回1~7那就0~6再+1就行了。再想:
如果1个二进制位,可以返回0~1
如果2个二进制位,可以返回0~3
如果3个二进制位,可以返回0~7
所以返回0~6需要3个二进制位。三个二进制位上分别调用f2(),都是独立的,那么返回:
000
001
010
...
111
这些数是等概率返回的,也就是0~7一共8个数等概率返回,每个数的概率是1/8
然后遇到7就重新生成,只让他产生0~6的,那么最后就返回0~6之间的数等概率返回喽!

代码实现:
package com.cy.class02;
public class Code02_RandToRand {
public static void main(String[] args) {
// f2():0,1等概率发生器测试
int count = 0;
for (int i = 0; i < testTimes; i++) {
if (f2() == 0) {
count ++;
}
}
System.out.println((double) count / (double) testTimes);
System.out.println("---------------------------------");
counts = new int[8];
for (int i = 0; i < testTimes; i++) {
int num = f3();
counts[num] ++;
}
for (int i = 0; i < 8; i++) {
System.out.println(i + "这个数出现了" + counts[i] + "次");
}
System.out.println("---------------------------------");
counts = new int[8];
for (int i = 0; i < testTimes; i++) {
int num = g();
counts[num] ++;
}
for (int i = 0; i < 8; i++) {
System.out.println(i + "这个数出现了" + counts[i] + "次");
}
}
/**
* f1()为题目中要求的等概率随机返回1~5之间的数。
* lib中的,黑盒,不能改。只能调用。
*/
public static int f1() {
return (int) (Math.random() * 5) + 1;
}
/**
* 随机机制,只能用f1()
* 等概率返回0和1
*/
public static int f2() {
int ans = 0;
do {
ans = f1();
} while (ans == 3);
/**
* 1 2 返回0
* 4 5 返回1
* 根本没有返回3的时候
*/
return ans < 3 ? 0 : 1;
}
/**
* 得到000 ~ 111做到等概率返回
* 0 ~ 7等概率返回
*/
public static int f3() {
return (f2() << 2) + (f2() << 1) + (f2() << 0); //相当于 2² + 2¹ + 2º
}
/**
* 0~6等概率返回
* 调用f3,只要得到7就重做,保证只返回0~6
*/
public static int f4() {
int ans = 0;
do {
ans = f3();
} while (ans == 7);
return ans;
}
/**
* 1 ~ 7 等概率返回
*/
public static int g() {
return f4() + 1;
}
}推广一下,如果给定f()是3~19之间等概率返回的, 要你实现一个g()做到20~56之间等概率返回,怎么做?
1.先做f()对应的0~1之间发生器f1(),3~10返回0, 12~19返回1,11的时候重做,得到0,1发生器。(如果a~b之间的个数正好是偶数,那就不需要重做了,奇数次需要重做)
2.要20~56之间等概率返回,减去20,得到0~36之间等概率返回,结果+20就行了。
3.0~36需要6个二进制位,6个二进制位表示0~63。让f1()发生器生成6次,得到能返回0~63之间等概率返回。
4.然后当返回的数>36的时候重做。得到0~36等概率返回了。
那就上述中的 从a-b随机到c-d随机 也实现了。
01不等概率随机到01等概率随机,如何实现?
f()函数返回0的概率为P,返回1的概率为1-P;是固定概率,但是不是等概率。这个意思。怎么写出g(),等概率返回0和1?
思路:
将f做两次:
如果得到0 0 不要了,重做
如果得到1 1 不要了,重做
如果得到0 1,返回0 概率是 p * (1-p)
如果得到1 0,返回1 概率是 p * (1-p)

代码实现:
package com.cy.class02;
/**
*
*/
public class Code02_RandToRand {
public static void main(String[] args) {
/**
* x函数以0.84的概率返回0,1-0.84的概率返回1.
* 你只能知道,x会以固定概率返回0和1,但是x的内容,你看不到。
* 也就是你不知道x的内部返回0和1具体的固定概率是多少
*/
public static int x() {
return Math.random() < 0.84 ? 0 : 1;
}
/**
* 等概率返回0和1
* ans = x(); x做第一次,0或1
* ans == x() x做第二次, 0或1
* 如果第二次等于第一次的值,那就重做。
*/
public static int y() {
int ans = 0;
do {
ans = x();
} while (ans == x());
// ans 0 1
// ans 1 0
return ans;
}
}左神名言:
生活的意义不是一开始赋予的,是你付出了之后赋予的。你吃过苦你就觉得它有意义。就这么回事,虽然有点悲观主义。我是谁是我经历决定的。
--



 浙公网安备 33010602011771号
浙公网安备 33010602011771号