[技术博客] 较科学的排名算法介绍与实现

[技术博客] 较科学的排名算法介绍与实现

• [技术博客] 较科学的排名算法介绍与实现
  • 太长不看版
  • 传统常用排名算法以及它们解决我们问题的局限性
    • 平均/加权平均
    • IMDB算法（贝叶斯算法）
    • Wilson区间法
  • 几种科学的排名算法及我们的实现
    • 梅西法
      • 数学理论
      • 步骤及例子
      • 代码
    • 科利法
      • 数学原理
      • 步骤与例子
      • 代码
    • 马尔可夫法
      • 数学原理
      • 例子
    • 处理平局
    • 排名聚合
  • 算法效果
  • 其他算法
  • 我们的解决方案

我们在制作公客网项目时，有一个功能是对教师和课程的评分排名。排名这个玩意吧可以简单地加权平均分，也可以用一些复杂的方法。本文打算首先介绍一下一些常用的简单排名方法有哪些问题，接着介绍一下一些其他几种简单的科学排名算法，以及我们的Python实现，最后讲一下我们的解决方案和其他东西。

本文着重介绍的排名算法大多来自于《谁排第一？关于评价与排序的科学》一书，例子，说明和代码则是自己完成的，如有疏漏请指出，谢谢。

太长不看版

简单的方法如算术平均，加权平均是有不少漏洞和问题的。

我们介绍的算法考虑并试图解决了这些问题，更科学一些。但是人无完人，这些算法依然还是可以被针对的，只是难度大一些。

我们实现的算法的仓库在这里仓库，如果想尝试的话，看一下里面的例子应该可以很快地部署到自己的项目中。

写完以后发现有人造了一个rankit的python库，更加完善。就我们项目来说还是自己造的轮子舒服一点，因为这个库需要先把数据转成pandas的dataframe再调用，如果是新项目的话使用这个库也是更好的选择。

传统常用排名算法以及它们解决我们问题的局限性

平均/加权平均

这种算法实现快，简单，效果也凑合。这种算法的问题也不少，比如刷分问题难以杜绝，不同人评分分布不同，这个问题在评分群体少，打分目标交集少的情况尤为严重。比如我们的项目，目前阶段基本上每门课只有2~5个打分，一个高分低分对排名的影响极大。而实际上，每门课上课人数基本上只有50人左右，因此每门课的打分人数理想状态下也就是60人（考虑前几届的），群体依然较少，问题依然没有避免。

IMDB算法（贝叶斯算法）

IMDB算法的公式大概是这样：参考这个知乎问题

weighted rank (WR) = (v ÷ (v+m)) × R + (m ÷ (v+m)) × C
R = average for the movie (mean)
v = number of votes for the movie
m = minimum votes required
C = the mean vote across the whole report (currently 6.9)

简单来说就是评分人数达到一定标准才会进入排名，评分人数少但是评分高的项目会受到一些“惩罚”，最终选出的是大家都说好的东西。

但是就我们的项目而言，首先评分人数要求就难以解决，限制线低的话和平均没啥区别，限制线高的话基本没有项目满足条件。此外平均分高的时候区别度会显著降低。因此我们也没有采用这个算法。

Wilson区间法

简单来说是计算每个项目好评的置信区间进行排名，据说Reddit在用，网上找到了一个公式：

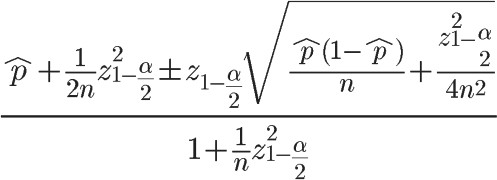
但是这个算法有一个问题就是评分人数越多的项目越容易排在前面，这样投票人数少的项目难以反超。
另外鄙人数学水平较低，本垃圾的概统是两天速成的，这公式看上去就让我兴致全无，不想实现。

几种科学的排名算法及我们的实现

我们打算介绍一下梅西法（Massey Ranking），科利法（Colley Ranking），处理平局的梅西法，科利法和排名聚合。

这些算法主要的优点是解决了一些情况下的恶意刷分以及不同人群评分标准的差异，整体来说不算十分难以理解，实现起来也不算困难，每个算法的代码行数在50行左右。

这些算法都被数学建模，BCS等体育赛事等广泛使用过。Netflix曾经采用了有平局的科利法作为排名方法，而马尔可夫法是Page Rank的原型之一。在实际应用中，我们发现马尔可夫法并不很适合我们的场景，因此我们最终没有使用。

梅西法

我们从最简单的梅西法开始。梅西法看中的是评分的分差，利用它给出不同项目的打分，进而排名。梅西法现在作为BCS评分的重要组成部分，也是Netflix曾经采用的排名方法。

数学理论

我们通过构造一个评分矩阵，来描述两个项目的优劣关系，进而做出评分。例如一个人给A打了4分，给B打了2分，那么我们构造一个列，在A位置记录一个1，B位置记录一个-1，把他放到评分矩阵里，同时记录数字的差（2）为这行的值。重复这个操作，我们就可以得到一个 （评分条数） * （项目个数） 的系数矩阵X以及一个 （评分条数） * 1 的值矩阵Y。我们可以试图找到一个XY之间的关系r，可以表示为 Xr=Y，这个r就描述了这些评分项目之间的差别。 但是显然这个方程组高度超定且矛盾，很可能没有有唯一解，因此我们通过计算 \(X^{T}Xr=X^{T}Y\) 的方式求一个最小二乘解作为最佳线性无偏估计。

步骤及例子

以上是无聊的理论部分，在实际应用中，我们做了简化来构造\(X^{T}X\)，我用一个例子来说明一下实际的算法。

我们假设有以下4个用户对3门课程打分（1-5）：

用户	A	B	C
1	5	3	X
2	5	1	2
3	1	X	X
4	X	3	4

首先我们统计一下有效的课程评分对：

#	Win	Lose	delta
1	A	B	2
2	A	B	4
3	A	C	3
4	C	B	1
5	C	B	1

这里用户3被认为是恶意刷分（事实上，如果他AB都投了1分，也会被发现是恶意刷分），而用户的打分分布（如2和4对于BC的分布）也被消除了。

然后我们按以下规定构造矩阵：

• 矩阵的主对角线上为该元素参与的评价次数
• 每有一个评价，将AB和BA位置的值减一
• 评分矩阵是每个元素的评分收益的绝对值

因此我们得到了如下的矩阵：

显然该矩阵不满秩，因此我们将最后一行（任意一行）替换，表示所有项目的Massey评价之和为0.

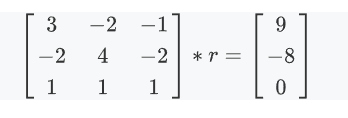
现在它满秩了，可以解了，解就是这几项的评分。

项目	Massey 评分	排名
A	1.9167	1
B	-1.3333	3
C	-0.5833	2

以上就是基础的梅西法了，在我们的实际情况中还要考虑打分相同等情况，将在后面处理平局中描述。

代码

以下是我们的实现代码：

    def massey(self) -> np.array:
        """
        The Massey Ranking.
        Returns the item name, ranking and the score.
        """
        # We first init the Massey matrix
        score_list = np.zeros(self.item_num)
        for i in self.record_list:
            if i[2] == i[3]:
                # Throw away draw games
                continue
            winner = self.all_item.index(i[0])
            looser = self.all_item.index(i[1])
            score_list[winner] += i[2] - i[3]
            score_list[looser] += i[3] - i[2]
            self.item_mat[winner][winner] += 1
            self.item_mat[looser][looser] += 1
            self.item_mat[winner][looser] -= 1
            self.item_mat[looser][winner] -= 1
        # replace the last line with 1
        self.item_mat[-1] = np.ones(self.item_num)
        score_list[-1] = 0
        # solve the matrix
        score = np.linalg.solve(self.item_mat, score_list)
        for i in range(self.item_num):
            self.ranking.append([self.all_item[i], 0, score[i]])
        self.ranking.sort(key=lambda x: x[-1], reverse=True)
        for i in range(self.item_num):
            self.ranking[i][1] = i + 1
            if i > 0 and self.ranking[i][2] == self.ranking[i - 1][2]:
                self.ranking[i][1] = self.ranking[i - 1][1]
        return self.ranking

科利法

相比于梅西法，科利法的数学推理要复杂一些，不过最终实现上难度与梅西法相当。同样的，科利法也是BCS评分的重要组成部分，Netflix也曾经采用的排名方法。

数学原理

简单来说科利法以传统的胜率模型为基础，考虑了对手的强弱来修正补偿。科利法的主要特点是它不考虑评分差距，即5-1和3-2对于其来说是一致的，都记为前者比后者好1次。这样，恶意刷分的行为就会被尽可能地消除一些，同时也避免了误伤。

科利法的得分可以由公式

\[r_{i}=\frac{1+w_{i}}{2+t{i}} \]

给出，其中 \(w_{i}\),\(t_{i}\) 为获胜场数和总场数。

在初始时所有项目的评分都是0.5，随着记录的次数增加，有的项目评分上升，有的则降低。为了方便求解，我们做了一些近似，则有：

\[\begin{aligned} w_{i} &= \frac{t_{i}-l_{i}}{2}+\frac{t_{i}+l_{i}}{2} \\ &= \frac{t_{i}-l_{i}}{2}+\frac{t_{i}}{2}\\ &\approx \frac{t_{i}-l_{i}}{2}+\sum_{j \in opponents}{r_{j}} \end{aligned} \]

这样我们就把每个项目的\(r\)与其他项目关联起来了，可以利用类似上面梅西法的矩阵求解了。同样的，我们构造一个线性方程组\(Cr=b\)，其中\(r_{n*1}\)为目标评分向量，\(b_{i}=1=0.5(w_{i}-l_{i})\)为每个项目的打分，\(C\)的主对角线上为该项目的有效评价组数+2，其余元素为对应元素的评价组数的相反数。

与梅西法不同的是，这里这个方程组是满秩的，因此我们不需要替换其中的一行。

梅西法和科利法看上去十分类似，但是他们还是略有区别的。首先，科利法不是无偏估计，此外，科利法考虑的是获胜次数而不是分差。当然还有一个结合了两种方法的科利化梅西法，这又是一种其他的算法了。

步骤与例子

我们依然以上面的例子来看一下科利法是怎么运行的。

有效的课程评分对：

#	Win	Lose	delta
1	A	B	2
2	A	B	4
3	A	C	3
4	C	B	1
5	C	B	1

然后我们按以下规定构造矩阵：

• 矩阵的主对角线上为该元素参与的评价次数+2
• 每有一个评价，将AB和BA位置的值减一
• 评分向量是该项目与其他项目比较获胜的次数

因此我们得到了如下的矩阵：

\[ \left[ \begin{matrix} 5 & -2 & -1 \\ -2 & 6 & -2 \\ -1 & -2 & 5 \end{matrix} \right] * r = \left[ \begin{matrix} 2.5 \\ -1 \\ 1.5 \end{matrix} \right] \]

解方程，就可以得到科利法的评分了。

项目	Colley 评分	排名
A	0.708	1
B	0.25	3
C	0.542	2

同样的，科利法也需要处理一下平局，我们在之后会提到这个问题。

注：书上第27页，如果我没理解错的话例子的解是有问题的。它的\(p_{4}\)好像算错了。

代码

以下是我们的实现代码：

        def colley(self)-> np.array:
        """
        The Colley Ranking.
        Returns the item name, ranking and the score.
        """
        # We first init the Colley matrix
        self.item_mat = np.zeros(shape=(self.item_num, self.item_num))
        self.ranking = []
        score_list = np.ones(self.item_num)
        for i in range(self.item_num):
            self.item_mat[i][i]=2
        for i in self.record_list:
            if i[2] == i[3]:
                # Throw away draw games
                continue
            winner = self.all_item.index(i[0])
            looser = self.all_item.index(i[1])
            score_list[winner] += 0.5
            score_list[looser] -= 0.5
            self.item_mat[winner][winner] += 1
            self.item_mat[looser][looser] += 1
            self.item_mat[winner][looser] -= 1
            self.item_mat[looser][winner] -= 1
        # solve the matrix
        score = np.linalg.solve(self.item_mat, score_list)
        for i in range(self.item_num):
            self.ranking.append([self.all_item[i], 0, score[i]])
        self.ranking.sort(key=lambda x: x[-1], reverse=True)
        for i in range(self.item_num):
            self.ranking[i][1] = i + 1
            if i > 0 and self.ranking[i][2] == self.ranking[i - 1][2]:
                self.ranking[i][1] = self.ranking[i - 1][1]
        return self.ranking

马尔可夫法

虽然我们最后没有采用这种算法，但是也还是介绍一下。马尔可夫法是Page Rank的模型之一，也有很多变种，主要是投票的形式不同，差距也比较大。无法找到一个合适的投票方式也是我们没有采用它的原因之一。

数学原理

正如其名，马尔可夫法的核心是马尔科夫链，就是那个概统里面最简单的送分大题。简单来说，马尔可夫法描述的是一个利益无关的人，按照马尔科夫链随机在目标之间移动，最后统计一下它处于每个目标的时间（次数），就是这些项目的评分了。即求\(Cr=r\)中的\(r\)。可以看出算法的关键是马尔科夫链的构造，这里主要是一个投票模型，有以下几种常见的投票方法：

• 输家向赢家投1票
• 输家向赢家投对方评分票
• 两家各项对方投对方评分票

整个算法的流程是：投票->根据结果构造马尔科夫链->计算稳态向量

例子

我们还是通过上面的那个例子看一下这个算法。这里我们采用的是互相投对方评分票。每进行一次投票就相当于\(C_{i,j}+=s_{i},C_{j,i}+=s_{j}\)

还是刚才的例子：

用户	A	B	C
1	5	3	X
2	5	1	2
3	1	X	X
4	X	3	4

经过投票，我们可以得出：

\[ C=\left[ \begin{matrix} 0 & 4 & 2 \\ 10 & 0 & 6 \\ 5 & 4 & 0 \end{matrix} \right] \]

然后我们进行归一化：

\[ C'=\left[ \begin{matrix} 0 & \frac{4}{6} & \frac{2}{6} \\ \frac{10}{16} & 0 & \frac{6}{16} \\ \frac{5}{9} & \frac{4}{9} & 0 \end{matrix} \right] \]

这里有一个特殊情况，如果某一行全部是0的话（表示没有人给他投票），我们把这一行处理成全部是1/n，类似Page Rank的悬挂节点，表示这个项目比较优秀，我们可以随机另外选一个点重新开始。

我们的目标是求\(C'\)的稳态向量，通过查阅概统书和线代书，一般的求法是通过求特征值与特征向量，在构造向量积进行计算。具体来说，就是求\(|\lambda E-C|=0\)中的\(\lambda\)。利用性质可以知道有一个解是1，另外两解可以根据行列式和CASIO较轻松的计算出。然后我们再计算特征向量。。。

当然，我们也有其他算法。利用马尔可夫链特性和条件有比较简单的做法。我们可以通过\(Cr=r\)硬解，即C左乘r的值不变列方程。经过简单计算，我们有

\[\begin{aligned} Mr &=0 \\ 其中 M &= C'^{T}-E \\ &= \left[ \begin{matrix} -1 & \frac{10}{16} & \frac{5}{9} \\ \frac{4}{6} & -1 & \frac{4}{9} \\ \frac{2}{6} & \frac{6}{16} & -1 \end{matrix} \right] \end{aligned} \]

显然，\(M\) 不满秩。我们依然采用梅西法中用过的小技巧，将最后一行都换成1，此时方程变为：

\[ \left[ \begin{matrix} -1 & \frac{10}{16} & \frac{5}{9} \\ \frac{4}{6} & -1 & \frac{4}{9} \\ 1 & 1 & 1 \end{matrix} \right] * r = \left[ \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \right] \]

现在可以解了，解出：

项目	Markov 评分	排名
A	0.373	1
B	0.365	2
C	0.261	3

然而，使用只投一票的方式，接触的结果是：

项目	Markov 评分'	排名
A	0.632	1
B	0.053	3
C	0.316	2

评分差距较大，而且还有许多其他投票方式，我们一时没有搞懂应该采用哪一种，因此我们就没有采用Markov法。

我们也对此进行了调查，其实在书的13章有提到，马尔可夫法对于评分组中的小秩改变十分敏感，而我们的样例数据比较小，造成了结果的波动相当大。而梅西法和科利法对秩改变敏感性较低，能对这种数据容错。

处理平局

由于我们采取的是五分制打分，平局实际上是非常常见的情况。如果简单地扔掉平局的话一是会导致大量数据被浪费，另外还会导致实际的样本非常少。在这里，我们参考了Netflix当年的解决方案，对于两种算法，我们将每一个平局，例如给AB都投了3分，分解成两组：A3.5，B2.5和A2.5,B3.5都加入计算。

我们也增加了一个方法处理这个过程，该方法会扫描读入的记录，找出平局并在最后加上两组记录。

    def find_dup(self) -> None:
        for i in self.record_list:
            if i[2] == i[3]:
                self.record_list.append([i[0], i[1], i[2] + 0.5, i[2] - 0.5])
                self.record_list.append([i[1], i[0], i[2] + 0.5, i[2] - 0.5])

排名聚合

我们前面介绍了两种科学的排名方法，而在实际应用中，显然没有什么网站会显示两种不同的排名的。为此，我们采取了排名聚合的方式，将两个排名综合起来。我们采取了波达计数的方式进行排名。简单来说，就是将不同排名方法的名次取和作为总名词的比较因素。值得注意的是，波达计数的输入排名序列中的内容可以是不同的，比如A课程只在平均法中出现而B课程在平均法和梅西法中都出现了。一般来说，我们会给A课程一个模拟的梅西法排名，可以取最后或者中位值。在实际应用中，我们给A课程增加了中位值作为虚拟排名。代码如下：

    """
        borda merge
        Input example:
        [
        [['A',3],['B',1],['D',2]],
        [['A',2],['B',1],['D',4],['C',3]],
        ]
        :param ranks: A list of items and their rank.
        :return: the merged ranking list
        """
        # first get all items
        all_item=[]
        scores=[]
        length_of_rank=[]
        for i in ranks:
            length_of_rank.append(len(i))
            for j in i:
                if not j[0] in all_item:
                    all_item.append(j[0])
        for i in all_item:
            scores.append([i])
            for j in range(len(length_of_rank)):
                scores[-1].append(-1)
        # Do broda count
        for i in range(len(ranks)):
            for j in range(len(ranks[i])):
                scores[all_item.index(ranks[i][j][0])][i+1]=ranks[i][j][1]
            # add unranked items
            for j in range(len(all_item)):
                if scores[j][i+1]==-1:
                    scores[j][i+1]=0.5*length_of_rank[i]+0.5
        borda=[]
        for i in scores:
            borda.append([i[0],sum(i[1:]),0])
        borda.sort(key=lambda x:x[1],reverse=False)
        for i in range(len(borda)):
            borda[i][2] = i + 1
            if i > 0 and borda[i][1] == borda[i - 1][1]:
                borda[i][2] = borda[i - 1][2]
        return borda

算法效果

介绍完了这些科学的排名方法，我们再用一个例子来说明为什么这些排名方法更好。下面的例子部分出自我们网站数据库中的一些打分：

	课程A	课程B	课程C	课程D
a	5	3	X	X
b	3	2	X	2
c	5	X	3	4
d	X	X	5	X
e	X	X	5	5
f	X	5	5	4

	平均分	Massey	Colley	borda
a	2	1	1	1
b	4	2	2	2
c	1	4	3	3
d	3	3	4	3

可以看到排名上有较大的差距。事实上，由于abc，def分属两个不同的群体，他们的打分标准不一致，def的平均给分更高，这可以从公共课CD上看出来。使用平均值的方法就会导致这个问题。

对于有人恶意评分的情况，显然假设有一个人恶意给一门课，假设为D刷分，如果他只给D打分的话，他的打分实际上是不会计入梅西法或者科利法的（因为不存在评分对），对我们的打分没有影响。而简单平均值法就没有办法防范这种类型的攻击。

对于一个较复杂的情况，比如有人恶意刷分，给A课程打1分，D课程打5分，这种情况对于我们是有一定影响的，我们也分析了一下影响。由于6人样本较小，我们假设有60个人进行了上述打分（每种10个），接着逐个增加刷分的，看看有什么影响。我们只记录了临界变化。

刷分人数 / 排名	0	3	15	25	+INF
课程A	1	1	1	1	2
课程B	2	2	3	3	2
课程C	3	4	3	3	2
课程D	3	3	2	1	1

可见，想要刷分需要有42%的用户投极端票才行。如果有半数的人都这么认为的话，这显然已经不能算是刷分，而是这门课确实出了什么问题吧。

我们再看看简单平均值的表现，我们对于课程BC进行刷分：

| 刷分人数 | 排名 | 0 | 2 | 3 | 10 | 11 |
|----|-------|-------|------|----|------|
| 课程A | 2 | 1 | 1 | 1 | 1 |
| 课程B | 4 | 4 | 4 | 3 | 2 |
| 课程C | 1 | 1 | 2 | 2 | 4 |
| 课程D | 3 | 3 | 3 | 3 | 3 |

显然，刷分的影响十分巨大，仅仅6%的恶意评分就能让原来的第一变成最后。

但是这些算法也不是万无一失的，当然也会有很多专门针对性的手段找出算法的漏洞，但总的来说，这些算法是更加科学的。

其他算法

当然，排名算法还有许多其他更好更优秀的，我们采用的仅仅是最简单的。复杂一点的有基纳法，马尔可夫法等等，Netflix现在采用的是一种分组对抗算法，以及一些learning to rate的机器学习算法。但是我们目前水平有限并且比较懒，因此暂时没有考虑实现那些算法。

我们的解决方案

目前我们采用有平局的梅西法和科利法的波达计数作为课程主排名。对于其他课程（例如某个人只投了这门课），我们仍然采用算术平均值，并将其加在上面排名之后（相当于将主排名和这些课程又做了一个波达计数）。